Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ji, Lizhen
2008.
The integral Novikov conjectures for linear groups containing torsion elements.
Journal of Topology,
Vol. 1,
Issue. 2,
p.
306.
Dranishnikov, Alexander
and
Sapir, Mark
2011.
On the dimension growth of groups.
Journal of Algebra,
Vol. 347,
Issue. 1,
p.
23.
Guentner, Erik
Tessera, Romain
and
Yu, Guoliang
2012.
A notion of geometric complexity and its application to topological rigidity.
Inventiones mathematicae,
Vol. 189,
Issue. 2,
p.
315.
Dranishnikov, Alexander
and
Zarichnyi, Michael
2014.
Asymptotic dimension, decomposition complexity, and Haver's property C.
Topology and its Applications,
Vol. 169,
Issue. ,
p.
99.
Kawamura, Kazuhiro
2014.
Recent Progress in General Topology III.
p.
639.
Yu, G.
2019.
The Novikov conjecture.
Russian Mathematical Surveys,
Vol. 74,
Issue. 3,
p.
525.
Xie, Zhizhang
and
Yu, Guoliang
2019.
Advances in Noncommutative Geometry.
p.
691.
Yu, Guoliang
2019.
Гипотеза Новикова.
Успехи математических наук,
Vol. 74,
Issue. 3(447),
p.
167.
Chung, Yeong Chyuan
2021.
Dynamical complexity and K-theory of Lp operator crossed products.
Journal of Topology and Analysis,
Vol. 13,
Issue. 03,
p.
809.


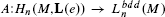 is an isomorphism. Our result is inspired by the coarse Baum-Connes results of Yu and the development of squeezing structures.
is an isomorphism. Our result is inspired by the coarse Baum-Connes results of Yu and the development of squeezing structures.