We introduce cohomologically triangulated categories as triples (A,t,▽) given by an additive category A, an additive equivalence t:AA and a cohomology class ▽ in the translation cohomology H3(A,t). A stable homotopy theory C with A = HoC yields such a triple and the class of distinguished triangles in A is deduced from ▽.

We show that the Fibered Isomorphism Conjecture (FIC) of Farrell and Jones corresponding to the stable topological pseudoisotopy functor is true for fundamental groups of a large class of 3-manifolds. We also prove that if the FIC is true for irreducible 3-manifold groups then it is true for all 3-manifold groups. In fact, this follows from a more general result we prove, namely we show that if the FIC is true for each vertex group of a graph of groups with trivial edge groups then the FIC is true for the fundamental group of the graph of groups. This result is part of a program to prove the FIC for the fundamental group of a graph of groups where all the vertex and edge groups satisfy the FIC. A consequence of the first result gives a partial solution to a problem in the problem list of R. Kirby. We also deduce that the FIC is true for a class of virtually P D3-groups.

Another main aspect of this article is to prove the FIC for all Haken 3-manifold groups assuming that the FIC is true for B-groups. By definition a B-group contains a finite index subgroup isomorphic to the fundamental group of a compact irreducible 3-manifold with incompressible nonempty boundary so that each boundary component is of genus ≥ 2. We also prove the FIC for a large class of B-groups and moreover, using a recent result of L.E. Jones we show that the surjective part of the FIC is true for any B-group.

This article has two purposes. In [15] we showed that the FIC (Fibered Isomorphism Conjecture for pseudoisotopy functor) for a particular class of 3-manifolds (we denoted this class by C) is the key to prove the FIC for 3-manifold groups in general. And we proved the FIC for the fundamental groups of members of a subclass of C. This result was obtained by showing that the double of any member of this subclass is either Seifert fibered or supports a nonpositively curved metric. In this article we prove that for any M ε C there is a closed 3-manifold P such that either P is Seifert fibered or is a nonpositively curved 3-manifold and π1(M) is a subgroup of π1(P). As a consequence it is obtained that the FIC is true for any B-group (see definition 4.2 in [15]). Therefore, the FIC is true for any Haken 3-manifold group and hence for any 3-manifold group (using the reduction theorem of [15]) provided we assume the Geometrization conjecture. The above result also proves the FIC for a class of 4-manifold groups (see [14]).

The second aspect of this article is to relax a condition in the definition of strongly poly-surface group ([13]) and define a new class of groups (we call them weak strongly poly-surface groups). Then using the above result we prove the FIC for any virtually weak strongly poly-surface group. We also give a corrected proof of the main lemma of [13].

Given a group, it is a basic problem to determine which manifolds can occur as a fixed-point set of a smooth action of this group on a sphere. The current article answers this problem for a family of finite groups including perfect groups and nilpotent Oliver groups. We obtain the answer as an application of a new deleting and inserting theorem which is formulated to delete (or insert) fixed-point sets from (or to) disks with smooth actions of finite groups. One of the keys to the proof is an equivariant interpretation of the surgery theory of S. E. Cappell and J. L. Shaneson, for obtaining homology equivalences.

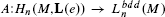We provide a bounded rigidity result for uniformly contractible manifolds with bounded geometry and sufficiently slow asymptotic dimension growth. This notion of asymptotic growth is a generalization of Gromov's definition of asymptotic dimension. In particular for these manifolds we prove that the bounded assembly map is an isomorphism. Our result is inspired by the coarse Baum-Connes results of Yu and the development of squeezing structures.

We present the first range result for the total K-theory of C*-algebras. This invariant has been used successfully to classify certain separable, nuclear C*-algebras of real rank zero. Our results complete the classification of the so-called AD algebras of real rank zero.

We give stronger counterexamples to a conjecture of Beilinson.

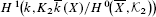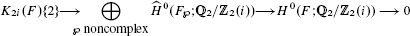
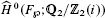Let k be a number field and let X be a smooth, projective and geometrically integral k-variety. We show that, if the geometric Néron-Severi group of X is torsion-free, then the Galois cohomology group is finite. Previously this group was only known to have a finite exponent. We also obtain a vanishing theorem for this group, showing in particular that it is trivial if X belongs to a certain class of abelian varieties with complex multiplication. The interest in the above cohomology group stems from its connection to the torsion subgroup of the Chow group CH2(X) of codimension 2 cycles on X. In the last section of the paper we record certain results on curves which must be familiar to all specialists in this area but which we have not formerly seen in print.

Let F be a real number field with r1 real embeddings. In this paper, we prove that the sequence

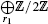is a complex, where are the Tate cohomology groups. Moreover if i ≡ 0, 1, or 2 (mod 4), then it is exact; if i ≡ 3 (mod 4), then the homology group at the second term of this complex is isomorphic to .