An expression for optimum bridge parameters is derived for a thermistor in a Wheatstone bridge and numerical values are assigned to determine the useful limits of resistance bridges tor thermistor measurements. Several digital ohmmeters are evaluated as measuring devices and are shown to compare unfavourably with a simple bridge and null detector.

Temperatures have been measured in a 299 m bore hole that reaches the base of the ice near the divide of the main ice cap on Devon Island in the Canadian Arctic Archipelago. Temperature ranges from — 23.0°C at a depth of 20 m to — 18.4°C at the bottom. The difference between surface and bottom temperatures is about 1.5 deg less than expected for a steady state. Recent climatic warming seems the most likely explanation of the discrepancy. The temperature gradient in the lowest 50 m is approximately linear and corresponds to a geothermal heal flux of 1.5 h.f.u. This value may be invalid, however, because temperatures at and below this depth have probably been perturbed by changes of surface temperature during the past several thousand years, particularly by the warming at the end of the last glaciation. A detailed analysis of the results is in progress.

The waste disposal in an ice sheet need not rely on storage periods longer than some hundreds of years. Three hundred years after dumping, the radioactive power of the fission products has decreased to about 10-4 times the value of two-year-old waste. Six hundred years after dumping, it has decreased to about 10-6 times the two-year value. There are only four radioactive fission.isotopes with half-lives between six years and 60000 years: 85Kr (10 years) has practically disintegrated after 300 years. 90Sr (with its daughter 90Y) and 137Cs (both 30 years) are reduced to 10-3 after 300 years and to 10-6 after 600 years. 151Sm (85 years) has an extremely low disintegration energy; the waste contains only a very small percentage of this isotope.

Radiation and thermal power of all fission products with long half-lives (more than 60 000 years) are many orders of magnitude smaller than those of all other fission products in waste that has been stored for several years. Furthermore, long-lived fission products have almost no radiation other than β-radiation. Future research is necessary as to whether and to what extent such long-lived isotopes, and possibly other isotopes (c.g. 239Pu or 14C), have to be separated and as to how it could be done in the safest and most economical way. The technology of separating and recycling 239Pu, an extremely valuable fissionable fuel, is being developed in view of the increasing importance of breeder reactors. The separate disposal of long-lived isotopes would not raise serious thermal or handling problems; for example, they could be deposited in a highly concentrated form into a deep geological formation

Should the waste be retrievable or not? That is ultimately a philosophical question. Which is more reliable, man or Nature? Should we trust that our descendants will have sufficient knowledge and goodwill to keep the waste safe and not misuse it—or should we rely more on Nature not to bring the waste into the biosphere by unexpected catastrophic events ?

The proposed ice-sheet disposal—be it in deep ice layers or near the surface—avoids the main dangers of both aspects. Under normal glaciological conditions the waste containers are practically irretrievable from the beginning (deep-layer deposit) or after some centuries (near-surface deposit). If, however, a catastrophic climatic change should melt away the ice sheets very quickly, the ablation melts off one after the other of the upper layers while the deep layers still remain cold. Under these circumstances the containers are “self-retrieving”: they come to the surface of (the ice or of the ice-freed bedrock and can easily be picked up. Further research on such a melt-out process and on the durability of the waste containers and their solidified contents should be carried out.

The equation governing the growth or decay of a temperature perturbation T’ in an ice slab under shear stress σxy is

where K and k are respectively the thermal conductivity and diffusivity of ice, KB-v is the advection velocity normal to the bed and

is the rate of increase of strain heating with temperature assuming a power law for flow. For a slab of infinite thickness under constant stress and at constant ambient temperature, T Fourier analysis gives -k2+a/k < o as the condition for stability where k is the wave number of a sinusoidal perturbation. When the slab has finite thickness the stability depends on the sign of the eigenvalues λm of the perturbation equation and on the boundary condition at the ice-rock interface. In general the eigenfunctions and eigenvalues must be found by approximate methods such as the Rayleigh-Ritz procedure but in the case where the stress and ambient temperature are constant over the slab thickness and there is no advection the eigenfunctions are either sines or cosines depending on the boundary conditions.

In this special case the stability condition is

if the bed is frozen and

if it is at the melting point. The eigenvalue associated with the smallest value of m is the least stable so the maximum stable thickness is thus h = ½ π(a/K)1/2 if the bed is frozen or h = π (a/K)1/2 if it is at the melting point. For typical flow-law parameters these depths are around 250 m and 500 m respectively. The eigenvalues are related in a simple way to the growth or decay rates of the eigenfunctions: (K λm)–1 is the time constant for the mth eigenfunction.

Depth-dependent stress, temperature, and advection have a marked effect on stability. A slab in which stress and temperature increase to values B and TB at the bed is considerably more stable than a slab held at constant stressσB and a constant temperature TB. Advection normal to the bed also has a major influence on stability. If the advection velocity is taken to vary linearly with depth and the bed is frozen, the effect of upward advection is to decrease stability and of downward advection to increase it. When the bed is temperate the effect of advection is more complex: downward advection increases stability but upward advection may increase or decrease it depending on the magnitude of the advection velocity.

We are interested in studying the processes of sliding of ice over a variety of rock surfaces with the object of determining an empirical relation for the basal shear stress appropriate for glaciers. The variables to be considered include: normal stress Ν, shear stress Ƭ, surface roughness r, sliding velocity V, temperature θ, water at the interface, and the presence of debris. The roughness is considered to be a function of two variables; the scale or wavelength λ, and the shape or slope of the roughness a / λ, where ais the amplitude of the variations of that scale.

It is now practicable to construct complete three-dimensional primitive- equation models of ice flow in which all the input may be time dependent. The input consists of bedrock and ocean distribution, accumulation net balance, ice-surface elevation- temperature relation, and the thermal and flow parameters of the ice. The main limitations on this type of model is the extensive demand of computation time. Thus simplified two-dimensional models have been developed for detailed flow-line studies, and single-column models have been used extensively for analysing the few deep bore-hole temperature profiles.

The main feature of the measured temperature profiles reflect the current steady-state regime at each location. Deviations from the steady state are caused by time variations of any of the variables such as surface temperature, accumulation rate, ice thickness, velocity, etc.

Measurements of stable-isotope ratios in the ice cores provide an indication of past temperatures which has been confirmed by the analysis of the temperature profiles. However the temperature changes could be either due to surface elevation changes or climate changes. Gas volumes in the core show promise of providing an indication of past elevations. Annual variations of the isotopes give indications of past accumulation rates. The determination of past velocities, however, requires velocity-temperature coupled models with more precise flow-law information.

Three-dimensional models are necessary to study past variations of the flow-line pattern. Finally the sliding and surging models recently developed need to be incorporated into the cold ice-sheet models.

Extensive glaciological studies on the Amery Ice Shell have been conducted since 1962 by the Australian National Antarctic Research Expeditions (ANARE). Deep core drilling to the depth of 310 m was carried out in 1968 at the site GI on the shell in order to obtain the vertical ice temperature distribution and to collect ice cores over the whole depth of the bore hole. General core analyses have been conducted since 1970 under an Australia- Japan Cooperative Project in order to clarify the structure of the ice shelf in connection with its flow.

It was found through these analyses that the Amery Ice Shelf consists of three layers of different origin, which are denoted the top, middle, and bottom layers. The top layer is formed by the in situ accumulation of snow on the shelf, the middle layer is glacier ice flowing from the Lambert Glacier, originating far inland on the Antarctic ice sheet, and the bottom layer is developed by the freezing of sea-water at the bottom surface. Numerical calculations were made of the formation processes of the three-layered structure of the ice shelf, in which the accumulation and the densification of snow at the top surface, the straining of the shelf, and the freezing of sea-water at the bottom surface were taken into account.

The thicknesses of the top and the bottom layers at site G1 obtained from the present calculations agree well with (hose obtained from the core analyses. The freezing rate of seawater at the bottom surface of the ice shelf estimated from the temperature profile is approximately 0.5 m a-1. This considerable growth of frozen sea-water at the base of the ice shelf results in water flowing out from under the ice shelf being more saline and warmer than that flowing in.

Forty years ago, Ahlmann considered the thermo-physical character of ice masses as a basis for differentiating glaciers into two broad geophysical groups: (1) polar and (2) temperate. About the same time, Lagally sub-divided glaciers into corresponding thermodynamic categories: (1) kalt and (2) warmen. By this it was understood that the temperature of a polar, or “cold”, glacier was perennially sub-freezing throughout, except for a shallow surface zone which might be warmed for a few centimeters each year by seasonal atmospheric variations. Conversely, in a temperate, or “warm”, glacier, the temperature below a recurring winter chill layer was consistently at the pressure melting point. As these terms are thermodynamic in connotation, glaciers of the polar type may exist at relatively low altitudes if their elevations are sufficiently great. Temperate glaciers may be found even above the Arctic Circle at elevations low enough that chilling conditions are not induced by the lapse rate.

In these distinctions, it is implied that regardless of geographical location a glacier’s mean internal temperature represents an identifiable characteristic which can be shown critically to affect the mass and liquid balance of ice masses and significantly to relate climatic influences to glacier regimes. The importance of these implications, and the fact that they are based on a gross, sometimes changing, and always difficult to measure, thermo-physical characteristic, makes some explicit terminology desirable.

To some extent Ahlmann addressed this problem by introducing a subordinate classification, sub-polar glaciers. In these, the penetration of seasonal warmth involved only a shallow surface layer at 0°C, but still to a depth substantially greater than the superficial warming experienced in summer on polar glaciers. Lagally also recognized an intermediate type which he called “transitional”, characterized by a relatively deep penetration of 0°C englacial conditions during the summer. These pioneering efforts reflect Ahlmann’s experience with glaciers in the high Arctic and Lagally’s with the Alpine glaciers of southern Europe. Although some confusion has resulted from alternate application of these different terms, both definitions can be useful. Further to refine the classification, a modified terminology is suggested by the writer. This involves introducing a fourth category, substituting the term sub-temperate for Lagally's “transitional” type on the basis that it is etymologically more consistent with the Ahlmann terminology which has remained most commonly in use. Thus, two distinct transitional categories are identified. These categories, sub-polar and sub-temperate, typify ice sheets during changes from fully polar to fully temperate englacial conditions—a situation pertaining during the waning and waxing stages of deglaciation and reglaciation,

A review of the literature reveals further problems. Flint and others have considered geophysically temperate glaciers as most typical of the inland glaciation which covered much of Europe, northern North America and Siberia during the expanded phases of the Pleistocene, whereas others including Ahlmann have suggested that the massive continental glaciers of the Pleistocene were geophysically polar. Thus, the latter advocates consider that present-day Antarctic and Greenland ice sheets represent conditions comparable to those which pertained in the Laurentide and Cordilleran ice sheets. New insights have developed, however, through deep drilling and englacial temperature measurements carried out in a number of different geographical locations in recent years. Such research has shown that each of the geophysical categories can pertain in a glacier system if there is sufficient range of latitude, area and elevation for the requisite climatological factors to pertain.

Because of the foregoing considerations, it is probable that polar, sub-polar, sub-temperate and temperate thermal conditions coexisted in different parts of continental glaciers during the Pleistocene maxima. At times of greatest extension, the ice sheet’s peripheries could have been thermo-physically polar and sub-polar, as on the margins of today’s Greenland icc sheet. But in their most regressive phases, the lower latitude margins were more than likely temperate, with only high interior sectors remaining “cold”. Such combined conditions characterize a fifth thermo-physical category, which in the geophysical sense may be termed polythermal. To some extent all glaciers are poly thermal, except in the final wasting temperate phase when they are fully isothermal.

To elucidate the characteristics of each of these five categories and to identify prototypes with suggested thermal parameters, selected held studies on existing glaciers are discussed and thermal measurements and characteristics illustrated. From the sampled data, arbitrary englacial temperature limits are suggested: for the main body of polar glaciers (—10 to — 70°C); for sub-polar glaciers (—2 to —10°C); for sub-temperate glaciers (-0.1 to —2°C); for temperate glaciers (in summer, 0°C throughout); and for polythermal glaciers (a range across at least two of the foregoing temperature zones). The significance of thermal anomalies, temperature sandwich structures, diagenetic ice zones, and measured shifts in thermodynamic characteristics over a number of years are considered as they aid in the interpretation of ice morphology, glacier regimes, and climatic change.

Type thermo-physical examples are briefly compared from the following areas: the Antarctic and Greenland ice sheets (polar and polythermal), the Nepal Himalaya, Svalbard (polar to sub-polar), Lapland (sub-polar), sub-Arctic Norway (sub-temperate), the Alps (polythermal to temperate), the Canadian Rockies (sub-temperate), the Juneau Icefield, Alaska (sub-temperate to temperate), the Alaskan-British Columbian coast (temperate), glacier systems on Mount Rainier, Washington State (polythermal), and icefields in the St Elias Mountains, Yukon Territory (temperate to polythermal).

The relationship of thermal anomalies is clarified and illustrated within (he defined framework of each category. It is noted how these are manifest by deformation irregularities, differing salinities, and varying heat capacities within the ice. Also discussed is the relationship of changes in thermo-physical characteristics to the sensitivity of ice flow, revealed by changes in entropy and negentropy of glacier systems and by observable shifts from parabolic to rectilinear to surging flow. Finally considered is the long-term implication of secular changes in climate and their influences on englacial thermal regimes which affect the hydrological capacity and fluvial discharge of glaciers as well as their terminal fluctuations. The strong interdependence of all these factors and the total systems analysis which they represent underscore the mandate for a rational thermo-physical classification of glaciers.

A three-dimensional, time-dependent numerical model of ice sheets, developed by Mahaffy (unpublished), has been applied to the general problem of the speed of ice-sheet inception and development over Canada during the last major glaciation. Ice sheet development is assumed to begin due to a lowering of the equilibrium-line altitude with a resulting increase in the accumulation over Baffin Island and Laborador in Canada. This leads to the development of large snow fields over the high plateau areas of this region. Preliminary results are given for the areal extent and the water volume of the ice sheets possible after a period of 10000 years from the initiation of glaciation.

The temperature distribution in a polar glacier is described by the equation of heat conduction,

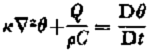1

where K is the thermal diffusivity of ice, Q is the internal heat generation, p is the ice density, and C is the heat capacity. To obtain a solution to this equation, boundary conditions at the surface and bed must be known. The boundary condition at the bed is generally taken to be the temperature gradient in the ice required to conduct the geothermal heat upward into the glacier, with certain modifications where the pressure melting temperature is reached. The boundary condition at the surface is the ice temperature, which is usually assumed to be equal to the mean annual atmospheric temperature. This assumption is incorrect in the ablation area and in the percolation and saturation zones of the accumulation area. In this paper I examine the reasons for the break down of this assumption, and attempt to indicate the magnitude of the error introduced.

The atmospheric temperature at a glacier surface changes seasonally; thus measurements of the “surface” temperature for use with Equation (1) are generally made at some depth, z0, in the glacier below which the effect of these seasonal variations is negligible. If the seasonal variation can be represented by a sinusoidal function, this depth is given by: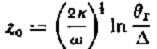2

(Carslaw and Jaeger, 1959, p. 65) where w is the period of the fluctuations (in this case 2π/year), θr is the temperature range from winter minimum to summer maximum, and A is the maximum acceptable change in temperature at depth z0. For example, in the dry zone of the accumulation area if we take K = 16 m2/year, a value appropriate for unpacked snow, θ r = 30 deg, and Δ = 0.4 deg, we obtain z0 = 10 m. This is the basis for the common assumption that the 10 m temperature is approximately equal to the mean annual temperature.

In the superimposed ice zone superimposed ice occurs immediately beneath the winter snow cover, and K for ice at — 10°C is about 38 m2/year. Furthermore, the temperature fluctuation at the ice—snow interface cannot be approximated by a sinusoidal function because the accumulating snow cover insulates the ice during the winter, and because the temperature rises rapidly in the late spring when percolating melt water reaches the interface. Equation (2) can still be used to calculate an approximate value for z0 of about 15 m, but due to the non-sinusoidal temperature variation at the ice-snow interface, the temperature at depth is commonly a few degrees above the mean annual atmospheric temperature.

The magnitude of this difference, which we will call,Δθ can be calculated from Equation (1) if it is assumed that convection, internal heat generation, and transverse and longitudinal conduction are negligible, and if the proper boundary condition at the ice-snow interface is known. The equation to be solved is:

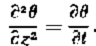3

The boundary condition at depth z0 is taken to be the temperature gradient below this depth. The problem is thus reduced to one of determining the temperature of the ice-snow interface as a function of time,θs(t.

In the soaked zone of the snow cover rests on permeable firn rather than on superimposed ice, and melt water percolating down through the snow pack can penetrate some distance into the firn. Upon refreezing, this water releases the heat of fusion, thus warming the firn. Mathematically, this can be represented by adding an internal heat-production term to Equation (I), thus:

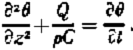4

Due to this internal heat production, Δθ may be substantially larger in the soaked zone than in the superimposed ice zone or ablation area.

In order to determine θs(t) and Q(z), six 30 m bore holes were drilled on the south dome of the Barnes Ice Cap. Five of these holes were along a flow line extending from the divide to the margin. Temperature measurements were made in each hole in mid-July 1973, and three times in June and July 1974. Two finite-difference calculations were carried out with the use of these data. In one, the first of the 1974 measurements was used as an initial condition, and Equation (1) was integrated, using an assumed form of θs(t) as a boundary condition. The form of θS(t) was varied until reasonable agreement was obtained between calculated and measured profiles at the times of the second and third measurements in 1974. This calculation thus permits an estimate of θs(t) during the critical period of melt from early June to mid-July.

In the second calculation, the July 1973 temperature profile was used as an initial condition, and Equation (1) was again integrated, this time simulating a time period of one year. In this model, snow was allowed to accumulate on the ice surface. The accumulation pattern of the snow cover as a function of time was determined from climatic records from nearby weather stations. The temperature variation at the snow-air interface was also determined from these records, using measured lapse rates to correct for differences in altitude (private communication from R. Barry in 1974). Calculations using this model suggest that three factors have a significant influence on the temperature distribution in the ice. One is the fact that most accumulation occurs in the fall and spring, with relatively little accumulation during the winter. The second is that thermal diffusivity of the snow apparently increases during the early spring as atmospheric temperatures begin to rise. The third and most important factor is that the snow-ice interface remains at 0°C late into the fall due to the presence of melt water that percolated down through the accumulating snow cover in the early fall, and the temperature of this interface rises to 0°C early in the spring, again due to percolation of melt water.

The temperature measurements and climatic records were also used to estimate values for Δθ on the Barnes Ice Cap. In the ablation area and superimposed ice zone Δθis 2 to 4 deg. Then there is a rapid increase to about 5 deg in the lower part of the soaked zone. This jump occurs over a distance of only a couple of kilometers across the boundary between the two zones.

Perhaps the most significant consequence of this increase in surface temperature in the superimposed ice and soaked zones is that the temperature throughout this part of a glacier will also increase by approximately the same amount. Thus if the base of a glacier were not already at the pressure melting temperature up-glacier from the soaked zone, it is likely that it would rise to the pressure melting temperature somewhere beneath the soaked or superimposed ice zones. The consequences of this for basal erosion and the entrainment of morainal material need to be examined.

A general two-dimensional numerical model for a typical flow line of a glacier or ice cap has been developed which results in periodical surging for certain ranges of the input parameters. The input includes the bedrock and surface-balance profiles along the flow line, some three-dimensional parameterization depending on the cross-section shape and the flow-line patterns, the flow properties of the ice, and a numerical basal lubrication factor.

The movie shows how a number of different ice masses grow from zero thickness to either steady state or a periodically surging state depending on the input. Typical examples of real surging ice masses from the small to the large are closely matched by the model in many effects such as the period, duration, and speed of the surges, as well as the length and thickness changes.

A preliminary study for the surging potential of a flow line in east Antarctica is also made even though the full temperature modelling is not included. The results indicate that periodic surging of the ice sheet can develop in spite of the expected high viscosity. The resultant surface profile is very similar to the measured profile. For much lower viscosities steady-state, fast-sliding, ice-stream flow develops.

The flat form and high ice velocity of floating glaciers are explained by the absence of shear stresses at the lower surface. In orthogonal co-ordinates with one axis normal to the upper and lower surfaces shear stresses in these glaciers are absent. Another important peculiarity of ice shelves is their essential non-isothermality. Among them two dynamically different types are distinguished, which are described by different models.

A. External ice shelves join the coast at one edge and at some distance from it can expand freely in all directions. They can be considered with sufficient accuracy as flat plates without any physical differences between the directions of the horizontal plane, except that strains lead to the movement relative to the fixed edge. Thus the problem of thermodynamics becomes one-dimensional. In the affine dimensionless system of co-ordinates, the equations of the dynamics are simplified and together with the rheological equation lead to the non-linear integro-differential equation involving the reduced temperature. For the quasi-steady case, the boundary problem for this equation is solved by means of the method of sewing together of asymptotic expansions. It is shown that the stability of the thermodynamic regime in external ice shelves takes place only when the stream lines pass through both glacier surfaces, because in this case the advection removes the dissipative heat. In the case of ice coming from the upper and lower surfaces in opposite directions, the regime is unsteady because of the internal accumulation of heat.

B. Internal ice shelves are limited by coasts from various sides and interact with them dynamically. In the boundary zone coasts provide a braking action and outside it they prevent sideways spreading. The relation between horizontal stresses is conditioned by the configuration of coasts, therefore the angle between the coasts, or between the directions of ice flow from them, is included essentially into the equations of thermodynamics. Another complication is connected with the considerable change of the temperature and of the accumulation- ablation rate at the upper and lower surfaces of the glacier along flow lines. Integro-differential equation for the temperature in this case is more complicated, but its solution is analogous to the case above. In the coastal zone the thermodynamics are described by other equations in connection with the predominance of the shear stress in the plane parallel to the coast.

During the 1973-74 Antarctic field season, two electrical resistivity profiles were completed along directions perpendicular to each other at a site in the south-easternpart of the Ross Ice Shelf. These profiles differ from each other only at short electrode spacings (less than 10 m) indicating no measurable horizontal anisotropy below the uppermost firn zone. The shape of the apparent resistivity curves is similar to that found by Hochstein on the Ross Ice Shelf near Roosevelt Island, but is displaced toward lower resistivities despite the colder 10 m temperature (—29°C instead of —26°C) at the more southerly site. Some factor other than temperature must therefore be effective in determining the overall magnitude of the resistivities in the shelf, although the variation with depth can still be expected to be primarily a temperature phenomenon.

A computer program has been written to calculate apparent resistivities based on Crary’s analysis of temperatures in an ice shelf. Results are not yet available; when completed they should indicate the sensitivity of the resistivity measurements to differences in the temperature- depth profile, and hence their usefulness in estimating bottom melt/freeze rates.

In the case of a non-isothermal glacier it is necessary to integrate the equations of dynamics together with the equation of heat conduction, heat transfer, and heat generation because of the interdependence (1) of strain-rate of ice on its temperature, and (2) of ice temperature on the rate of heat transfer by moving ice and on the intensity of heat generation in its strain. In view of the complexity of the whole system of equations, simplified mathematical models have been constructed for dynamically different glaciers. The present model concerns land glaciers with thicknesses much less than their horizontal dimensions and radii of curvature of large bottom irregularities, so that the method of a thin boundary layer may be used. The principal assumption is the validity of averaging over a distance of the order of magnitude of ice thickness.

Two component shear stresses parallel to the bottom in glaciers of this type considerably exceed the normal stresses and the third shear stress, so the dynamics are described by a statically determined system of equations. For the general case, expressions for the stresses have been obtained in dimensionless affine orthogonal curvilinear coordinates, parallel and normal to the glacier bottom, and taking into account the geometry of the lower and upper surfaces. The statically undetermined problem for ice divides is solved using the equations of continuity and rheology, so the result for stresses depends considerably on temperature distribution. In the case of a flat bottom the dynamics of an ice divide is determined by the curvature of the upper surface.

The calculation of the interrelating velocity and temperature distributions is made by means of the iteration of solutions (1) for the components of velocity from the stress expressions using the rheological equations (a power law or the more precise hyberbolic one) with the assigned temperature distribution, and (2) for the temperature with the assigned velocity distribution. The temperature distribution in the coordinate system used is determined by a parabolic equation with a small parameter at the principal derivative. Its solution is reduced to the solution of a system of recurrent non-uniform differential equations of the first order by means of a series expansion of the small parameter: the right part for the largest term of the expansion contains a function of the heat sources, and for the other terms it contains the second derivative along the vertical coordinate from the previous expansion term.

Thus advection makes the main contribution to the heat transfer, and temperature in a glacier is distributed along the particle paths, changing simultaneously under the influence of heat generation. A relatively thin conducting boundary layer adjoins the upper and lower surfaces of a glacier, playing the role of a temperature damper in the ablation area. The equation of heat conduction (at the free surface) or of heat conduction and heat transfer (at the bottom) with the boundary conditions, and with the condition of the connection with the solution of the problem for the internal temperature distribution, is being solved for the boundary layer because of its small thickness. Beyond the limits of the boundary layer, heat conduction makes a small change in the temperature distribution, which can be calculated with any degree of accuracy.

In sub-isothermal glaciers heat conduction plays the main role in the formation of the temperature field, and the contribution of advection is relatively small. The dependence of the strain-rate on the temperature is simplified by a linear approximation. If the whole range of the temperature change in a glacier does not exceed ≈ 3 deg, with the power rheological law the quasi-steady temperature distribution is described by a simple analytical dependence. In the upper part of the ice, the temperature varies with depth almost linearly; the deflection from the linear distribution is essentially in the lower part.

Recent measurements of the water level (pressure head) in drill holes and natural moulins on two glacier tongues in Switzerland (Oberaletschgletscher and Gornergletscher) have confirmed that in those holes which link up to a well developed subglacial drainage system the daily piezometric fluctuations are in the order of 100 m (10 bar) and more. From the fact that it is relatively easy to establish such links (in our experiments at ice depths between 150 and 300 m), it is implied that an extended network of subglacial channels and cavities will be subjected to equally large pressure fluctuations with a mean water pressure considerably below the mean ice pressure at the bed. The scope of the present paper is to discuss some of the thermal effects of the low water pressure and its fluctuations.

The effect in the ice—assuming temperate ice with a certain water content—is a positive temperature anomaly around the channel, in accordance with the stress field. The radial temperature profile in the ice around a conduit with a circular cross-section follow's directly from the solution for the stress field, and the heat flux can be deduced, allowing for the ice flow towards the conduit. Pressure changes in the conduit cause a rapid change of temperature (with an associated change in water content) and a related change in heat and ice flow. In the case of a channel or cavity at the glacier bed, the temperature fluctuation produced in the channel and the surrounding ice propagates into the substratum. With rising water pressure, i.e. falling temperature, the substratum becomes a heat source and some melting will occur at the ice/rock interface in a fringe zone around channels and cavities. It is this process which may help to explain the increased sliding component of glacier motion at the time of high melt-water run-off.

Another intriguing question is what happens in a highly permeable substratum (shattered rock, moraine) at some distance away from a channel. The temperature profile is determined by the pressure melting point within the glacier down to the bed, and the positive geothermal gradient with increasing depth in the substratum below. The water pressure in the substratum is approximately equal to that in the channel, that is to say well below the mean pressure at the glacier bed. There is therefore an uppermost layer of the substratum at a temperature below the freezing temperature of the interstitial water, implying that the water must be frozen in this layer. This is one way to look at the problem. Starting out from the impermeable frozen layer it may be argued that the water film at the glacier bed is at a high pressure and the interstitial ice should melt until the water breaks through at the lower freezing boundary. This could only happen where and as long as there is no appreciable drainage of the water film and interstitial water. As soon as the water breaks through, the pressure will drop and presumably just enough leakage will be sustained to lead to a pressure drop across the frozen layer in accordance with the temperature profile. A generally impermeable glacier bed results as a most likely model, with permeable bands along subglacial drainage channels and eventual leakage holes in between. Taking the pressure fluctuations into account, one finds that temperature fluctuations have to be expected originating at the lower boundary of the frozen substratum, involving frost cycles. The erosive effectiveness of these will however be limited to the equivalent of the pressure cycles. (A double pressure amplitude of 130 m of water head corresponds roughly to a double temperature amplitude of 0.1 deg.)

In terms of the theory of oscillations, rapid glacier advances (glacier surges) are relaxation self-oscillation, and large glacier advances of the same character dependent on climate are the result of interaction between forced and self-exciting oscillations.

The relation is found between average shear stress and sliding velocity of pure and of moraine-containing ice along the bottom, taking into account the real thermal and kinematic boundary conditions, the different dependence of the ice melting point on hydrostatic pressure

and on normal component of the stress deviator, and dry friction against the bottom. In the regime of bottom melting, a communicating system of subglacial drainage channels is formed along (he borders of distal slopes of bottom irregularities. Variations of effective roughness lead to the forced variations of sliding velocity depending on the surface melting rate.

Relaxation self-oscillations of glaciers are caused by the alternation of “sticking” to the bottom in the phase of restoration and of rapid sliding along the bottom in the phase of relaxation because of the changes in the concentration of moraine material in the bottom layer of ice and of the force of dry friction against the bottom of a glacier.