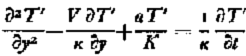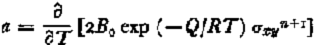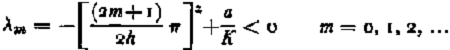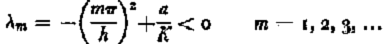We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 02 May 2017
The equation governing the growth or decay of a temperature perturbation T’ in an ice slab under shear stress σxy is
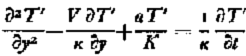
where K and k are respectively the thermal conductivity and diffusivity of ice, KB-v is the advection velocity normal to the bed and
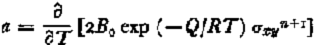
is the rate of increase of strain heating with temperature assuming a power law for flow. For a slab of infinite thickness under constant stress and at constant ambient temperature, T Fourier analysis gives -k2+a/k < o as the condition for stability where k is the wave number of a sinusoidal perturbation. When the slab has finite thickness the stability depends on the sign of the eigenvalues λm of the perturbation equation and on the boundary condition at the ice-rock interface. In general the eigenfunctions and eigenvalues must be found by approximate methods such as the Rayleigh-Ritz procedure but in the case where the stress and ambient temperature are constant over the slab thickness and there is no advection the eigenfunctions are either sines or cosines depending on the boundary conditions.
In this special case the stability condition is
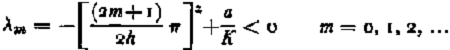
if the bed is frozen and
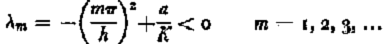
if it is at the melting point. The eigenvalue associated with the smallest value of m is the least stable so the maximum stable thickness is thus h = ½ π(a/K)1/2 if the bed is frozen or h = π (a/K)1/2 if it is at the melting point. For typical flow-law parameters these depths are around 250 m and 500 m respectively. The eigenvalues are related in a simple way to the growth or decay rates of the eigenfunctions: (K λm)–1 is the time constant for the mth eigenfunction.
Depth-dependent stress, temperature, and advection have a marked effect on stability. A slab in which stress and temperature increase to values B and TB at the bed is considerably more stable than a slab held at constant stressσB and a constant temperature TB. Advection normal to the bed also has a major influence on stability. If the advection velocity is taken to vary linearly with depth and the bed is frozen, the effect of upward advection is to decrease stability and of downward advection to increase it. When the bed is temperate the effect of advection is more complex: downward advection increases stability but upward advection may increase or decrease it depending on the magnitude of the advection velocity.
W. F. Budd: Have you examined real situation values in your analysis to see the limits for which you can obtain stable solutions?
G. K. C. Clarke: I have just begun to do this and would like to satisfy myself that the numerical methods used to compute eigenvalues are sound and to test a range of flow laws before making generalizations about the region of stability.
You have
Access
