We theoretically analyse the impact of subsurface currents induced by internal waves on nonlinear Stokes surface waves. We present analytical and numerical solutions of the modulation equations under conditions that are close to group velocity resonance. Our results show that smoothing of the downcurrent surface waves is accompanied by a relatively high-frequency modulation, while the profile of the opposing current is reproduced by the surface wave's envelope. We confirm the possibility of generating an internal wave forerunner that is a modulated surface wave packet. Long surface waves can create such a wave modulation forerunner ahead of the internal wave, while other relatively short surface waves comprise the trace of the internal wave itself. Modulation of surface waves by a periodic internal wavetrain may exhibit a characteristic period that is less than the internal wave period. This period can be non-uniform while the wave crosses the current zone. Our results confirm that surface wave excitation by means of internal waves, as observed at their group resonance frequencies, is efficient only in the context of opposing currents.

This paper deals with the definition and description of optimal streaky (S) perturbations in a Blasius boundary layer. First, the asymptotic behaviours of S-perturbations near the free stream and the leading edge are studied to conclude that the former is slaved to the solution inside the boundary layer. Based on these results, a quite precise numerical scheme is constructed that allows concluding that S-perturbations produced inside the boundary layer, near the leading edge, can be defined in terms of just one streamwise-evolving solution of the linearized equations, associated with the first eigenmode of an eigenvalue problem first formulated by Luchini (J. Fluid Mech., vol. 327, 1996, p. 101). Such solution may be seen as an internal unstable streaky mode of the boundary layer, similar to eigenmodes of linearized stability problems. The remaining modes decay streamwise. Thus, the definition of streaks in terms of an optimization problem that is used nowadays is not necessary.

Source-driven ocean currents that flow over topographic sills are important initiation sites for the abyssal component of the thermohaline circulation. These overflows exhibit vigorous space and time variability over many scales as they progress from a predominately gravity-driven downslope flow to a geostrophic along-slope current. Observations show that in the immediate vicinity of a sill, grounded abyssal ocean overflows can possess current speeds greater than the local long internal gravity wave speed with bottom friction and downslope gravitational acceleration dominating the flow evolution. It is shown that these dynamics lead to the mixed frictionally induced and Kelvin–Helmholtz instability of grounded abyssal overflows. Within the overflow, the linearized instabilities correspond to bottom-intensified baroclinic roll waves, and in the overlying water column amplifying internal gravity waves are generated. The stability characteristics are described as functions of the bottom drag coefficient and slope, Froude, bulk Richardson and Reynolds numbers associated with the overflow and the fractional thickness of the abyssal current compared to the mean depth of the overlying water column. The marginal stability boundary and the boundary separating the parameter regimes in which the most unstable mode has a finite or infinite wavenumber are determined. When it exists, the high-wavenumber cutoff is obtained. Conditions for the possible development of an ultraviolet catastrophe are determined. In the infinite-Reynolds-number limit, an exact solution is obtained which fully includes the effects of mean depth variations in the overlying water column associated with a sloping bottom. For parameter values characteristic of the Denmark Strait overflow, the most unstable mode has a wavelength of about 19 km, a geostationary period of about 14 hours, an e-folding amplification time of about 2 hours and a downslope phase speed of about 74 cm s−1.

Velocity, mixture fraction and temperature spectra obtained from five direct numerical simulations of non-reacting and reacting shear layers, using the infinitely fast chemistry approximation, are analysed. Two different global chemical reactions corresponding to methane and hydrogen combustion with air, respectively, are considered. The effect of heat release, i.e. density variation, on the inertial and dissipation turbulence subrange of the spectra is investigated. Analysis of the database supports the experimentally available measurements of spectra in turbulent reacting flows showing that heat release effects can be scaled out by utilizing Favre-averaged (density-weighted) large-scale turbulence quantities. This is supported by the simulation results for velocity and mixture fraction in our moderate-Reynolds-number flows but it appears to be less supported in the dissipation subrange of the temperature spectra. The departure from universal scaling using Favre-averaged quantities in the temperature spectrum, which is evident in the dissipation subrange, appears to be caused by the strong nonlinearity of the state relationship relating the mixture fraction to the temperature, as has been suggested previously. These effects are less pronounced at intermediate wavenumbers. Analysis suggests that the nonlinear state relationship and the spectra of mixture fraction moments can be used to reconstruct the temperature spectrum across the flow. Moreover, the governing equation for the temperature variance is analysed to identify a possible surrogate for the overall rate of dissipation of temperature fluctuations and their corresponding dissipation length scale. This scaling analysis is then used to separate planes across the shear layer where the temperature dissipation length scale is alike that of the mixture fraction from regions where smaller length scales are present, and are evidenced in the dissipation subrange using Kolmogorov scaling. In our simulations, these regions correspond to the centre of the shear layer and the mean flame location. The new estimate for the temperature dissipation length scale is able to collapse the compensated spectra profiles at all planes across the shear layer for all simulations.

Studies of vortical interactions in boundary layers have often invoked the continuous spectrum of the Orr–Sommerfeld (O-S) equation. These vortical eigenmodes provide a link between free-stream disturbances and the boundary-layer shear – a link which is absent in the inviscid limit due to shear sheltering. In the presence of viscosity, however, a shift in the dominant balance in the operator determines the structure of these eigenfunctions inside the mean shear. In order to explain the mechanics of shear sheltering and the structure of the continuous modes, both numerical and asymptotic solutions of the linear perturbation equation are presented in single- and two-fluid boundary layers. The asymptotic analysis identifies three limits: a convective shear-sheltering regime, a convective–diffusive regime and a diffusive regime. In the shear-dominated limit, the vorticity eigenfunction possesses a three-layer structure, the topmost being a region of exponential decay. The role of viscosity is most pronounced in the diffusive regime, where the boundary layer becomes ‘transparent’ to the oscillatory eigenfunctions. Finally, the convective–diffusive regime demonstrates the interplay between the the accumulative effect of the shear and the role of viscosity. The analyses are complemented by a physical interpretation of shear-sheltering mechanism. The influence of a wallfilm, in particular viscosity and density stratification, and surface tension are also evaluated. It is shown that a modified wavenumber emerges across the interface and influences the penetration of vortical disturbances into the two-fluid shear flow.

Traditional a posteriori tests of subgrid-scale (SGS) models often compare large eddy simulation (LES) profiles of various statistics with measurements. In this study we propose and employ a new a posteriori test to study SGS model performance. We compare the conditional means of the LES-generated SGS stress and stress production rate conditional on the resolvable-scale velocity with measurements. These statistics must be reproduced by the SGS model for LES to correctly predict the one-point resolvable-scale velocity joint probability density function. Our tests using data obtained in convective atmospheric boundary layers show that the a posteriori results are consistent with our a priori tests based on the same conditional statistics. The strengths and deficiencies of the models observed here were also identified in our a priori tests. The remarkable consistency between the two types of tests suggests that statistical model tests based on the conditional SGS stress and its production rate are a highly capable approach for identifying specific model deficiencies and for evaluating SGS model performance in simulations.

Heterogeneous condensation of vapours mixed with a carrier gas in the stagnation point boundary layer flow near a cold wall is considered in the presence of solid particles much larger than the mean free path of vapour particles. The supersaturated vapour condenses on the particles by diffusion, and particles and droplets are thermophoretically attracted to the wall. Assuming that the heat of vaporization is much larger than kB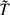∞, where 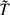∞ is the temperature far from the wall, vapour condensation occurs in a condensation layer (CL). The CL width and characteristics depend on the parameters of the problem, and a parameter R yielding the rate of vapour scavenging by solid particles is particularly important. Assuming that the CL is so narrow that temperature, particle density and velocity do not change appreciably inside it, an asymptotic theory is found, the δ-CL theory, that approximates very well the vapour and droplet profiles, the dew point shift and the deposition rates at the wall for wide ranges of the wall temperature 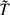w and the scavenging parameter R. This theory breaks down for 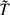w very close to the maximum temperature yielding non-zero droplet deposition rate, 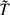w, M. If the width of the CL is assumed to be zero (0-CL theory), the vapour density reaches local equilibrium with the condensate immediately after it enters the dew surface. The 0-CL theory yields appropriate profiles and deposition rates in the limit as R → ∞ and also for any R, provided 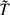w is very close to 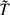w, M. Nonlinear multiple scales also improve the 0-CL theory, providing good uniform approximations to the deposition rates and the profiles for large R or for moderate R and 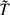w very close to 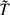w, M, but it breaks down for other values of 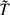w and small R.

We present the results of a combined theoretical and numerical investigation of the rim-driven retraction of flat fluid sheets in both planar and circular geometries. Particular attention is given to the influence of the fluid viscosity on the evolution of the sheet and its bounding rim. In both geometries, after a transient that depends on the sheet viscosity and geometry, the film edge eventually attains the Taylor–Culick speed predicted on the basis of inviscid theory. The emergence of this result in the viscous limit is rationalized by consideration of both momentum and energy arguments. We first consider the planar geometry considered by Brenner & Gueyffier (Phys. Fluids, vol. 11, 1999, p. 737) and deduce new analytical expressions for the speed of the film edge at the onset of rupture and the evolution of the maximum film thickness for viscous films. In order to consider the expansion of a circular hole, we develop an appropriate lubrication model that predicts the form of the early stage dynamics of film rupture. Simulations of a broad range of flow parameters confirm the importance of geometry on the dynamics, verifying the exponential hole growth reported in early experimental studies. We demonstrate the sensitivity of the initial retraction speed on the film profile, and so suggest that the anomalous rate of retraction reported in these experiments may be attributed in part to geometric details of the puncture process.

Evolution of flat-plate wakes in sink flow has been studied both analytically and experimentally. For such wakes, a similarity solution is derived which considers simultaneous presence of both laminar and turbulent stresses inside the wake. This solution utilizes an additional Reynolds-stress term which represents the fluctuations similar to those in wall-bounded flows, accounting for the fluctuations originating from the plate boundary layer. In this solution, it is shown that the total stress, the sum of laminar and Reynolds shear stresses, becomes self-similar. To investigate the accuracy of the analytical results, the wake of a flat plate located at the centreline of a planar contraction is studied using hot-wire anemometry. Wakes of both tapered and blunt edges are considered. The length of the plates and the flow acceleration number K = 6.25 × 10−6 are chosen such that the boundary-layer profiles at the plate edge approach the self-similar laminar solution of Pohlhausen (Z. Angew. Math. Mech., vol. 1, 1921, p. 252). A short plate in which the boundary layer at the edge does not fully relaminarize is also considered. The development of the turbulent diffusivity used in the analysis is determined empirically for each experimental case. We have shown that the obtained similarity solutions, accounting also for the initial conditions in each case, generally agree well with the experimental results even in the near field. The results also show that the mean velocity of the transitional wake behind a tapered edge becomes self-similar almost immediately downstream of the edge.

In this work the thermocapillary-induced motion of partially engulfed compound drops is considered. This phenomenon occurs in many natural and technological processes in which heat is exchanged between such hybrid drops and the medium around them through the interfaces. Two types of thermal fields and the resulting motions are studied; flow induced by an external temperature gradient and spontaneous thermocapillary motion. For the first flow type, it was found that, in general, the motion is induced in the direction of the temperature gradient. However, under certain physical conditions and drops' configuration a motion against the temperature gradient may be observed. In the second case, spontaneous thermocapillary motion, the compound drop moves due to surface tension gradients which result from the geometric non-uniformity of the system. Results are presented for several parameters such as configuration of the compound drop, viscosity, thermal conductivity ratio, the dependence of the various interfacial tensions on temperature and the volume ratio of the phases within the drop.

New solutions of the Navier–Stokes equations are presented for axisymmetric vortex flows subject to strain and to suction or injection. Those expressible in simple separable or similarity form are emphasized. These exhibit the competing roles of diffusion, advection and vortex stretching.

We present the first solution to a boundary motion planning problem for the Navier–Stokes equations, linearized around the parabolic equilibrium in a three-dimensional channel flow. The pressure and skin friction at one wall are chosen as the reference outputs as they are the most readily measurable ‘wall-restricted’ quantities in experimental fluid dynamics and also because they play a special role as performance metrics in aerodynamics. The reference velocity input is applied at the opposite wall. We find the exact (method independent) solution to the motion planning problem using the PDE (partial differential equation) backstepping theory. The motion planning solution results in open-loop controls, which produce the reference output trajectories only under special initial conditions for the flow velocity field. To achieve convergence to the reference trajectory from other (nearby) initial conditions, we design a feedback controller. We also present a detailed examination of the closed-form solutions for gains and the behaviour of the motion planning solution as the wavenumbers grow or the Reynolds number grows. Numerical results are shown for the motion planning problem.

The passive scalar field of a temporally evolving shear layer is investigated using gradient trajectories as a means to analyse the scalar probability density function and the conditional scalar dissipation rate in the presence of external intermittency. These results are of significance for turbulent combustion, where improved predictions of the statistics of the conditional dissipation rate are needed in several models. First, the variation of the conventional first and second moments of the conditional dissipation rate across the layer is quantitatively documented in detail. A strong dependence of the conditional dissipation rate on the lateral position and on the conditioning value of the scalar is observed. The dependence on the transverse distance to the centre-plane partially explains the double-hump profile usually reported when this dependence is ignored. The variation with the scalar observed in the ratio between the second and first moments would invalidate certain assumptions commonly done in turbulent combustion. It is also seen that conditioning on the scalar does not reduce the fluctuation of the dissipation rate with respect to unconditional values. Next, the role of external intermittency in these results is investigated. For that purpose, the flow is partitioned into different zones based on different types of gradient trajectories passing through each point, thereby introducing non-local information in comparison with the standard turbulent/non-turbulent separation based on the conventional intermittency function. In addition to the homogeneous outer regions, three zones are identified: a turbulent zone, a turbulence interface and quasi-laminar diffusion layers. The relative contribution from each of these zones to the conventional intermittency factor is reported. The statistics are then conditioned on each of these zones, and the spatial variation of the scalar distribution and of the conditional scalar dissipation rate is explained in terms of the observed zonal statistics. For the Reynolds numbers of the present simulation, between 1500 and 3000 based on the vorticity thickness and the velocity difference, and a Schmidt number equal to 1, it results that the major contribution to both statistics is due to the turbulence interfaces. At the same time, the turbulent zone shows a distinct behaviour, being approximately homogeneous but anisotropic.

The effect of an electric field on a periodic array of two-dimensional liquid drops suspended in simple shear flow is studied numerically. The shear is produced by moving the parallel walls of the channel containing the fluids at equal speeds but in opposite directions and an electric field is generated by imposing a constant voltage difference across the channel walls. The level set method is adapted to electrohydrodynamics problems that include a background flow in order to compute the effects of permittivity and conductivity differences between the two phases on the dynamics and drop configurations. The electric field introduces additional interfacial stresses at the drop interface and we perform extensive computations to assess the combined effects of electric fields, surface tension and inertia. Our computations for perfect dielectric systems indicate that the electric field increases the drop deformation to generate elongated drops at steady state, and at the same time alters the drop orientation by increasing alignment with the vertical, which is the direction of the underlying electric field. These phenomena are observed for a range of values of Reynolds and capillary numbers. Computations using the leaky dielectric model also indicate that for certain combinations of electric properties the drop can undergo enhanced alignment with the vertical or the horizontal, as compared to perfect dielectric systems. For cases of enhanced elongation and alignment with the vertical, the flow positions the droplets closer to the channel walls where they cause larger wall shear stresses. We also establish that a sufficiently strong electric field can be used to destabilize the flow in the sense that steady-state droplets that can exist in its absence for a set of physical parameters, become increasingly and indefinitely elongated until additional mechanisms can lead to rupture. It is suggested that electric fields can be used to enhance such phenomena.

To reduce the costs of construction, operation, maintenance, energy storage and grid connection, some devices for extracting energy from sea waves are likely to be installed on the coast. We study theoretically a single oscillating water column (OWC) installed at the tip of a long and thin breakwater. The linearized problems of radiation and scattering for a hollow cylinder with an open bottom are then solved by the usual method of eigenfunction expansions and integral equations. Since a thin breakwater is the limit of a wedge, an exact solution for the diffraction by a solid cylinder at the tip of a wedge is derived to facilitate the analysis. Following Sarmento & Falcão (J. Fluid Mech., vol. 150, 1985, pp. 467–485), power takeoff by Wells turbines is modelled by including air compressibility in the chamber above the water surface. The effects of air compressibility on the extraction efficiency is studied. It is shown that for this simple geometry the angle of incidence affects the waves outside the structure but not the extracted power.

The nonlinear stability of two-phase core-annular flow in a cylindrical pipe is studied. A constant pressure gradient drives the flow of two immiscible liquids of different viscosities and equal densities, and surface tension acts at the interface separating the phases. Insoluble surfactants are included, and we assess their effect on the flow stability and ensuing spatio-temporal dynamics. We achieve this by developing an asymptotic analysis in the limit of a thin annular layer – which is usually the relevant regime in applications – to derive a coupled system of nonlinear evolution equations that govern the dynamics of the interface and the local surfactant concentration on it. In the absence of surfactants the system reduces to the Kuramoto–Sivashinsky (KS) equation, and its modifications due to viscosity stratification (present when the phases have unequal viscosities) are derived elsewhere. We report on extensive numerical experiments to evaluate the effect of surfactants on KS dynamics (including chaotic states, for example), in both the absence and the presence of viscosity stratification. We find that chaos is suppressed in the absence of viscosity differences and that the new flow consists of successive windows (in parameter space) of steady-state travelling waves separated by time-periodic attractors. The intricate structure of the travelling pulses is also explained physically. When viscosity stratification is present we observe a transition from time-periodic dynamics, for instance, to steady-state travelling wave pulses of increasing amplitudes and speeds. Numerical evidence is presented that indicates that the transition occurs through a reverse Feigenbaum cascade in phase space.

An experimental and numerical systematic study of the growth of the Richtmyer–Meshkov instability-induced mixing following a re-shock is made, where the initial shock moves from the light fluid to the heavy one, over an incident Mach number range of 1.15–1.45. The evolution of the mixing zone following the re-shock is found to be independent of its amplitude at the time of the re-shock and to depend directly on the strength of the re-shock. A linear growth of the mixing zone with time following the passage of the re-shock and before the arrival of the reflected rarefaction wave is found. Moreover, when the mixing zone width is plotted as a function of the distance travelled, the growth slope is found to be independent of the re-shock strength. A comparison of the experimental results with direct numerical simulation calculations reveals that the linear growth rate of the mixing zone is the result of a bubble competition process.