We computationally investigate the unsteady pulsatile propagation of a finger of air through a liquid-filled cylindrical rigid tube. The flow field is governed by the unsteady capillary number CaQ(t)=μQ*(t*)/πR2γ, where R is the tube radius, Q* is the dimensional flow rate, t* is the dimensional time, μ is the viscosity, and γ is the surface tension. Pulsatility is imposed by CaQ(t) consisting of both mean (CaM) and oscillatory (CaΩ components such that CaQ(t)=CaM+CaΩ sin(Ωt). Dimensionless frequency and amplitude parameters are defined, respectively, as Ω=μωR/γ and A=2CaΩ/Ω, with Ω epresenting the frequency of oscillation. The system is accurately described by steady-state behaviour if CaΩ<CaM; however, when CaΩ>CaM, reverse flow exists during a portion of the cycle, leading to an unsteady regime. In this unsteady regime, converging and diverging surface stagnation points translate dynamically along the interface throughout the cycle and may temporarily separate to create internal stagnation points at high Ω. For CaΩ<10CaM, the bubble tip pressure drop ΔPtip may be estimated accurately from the pressure measured downstream of the bubble tip when corrections for the downstream viscous component of the pressure drop are applied. The normal stress gradient at the tube wall ∂τn/∂z is examined in detail, because this has been shown to be the primary factor responsible for mechanical damage to epithelial cells during pulmonary airway reopening (Bilek, Dee & Gaver III 2003; Kay et al. 2004). In the unsteady regime, local film-thinning produces high ∂τn/∂z at low CaΩ; however, film thickening at moderate Ca protects the tube wall from large ∂τn/∂z. This stress field is highly dynamic and exhibits intriguing spatial and temporal characteristics that may be used to reduce ventilator-induced lung injury.

Motivated by the propulsion mechanisms adopted by gastropods, annelids and other invertebrates, we consider shape optimization of a flexible sheet that moves by propagating deformation waves along its body. The self-propelled sheet is separated from a rigid substrate by a thin layer of viscous Newtonian fluid. We use a lubrication approximation to model the dynamics and derive the relevant Euler–Lagrange equations to simultaneously optimize swimming speed, efficiency and fluid loss. We find that as the parameters controlling these quantities approach critical values, the optimal solutions become singular in a self-similar fashion and sometimes leave the realm of validity of the lubrication model. We explore these singular limits by computing higher-order corrections to the zeroth order theory and find that wave profiles that develop cusp-like singularities are appropriately penalized, yielding non-singular optimal solutions. These corrections are themselves validated by comparison with finite element solutions of the full Stokes equations, and, to the extent possible, using recent rigorous a priori error bounds.

The deformation of a Newtonian/viscoelastic drop suspended in a viscoelastic fluid is investigated using a three-dimensional front-tracking finite-difference method. The viscoelasticity is modelled using the Oldroyd-B constitutive equation. Matrix viscoelasticity affects the drop deformation and the inclination angle with the flow direction. Numerical predictions of these quantities are compared with previous experimental measurements using Boger fluids. The elastic and viscous stresses at the interface, polymer orientation, and the elastic and viscous forces in the domain are carefully investigated as they affect the drop response. Significant change in the drop inclination with increasing viscoelasticity is observed; this is explained in terms of the first normal stress difference. A non-monotonic change – a decrease followed by an increase – in the steady-state drop deformation is observed with increasing Deborah number (De) and explained in terms of the competition between increased localized polymer stretching at the drop tips and the decreased viscous stretching due to change in drop orientation angle. The transient drop orientation angle is found to evolve on the polymer relaxation time scale for high De. The breakup of a viscous drop in a viscoelastic matrix is inhibited for small De, and promoted at higher De. Polymeric to total viscosity ratio β was seen to affect the result through the combined parameter βDe indicating a dominant role of the first normal stress difference. A viscoelastic drop in a viscoelastic matrix with matched relaxation time experiences less deformation compared to the case when one of the phases is viscous; but the inclination angle assumes an intermediate value between two extreme cases. Increased drop phase viscoelasticity compared to matrix phase leads to decreased deformation.

The linear stability of inviscid non-diffusive density-stratified shear flow in a rotating frame is considered. A temporally periodic base flow, characterized by vertical shear S, buoyancy frequency N and rotation frequency f, is perturbed by infinitesimal inertia–gravity waves. The temporal evolution and stability characteristics of the disturbances are analysed using Floquet theory and the growth rates of unstable solutions are computed numerically. The global structure of solutions is addressed in the dimensionless parameter space (N/f, S/f, φ) where φ is the wavenumber inclination angle from the horizontal for the wave-like perturbations. Both weakly stratified rapidly rotating flows (N<f) and strongly stratified slowly rotating flows (N>f) are examined. Distinct families of unstable modes are found, each of which can be associated with nearby stable solutions of periodicity T or 2T where T is the inertial frequency 2π/f. Rotation is found to be a destabilizing factor in the sense that stable non-rotating shear flows with N2/S2>1/4 can be unstable in a rotating frame. Morever, instabilities by parametric resonance are found associated with free oscillations at half and integer multiples of the inertial frequency.

We consider the kinematic dynamo problem for a velocity field consisting of a mixture of turbulence and coherent structures. For these flows the dynamo growth rate is determined by a competition between the large flow structures that have large magnetic Reynolds number but long turnover times and the small ones that have low magnetic Reynolds number but short turnover times. We introduce the concept of a quick dynamo as one that reaches its maximum growth rate in some (small) neighbourhood of its critical magnetic Reynolds number. We argue that if the coherent structures are quick dynamos, the overall dynamo growth rate can be predicted by looking at those flow structures that have spatial and temporal scales such that their magnetic Reynolds number is just above critical. We test this idea numerically by studying 2.5-dimensional dynamo action which allows extreme parameter values to be considered. The required velocities, consisting of a mixture of turbulence with a given spectrum and long-lived vortices (coherent structures), are obtained by solving the active scalar equations. By using spectral filtering we demonstrate that the scales responsible for dynamo action are consistent with those predicted by the theory.

We examine the buoyancy-driven rise of a bubble in a Newtonian or a viscoplastic fluid assuming axial symmetry and steady flow. Bubble pressure and rise velocity are determined, respectively, by requiring that its volume remains constant and its centre of mass remains fixed at the centre of the coordinate system. The continuous constitutive model suggested by Papanastasiou is used to describe the viscoplastic behaviour of the material. The flow equations are solved numerically using the mixed finite-element/Galerkin method. The nodal points of the computational mesh are determined by solving a set of elliptic differential equations to follow the often large deformations of the bubble surface. The accuracy of solutions is ascertained by mesh refinement and predictions are in very good agreement with previous experimental and theoretical results for Newtonian fluids. We determine the bubble shape and velocity and the shape of the yield surfaces for a wide range of material properties, expressed in terms of the Bingham Bn= Bond Bo = and Archimedes Ar= numbers, where ρ* is the density, μ*o the viscosity, γ* the surface tension and τ*y the yield stress of the material, g* the gravitational acceleration and R*b the radius of a spherical bubble of the same volume. If the fluid is viscoplastic, the material will not be deforming outside a finite region around the bubble and, under certain conditions, it will not be deforming either behind it or around its equatorial plane in contact with the bubble. As Bn increases, the yield surfaces at the bubble equatorial plane and away from the bubble merge and the bubble becomes entrapped. When Bo is small and the bubble cannot deform from the spherical shape the critical Bn is 0.143, i.e. it is a factor of 3/2 higher than the critical Bn for the entrapment of a solid sphere in a Bingham fluid, in direct correspondence with the 3/2 higher terminal velocity of a bubble over that of a sphere under the same buoyancy force in Stokes flow. As Bo increases allowing the bubble to squeeze through the material more easily, the critical Bingham number increases as well, but eventually it reaches an asymptotic value. Ar affects the critical Bn value much less.

Two-dimensional direct numerical simulation (DNS) of receptivity to acoustic disturbances radiating onto a flat plate with a sharp leading edge in the Mach 6 free stream is carried out. Numerical data obtained for fast and slow acoustic waves of zero angle of incidence are consistent with the asymptotic theory. Numerical experiments with acoustic waves of non-zero angles of incidence reveal new features of the disturbance field near the plate leading edge. The shock wave, which is formed near the leading edge owing to viscous–inviscid interaction, produces a profound effect on the acoustic near field and excitation of boundary-layer modes. DNS of the porous coating effect on stability and receptivity of the hypersonic boundary layer is carried out. A porous coating of regular porosity (equally spaced cylindrical blind micro-holes) effectively diminishes the second-mode growth rate in accordance with the predictions of linear stability theory, while weakly affecting acoustic waves. The coating end effects, associated with junctures between solid and porous surfaces, are investigated.

We propose a theory of a steady circular hydraulic jump based on the shallow-water model obtained from the depth-averaged Navier–Stokes equations. The flow structure both upstream and downstream of the jump is determined by considering the flow over a plate of finite radius. The radius of the jump is found using the far-field conditions together with the jump conditions that include the effects of surface tension. We show that a steady circular hydraulic jump does not exist if the surface tension is above a certain critical value. The solution of the problem provides a basis for the hydrodynamic stability analysis of the hydraulic jump. An analogy between the hydraulic jump and a detonation wave is pointed out.

We present a combined theoretical and computational analysis of three-dimensional unsteady finite-Reynolds-number flows in collapsible tubes whose walls perform prescribed high-frequency oscillations which resemble those typically observed in experiments with a Starling resistor. Following an analysis of the flow fields, we investigate the system's overall energy budget and establish the critical Reynolds number, Recrit, at which the wall begins to extract energy from the flow. We conjecture that Recrit corresponds to the Reynolds number beyond which collapsible tubes are capable of performing sustained self-excited oscillations. Our computations suggest a simple functional relationship between Recrit and the system parameters, and we present a scaling argument to explain this observation. Finally, we demonstrate that, within the framework of the instability mechanism analysed here, self-excited oscillations of collapsible tubes are much more likely to develop from steady-state configurations in which the tube is buckled non-axisymmetrically, rather than from axisymmetric steady states, which is in agreement with experimental observations.

A mathematical model is presented for steady fluid flow across microvessel walls through a serial pathway consisting of the endothelial surface glycocalyx and the intercellular cleft between adjacent endothelial cells, with junction strands and their discontinuous gaps. The three-dimensional flow through the pathway from the vessel lumen to the tissue space has been computed numerically based on a Brinkman equation with appropriate values of the Darcy permeability. The predicted values of the hydraulic conductivity Lp, defined as the ratio of the flow rate per unit surface area of the vessel wall to the pressure drop across it, are close to experimental measurements for rat mesentery microvessels. If the values of the Darcy permeability for the surface glycocalyx are determined based on the regular arrangements of fibres with 6 nm radius and 8 nm spacing proposed recently from the detailed structural measurements, then the present study suggests that the surface glycocalyx could be much less resistant to flow compared to previous estimates by the one-dimensional flow analyses, and the intercellular cleft could be a major determinant of the hydraulic conductivity of the microvessel wall.

The motion of a vapour bubble in a subcooled liquid is studied numerically assuming axial symmetry but allowing the surface to deform under the action of the fluid dynamic stress. The flattening of the bubble in the plane orthogonal to the translational velocity increases the added mass and slows it down, while, at the same time, the decreasing volume tends to increase the velocity. The deformation of the interface also increases the surface area exposed to the incoming cooler liquid. The competition among these opposing processes is subtle and the details of the condensation cannot be captured by simpler models, two of which are considered. In spite of these differences, the estimate of the total collapse time given by a spherical model is close to that of the deforming bubble model for the cases studied. In addition to an isothermal liquid, some examples in which the bubble encounters warmer and colder liquid regions are shown.

Velocity measurements were performed in a wing-tip vortex wandering in free-stream turbulence using two four-wire hot-wire probes. Vortex wandering was well represented by a bi-normal probability density with increasing free-stream turbulence resulting in increased amplitude of wandering. The most dominant wavelength of wandering was found to remain unaffected by free-stream conditions. Two-point velocity measurements were used to reconstruct the vortex velocity profile in a frame of reference wandering with the vortex. Increasing turbulence intensity was found to increase the rate of decay of the vortex peak circumferential velocity while the radial location of this peak velocity remained unchanged. These results are consistent with several possible vortex decay mechanisms, including the stripping of vorticity by azimuthally aligned vortical structures, transfer of angular momentum from the vortex to these structures during their formation and the deformation and breakup of the vortex by strong free-stream eddies.

Accurate numerical computations of the onset of thermal convection in wide rotating spherical shells are presented. Low-Prandtl-number (σ) fluids, and non-slip boundary conditions are considered. It is shown that at small Ekman numbers (E), and very low σ values, the well-known equatorially trapped patterns of convection are superseded by multicellular outer-equatorially-attached modes. As a result, the convection spreads to higher latitudes affecting the body of the fluid, and increasing the internal viscous dissipation. Then, from E < 10−5, the critical Rayleigh number (Rc) fulfils a power-law dependence Rc ~ E−4/3, as happens for moderate and high Prandtl numbers. However, the critical precession frequency (|ωc|) and the critical azimuthal wavenumber (mc) increase discontinuously, jumping when there is a change of the radial and latitudinal structure of the preferred eigenfunction. In addition, the transition between spiralling columnar (SC), and outer-equatorially-attached (OEA) modes in the (σ, E)-space is studied. The evolution of the instability mechanisms with the parameters prevents multicellular modes being selected from σ≳0.023. As a result, and in agreement with other authors, the spiralling columnar patterns of convection are already preferred at the Prandtl number of the liquid metals. It is also found that, out of the rapidly rotating limit, the prograde antisymmetric (with respect to the equator) modes of small mc can be preferred at the onset of the primary instability.

We study the transition from laminar flow to fully developed turbulence for an inertially driven von Kármán flow between two counter-rotating large impellers fitted with curved blades over a wide range of Reynolds number (102–106). The transition is driven by the destabilization of the azimuthal shear layer, i.e. Kelvin–Helmholtz instability, which exhibits travelling/drifting waves, modulated travelling waves and chaos before the emergence of a turbulent spectrum. A local quantity – the energy of the velocity fluctuations at a given point – and a global quantity – the applied torque – are used to monitor the dynamics. The local quantity defines a critical Reynolds number Rec for the onset of time-dependence in the flow, and an upper threshold/crossover Ret for the saturation of the energy cascade. The dimensionless drag coefficient, i.e. the turbulent dissipation, reaches a plateau above this finite Ret, as expected for ‘Kolmogorov’-like turbulence for Re→∞. Our observations suggest that the transition to turbulence in this closed flow is globally supercritical: the energy of the velocity fluctuations can be considered as an order parameter characterizing the dynamics from the first laminar time-dependence to the fully developed turbulence. Spectral analysis in the temporal domain, moreover, reveals that almost all of the fluctuation energy is stored in time scales one or two orders of magnitude slower than the time scale based on impeller frequency.

An incompressibility approximation is formulated for isentropic motions in a compressible stratified fluid by defining a pseudo-density ρ* and enforcing mass conservation with respect to ρ* instead of the true density. Using this approach, sound waves will be eliminated from the governing equations provided ρ* is an explicit function of the space and time coordinates and of entropy. By construction, isentropic pressure perturbations have no influence on the pseudo-density.

A simple expression for ρ* is available for perfect gases that allows the approximate mass conservation relation to be combined with the unapproximated momentum and thermodynamic equations to yield a closed system with attractive energy conservation properties. The influence of pressure on the pseudo-density, along with the explicit (x,t) dependence of ρ* is determined entirely by the hydrostatically balanced reference state.

Scale analysis shows that the pseudo-incompressible approximation is applicable to motions for which 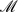2 ≪ min(1,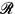2, where 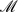is the Mach number and 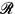the Rossby number. This assumption is easy to satisfy for small-scale atmospheric motions in which the Earth's rotation may be neglected and is also satisfied for quasi-geostrophic synoptic-scale motions, but not planetary-scale waves. This scaling assumption can, however, be relaxed to allow the accurate representation of planetary-scale motions if the pressure in the time-evolving reference state is computed with sufficient accuracy that the large-scale components of the pseudo-incompressible pressure represent small corrections to the total pressure, in which case the full solution to both the pseudo-incompressible and reference-state equations has the potential to accurately model all non-acoustic atmospheric motions.

The effects of harmonically oscillating the inner cylinder about a zero mean rotation in a Taylor–Couette flow are investigated experimentally and numerically. The resulting time-modulated circular Couette flow possesses a Z2 spatio-temporal symmetry which gives rise to two distinct modulated Taylor vortex flows. These flows are initiated at synchronous bifurcations, have the same spatial symmetries, but are characterized by different spatio-temporal symmetries and axial wavenumber. Mode competition between these two states has been investigated in the region where they bifurcate simultaneously. In the idealized numerical model, the two flows have been found to coexist and be stable in a narrow region of parameter space. However, in the physical experiment, neither state has been observed in the coexistence region. Instead, we observe noise-sustained flows with irregular time-dependent axial wavenumber. Movies are available with the online version of the paper.

Energy amplification in channel flows of Oldroyd-B fluids is studied from an input–output point of view by analysing the ensemble-average energy density associated with the velocity field of the linearized governing equations. The inputs consist of spatially distributed and temporally varying body forces that are harmonic in the streamwise and spanwise directions and stochastic in the wall-normal direction and in time. Such inputs enable the use of powerful tools from linear systems theory that have recently been applied to analyse Newtonian fluid flows. It is found that the energy density increases with a decrease in viscosity ratio (ratio of solvent viscosity to total viscosity) and an increase in Reynolds number and elasticity number. In most of the cases, streamwise-constant perturbations are most amplified and the location of maximum energy density shifts to higher spanwise wavenumbers with an increase in Reynolds number and elasticity number and a decrease in viscosity ratio. For similar parameter values, the maximum in the energy density occurs at a higher spanwise wavenumber for Poiseuille flow, whereas the maximum energy density achieves larger maxima for Couette flow. At low Reynolds numbers, the energy density decreases monotonically when the elasticity number is sufficiently small, but shows a maximum when the elasticity number becomes sufficiently large, suggesting that elasticity can amplify disturbances even when inertial effects are weak.

Observations have been made of the time-mean velocity profile at midspan in the near-wake of circular cylinders at moderate Reynolds numbers between 600 and 4600, well beyond the Reynolds number of approximately 200 at which the wake becomes three-dimensional. The measured profiles are found to be represented quite accurately by a family of function profiles with known linear instability characteristics. The complex instability frequency is then determined as a function of wake position, using the function profiles. In general, the near wake undergoes a transition from convective to absolute instability; the distance downstream to the point of transition is found to increase over the Reynolds number range investigated. The emergence of a significant region of convective instability is consistent with the known appearance of Bloor–Gerrard vortices. The selected frequency of the wake instability is determined by the saddle-point criterion; the Strouhal numbers for Bénard–von Kármán vortex shedding are found to compare well with the values in the literature.