Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-21T15:55:38.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady bubble rise and deformation in Newtonian and viscoplastic fluids and conditions for bubble entrapment

Published online by Cambridge University Press:  25 April 2008

J. TSAMOPOULOS ,
Y. DIMAKOPOULOS ,
N. CHATZIDAI ,
G. KARAPETSAS  and
M. PAVLIDIS
J. TSAMOPOULOS
Affiliation:
Laboratory of Computational Fluid Dynamics, Department of Chemical EngineeringUniversity of Patras, Patras 26500, Greece
Y. DIMAKOPOULOS
Affiliation:
Laboratory of Computational Fluid Dynamics, Department of Chemical EngineeringUniversity of Patras, Patras 26500, Greece
N. CHATZIDAI
Affiliation:
Laboratory of Computational Fluid Dynamics, Department of Chemical EngineeringUniversity of Patras, Patras 26500, Greece
G. KARAPETSAS
Affiliation:
Laboratory of Computational Fluid Dynamics, Department of Chemical EngineeringUniversity of Patras, Patras 26500, Greece
M. PAVLIDIS
Affiliation:
Laboratory of Computational Fluid Dynamics, Department of Chemical EngineeringUniversity of Patras, Patras 26500, Greece
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the buoyancy-driven rise of a bubble in a Newtonian or a viscoplastic fluid assuming axial symmetry and steady flow. Bubble pressure and rise velocity are determined, respectively, by requiring that its volume remains constant and its centre of mass remains fixed at the centre of the coordinate system. The continuous constitutive model suggested by Papanastasiou is used to describe the viscoplastic behaviour of the material. The flow equations are solved numerically using the mixed finite-element/Galerkin method. The nodal points of the computational mesh are determined by solving a set of elliptic differential equations to follow the often large deformations of the bubble surface. The accuracy of solutions is ascertained by mesh refinement and predictions are in very good agreement with previous experimental and theoretical results for Newtonian fluids. We determine the bubble shape and velocity and the shape of the yield surfaces for a wide range of material properties, expressed in terms of the Bingham Bn=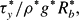 Bond Bo = 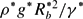and Archimedes Ar= numbers, where ρ* is the density, μ*o the viscosity, γ* the surface tension and τ*y the yield stress of the material, g* the gravitational acceleration and R*b the radius of a spherical bubble of the same volume. If the fluid is viscoplastic, the material will not be deforming outside a finite region around the bubble and, under certain conditions, it will not be deforming either behind it or around its equatorial plane in contact with the bubble. As Bn increases, the yield surfaces at the bubble equatorial plane and away from the bubble merge and the bubble becomes entrapped. When Bo is small and the bubble cannot deform from the spherical shape the critical Bn is 0.143, i.e. it is a factor of 3/2 higher than the critical Bn for the entrapment of a solid sphere in a Bingham fluid, in direct correspondence with the 3/2 higher terminal velocity of a bubble over that of a sphere under the same buoyancy force in Stokes flow. As Bo increases allowing the bubble to squeeze through the material more easily, the critical Bingham number increases as well, but eventually it reaches an asymptotic value. Ar affects the critical Bn value much less.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 601 , 25 April 2008 , pp. 123 - 164
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Astarista, G. & Apuzzo, G. 1965 Motion of gas bubbles in non–Newtonian liquids. AIChE J. 11, 815–820.CrossRefGoogle Scholar
Bercovier, M. & Engelman, M. 1980 A finite element method for the incompressible non-Newtonian flows. J. Comput. Phys. 36, 313–326.Google Scholar
Beris, A. N., Tsamopoulos, J. A., Armstrong, R. C. & Brown, R. A. 1985 Creeping motion of a sphere through a Bingham plastic. J. Fluid Mech. 158, 219–244.Google Scholar
Bhaga, D. & Weber, M. E. 1981 Bubbles in viscous liquids: shapes, wakes and velocities. J. Fluid Mech. 105, 61–85.Google Scholar
Bingham, E. C. 1922 Fluidity and Plasticity. McGraw-Hill.Google Scholar
Blackery, J. & Mitsoulis, E. 1997 Creeping motion of a sphere in tubes filled with a Bingham plastic material. J. Non-Newtonian Fluid Mech. 70, 59–77.Google Scholar
Blanco, A. & Magnaudet, J. 1995 The structure of the axisymmetric high-Reynolds number flow around an ellipsoidal bubble of fixed shape. Phys. Fluids 7, 1265–1274.Google Scholar
Bonometti, T. & Magnaudet, J. 2006 Transition from spherical cap to toroidal bubbles. Phys. Fluids 18, 052102 1–12.Google Scholar
Bonometti, T. & Magnaudet, J. 2007 An interface capturing method for incompressible two phase flows validation and application to bubble dynamics. Intl. J. Multiphase Flow 33, 109–133.Google Scholar
Burgos, G. R., Alexandrou, A. N. & Entov, N. M. 1999 On the determination of yield surfaces in Herschel-Bulkley fluids. J. Rheol. 43, 463–483.Google Scholar
Christov, C. I. & Volkov, P. K. 1985 Numerical investigation of the steady viscous flow past a stationary deformable bubble. J. Fluid Mech. 158, 341–364.CrossRefGoogle Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic.Google Scholar
Dimakopoulos, Y. & Tsamopoulos, J. 2003 a Transient displacement of a viscoplastic material by air in straight and suddenly constricted tubes. J. Non-Newtonian Fluid Mech. 112, 43–75.Google Scholar
Dimakopoulos, Y. & Tsamopoulos, J. 2003 b A quasi-elliptic transformation for moving boundary problems with large anisotropic deformations. J. Comput. Phys. 192, 494–522.CrossRefGoogle Scholar
Dimakopoulos, Y. & Tsamopoulos, J. 2003 c Transient displacement of a Newtonian fluid by air in straight or suddenly constricted tubes. Phys. Fluids 15, 1973–1991.CrossRefGoogle Scholar
Dimakopoulos, Y. & Tsamopoulos, J. 2004 On the gas-penetration in straight tubes completely filled with a viscoelastic fluid. J. Non-Newtonian Fluid Mech. 117, 117–139.CrossRefGoogle Scholar
Dimakopoulos, Y. & Tsamopoulos, J. 2006 Transient displacement of Newtonian and viscoplastic liquid by air in complex tubes. J. Non-Newtonian Fluid Mech. doi:10.1016/j.jnnfm.2006.08.002.Google Scholar
Dubash, N. & Frigaard, I. 2004 Conditions for static bubbles in viscoplastic fluids. Phys. Fluids 16, 4319–4330.CrossRefGoogle Scholar
Dubash, N. & Frigaard, I. 2007 Propagation and stopping of air bubbles in Carbopol solutions. J. Non-Newtonian Fluid Mech. 142, 123–134.Google Scholar
Duineveld, P. 1995 The rise velocity and shape of bubbles in pure water at high Reynolds number. J. Fluid Mech. 292, 325–332.Google Scholar
Foteinopoulou, K., Mavrantzas, V., Dimakopoulos, Y. & Tsamopoulos, J. 2006 Numerical simulation of multiple bubbles growing in a Newtonian liquid filament undergoing stretching. Phys. Fluids 18, 042106.CrossRefGoogle Scholar
Frigaard, I. & Nouar, C. 2005 On the usage of viscosity regularization methods for visco-plastic fluid flow computation. J. Non-Newtonian Fluid Mech. 127, 1–26.CrossRefGoogle Scholar
Glowinski, R., Lions, J. & Trémolières, R. 1981 Numerical Analysis of Variational Inequalities, North-Holland.Google Scholar
Gueslin, B., Talini, L., Herzhaft, B., Peysson, Y. & Allain, C. 2006 Flow induced by a sphere settling in an aging yield-stress fluid. Phys. Fluids 18, 103101.Google Scholar
Haberman, W. L. & Morton, R. K. 1953 An experimental investigation of the drag and shape of air bubbles rising in various liquids. Report 802, Navy Dept., David W. Taylor Model Basin. 68 Washington, DC.Google Scholar
Hadamard, J. S. 1911 Mouvement permanent lent d'une sphère liquide et visqueuse dans un liquide visqueux. C. R. l'Acad. Sci. Paris 152, 1735–1738.Google Scholar
Harper, J. F. 1972 The motion of bubbles and drops through liquids. Adv. Appl. Mech. 12, 59–129.CrossRefGoogle Scholar
Hnat, J. G. & Buckmaster, J. D. 1976 Spherical cap bubbles and skirt formation. Phys. Fluids 19, 182–194.CrossRefGoogle Scholar
Hua, J. & Lou, J. 2007 Numerical simulation of bubble rising in viscous liquid. J. Comput. Phys. 222, 769–795.CrossRefGoogle Scholar
Johnson, A. & White, D. B. 1991 Gas-rise velocities during kicks. SPE Drilling Engineering, 6, 257–263, and Society of Petroleum Engineers Paper 20431.Google Scholar
Karapetsas, G. & Tsamopoulos, J. 2006 Transient squeeze flow of viscoplastic materials. J. Non-Newtonian Fluid Mech. 133, 35–56.Google Scholar
Koh, C. & Leal, L. G. 1989 The stability of drop shapes for transition at zero Reynolds number through a quiescent fluid. Phys. Fluids A 1, 1309–1313.Google Scholar
Levich, V. G. 1949 The motion of bubbles at high Reynolds numbers. Zh. Eksper. Teor. Fiz. 19, 18–24.Google Scholar
Liu, B. T., Muller, S. & Denn, M. M. 2002 Convergence of a regularization method for creeping flow of a Bingham material about a rigid sphere, J. Non-Newtonian Fluid Mech. 102, 179–191.Google Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32, 659–708.Google Scholar
Malaga, C. & Rallison, J. M. 2007 A rising bubble in a polymer solution. J. Non-Newtonian Fluid Mech. 141, 59–78.Google Scholar
Maxworthy, T., Gnann, C., Kurten, M. & Durst, F. 1996 Experiments on the rise of air bubbles in clean viscous liquids. J. Fluid Mech. 321, 421–441.CrossRefGoogle Scholar
Miksis, M. J., Vanden-Broeck, J. M. & Keller, J. B. 1982 Rising bubbles. J. Fluid Mech. 123, 31–41.Google Scholar
Moore, D. W. 1963 The boundary layer on a spherical gas bubble. J. Fluid Mech. 16, 161–176.CrossRefGoogle Scholar
Moore, D. W. 1965 The velocity of rise of distorted gas bubbles in a liquid of small viscosity. J. Fluid Mech. 23, 749–766.CrossRefGoogle Scholar
Papanastasiou, T. C. 1987 Flows of materials with yield. J. Rheol. 31, 385–404.CrossRefGoogle Scholar
Pilz, C. & Benn, G. 2007 On the critical bubble volume at the rise velocity jump discontinuity in viscoelastic liquids. J. Non-Newtonian Fluid Mech. 145, 124–138.CrossRefGoogle Scholar
Rybczyński, W. 1911 On the translatory motion of fluid sphere in a viscous medium. Bull. Intl l' Acad. Polonaise Scie. Lett. Classe des Sciences Mathématiques et Naturelles A, 40–46.Google Scholar
Ryskin, G. & Leal, L. G. 1984 Numerical solution of free-boundary problems in fluid mechanics. Part 2. Buoyancy-driven motion of a gas bubble through a quiescent liquid. J. Fluid Mech. 148, 19–35.CrossRefGoogle Scholar
Schenk, O. & Gärtner, K. 2004 Solving unsymmetric sparse systems of linear equations with PARDISO. J. Future Generations Computer Systems 20, 475–487.Google Scholar
Schenk, O. & Gärtner, K. 2006 On fast factorization pivoting methods for symmetric indefinite systems. Elec. Trans. Numer. Anal. 23, 158–179.Google Scholar
Smyrnaios, D. & Tsamopoulos, J. 2001 Squeeze flow of Bingham plastics. J. Non-Newtonian Fluid Mech. 100, 165–190.CrossRefGoogle Scholar
Stein, S. & Buggisch, H. 2000 Rise of pulsating bubble in fluids with a yield stress. Z. Angew. Math. Mech. 11–12, 827–834.Google Scholar
Taylor, T. & Acrivos, A. 1964 On the deformation and drag of a falling drop at low Reynolds number. J. Fluid Mech. 18, 466–476.Google Scholar
Terasaka, K. & Tsuge, H. 2001 Bubble formation at a nozzle submerged in viscous liquids having yield stress. Chem. Engng Sci. 56, 3237–3245.Google Scholar
Unverdi, S. O. & Tryggvason, G. 1992 A front tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 100, 25–37.CrossRefGoogle Scholar