We consider the problem of a rigid plate, inclined at an angle 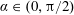 $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$ to the horizontal, accelerating uniformly from rest into, or away from, a semi-infinite strip of inviscid, incompressible fluid under gravity. Following on from Gallagher et al. (J. Fluid Mech., vol. 841, 2018, pp. 109–145) (henceforth referred to as GNB), it is of interest to analyse the well-posedness and stability of the principal flow with respect to perturbations in the initially horizontal free surface close to the plate contact point. In particular we find that the solution to the principal unperturbed problem, denoted by [IBVP] in GNB, is well-posed and stable with respect to perturbations in initial data in the region of interest, localised close to the contact point of the free surface and the plate, when the plate is accelerated with dimensionless acceleration
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$ to the horizontal, accelerating uniformly from rest into, or away from, a semi-infinite strip of inviscid, incompressible fluid under gravity. Following on from Gallagher et al. (J. Fluid Mech., vol. 841, 2018, pp. 109–145) (henceforth referred to as GNB), it is of interest to analyse the well-posedness and stability of the principal flow with respect to perturbations in the initially horizontal free surface close to the plate contact point. In particular we find that the solution to the principal unperturbed problem, denoted by [IBVP] in GNB, is well-posed and stable with respect to perturbations in initial data in the region of interest, localised close to the contact point of the free surface and the plate, when the plate is accelerated with dimensionless acceleration 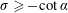 $\unicode[STIX]{x1D70E}\geqslant -\cot \,\unicode[STIX]{x1D6FC}$, while the solution to [IBVP] is ill-posed with respect to such perturbations in the initial data, when the plate is accelerated with dimensionless acceleration
$\unicode[STIX]{x1D70E}\geqslant -\cot \,\unicode[STIX]{x1D6FC}$, while the solution to [IBVP] is ill-posed with respect to such perturbations in the initial data, when the plate is accelerated with dimensionless acceleration 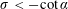 $\unicode[STIX]{x1D70E}<-\cot \,\unicode[STIX]{x1D6FC}$. The physical source of the ill-posedness of the principal problem [IBVP], when
$\unicode[STIX]{x1D70E}<-\cot \,\unicode[STIX]{x1D6FC}$. The physical source of the ill-posedness of the principal problem [IBVP], when 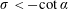 $\unicode[STIX]{x1D70E}<-\cot \,\unicode[STIX]{x1D6FC}$, is revealed to be due to the leading-order problem in the innermost region localised close to the initial contact point being in the form of a local Rayleigh–Taylor problem. As a consequence of this mechanistic interpretation we anticipate that, when the plate is accelerated with
$\unicode[STIX]{x1D70E}<-\cot \,\unicode[STIX]{x1D6FC}$, is revealed to be due to the leading-order problem in the innermost region localised close to the initial contact point being in the form of a local Rayleigh–Taylor problem. As a consequence of this mechanistic interpretation we anticipate that, when the plate is accelerated with 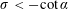 $\unicode[STIX]{x1D70E}<-\cot \,\unicode[STIX]{x1D6FC}$, the inclusion of weak surface tension effects will restore well-posedness of the problem [IBVP] which will, however, remain temporally unstable.
$\unicode[STIX]{x1D70E}<-\cot \,\unicode[STIX]{x1D6FC}$, the inclusion of weak surface tension effects will restore well-posedness of the problem [IBVP] which will, however, remain temporally unstable.