Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T06:40:52.937Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent boundary-layer flow beneath a vortex. Part 2. Power-law swirl

Published online by Cambridge University Press:  03 April 2020

David E. Loper Open the ORCID record for David E. Loper [Opens in a new window]
David E. Loper*
Affiliation:
Professor Emeritus, Florida State University, Tallahassee, FL32306, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

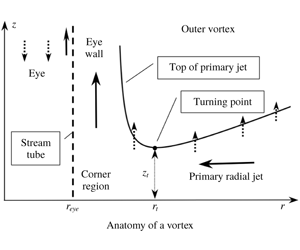
The problem formulated in Part 1 (Loper, J. Fluid Mech., vol. 892, 2020, A16) for flow in the turbulent boundary layer beneath a vortex is solved for a power-law swirl: $v_{\infty }(r)\sim r^{2\unicode[STIX]{x1D703}-1}$, where $r$ is cylindrical radius and $\unicode[STIX]{x1D703}$ is a constant parameter, with turbulent diffusivity parameterized as $\unicode[STIX]{x1D708}=v_{\infty }L$ and the diffusivity function $L$ either independent of axial distance $z$ from a stationary plane (model A) or constant within a rough layer of thickness $z_{0}$ adjoining the plane and linear in $z$ outside (model B). Model A is not a useful model of vortical flow, whereas model B produces realistic results. As found in Part 1 for $\unicode[STIX]{x1D703}=1.0$, radial flow consists of a sequence jets having thicknesses that vary nearly linearly with $r$. A novel structural feature is the turning point $(r_{t},z_{t})$, where the primary jet has a minimum height. The radius $r_{t}$ is a proxy for the eye radius of a vortex and $z_{t}$ is a proxy for the size of the corner region. As $r$ decreases from $r_{t}$, the primary jet thickens, axial outflow from the layer increases and axial oscillations become larger, presaging a breakdown of the boundary layer. For small $\unicode[STIX]{x1D703}$, $r_{t}\sim z_{0}/\unicode[STIX]{x1D716}\unicode[STIX]{x1D703}$ and $z_{t}\sim z_{0}/\unicode[STIX]{x1D703}^{3/2}$. The lack of existence of the turning point for $\unicode[STIX]{x1D703}\gtrsim 0.42$ and the acceleration of the turning point away from the origin of the meridional plane as $\unicode[STIX]{x1D703}\rightarrow 0$ provide partial explanations why weakly swirling flows do not have eyes, why strongly swirling flows have eyes and why a boundary layer cannot exist beneath a potential vortex.

JFM classification

Boundary Layers: Boundary layer structure Geophysical and Geological Flows: Atmospheric flows Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 892 , 10 June 2020 , A17
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bak, P. 1996 How Nature Works, p. 212. Springer.CrossRefGoogle Scholar
Bĕlík, P., Dokken, D. P., Schloz, K. & Shvartsman, M. M. 2014 Fractal powers in Serrin’s swirling vortex solutions. Asymptotic Solutions 90, 53–82.CrossRefGoogle Scholar
Bödewadt, U. T. 1940 Die drehströmung über festum grund. Z. Angew. Math. Mech. 20, 241–253.CrossRefGoogle Scholar
Eliassen, A. 1971 On the Ekman layer in a circular vortex. J. Met. Soc. Japan 49, 784–789.CrossRefGoogle Scholar
Karstens, C. D., Gallus, W. A. Jr, Lee, B. D. & Finley, C. A. 2013 Analysis of tornado-induced tree fall using aerial photography from the Joplin, Missouri, and Tuscaloosa-Birmingham, Alabama, tornadoes of 2011. J. Appl. Meterol. Climatology 52, 1049–1068.CrossRefGoogle Scholar
Kepert, J. D. 2010a Slab- and height-resolving models of the tropical cyclone boundary layer. Part I. Comparing the simulations. Q. J. R. Meterol. Soc. 136, 1686–1699.CrossRefGoogle Scholar
Kepert, J. D. 2010b Slab- and height-resolving models of the tropical cyclone boundary layer. Part II. Why the simulations differ. Q. J. R. Meterol. Soc. 136, 1700–1711.CrossRefGoogle Scholar
Loper, D. E. 2017 Geophysical Waves and Flows: Theory and Application in the Atmosphere, Hydrosphere and Geosphere, p. 505. Cambridge University Press.CrossRefGoogle Scholar
Loper, D. E. 2020 Turbulent boundary-layer flow beneath a vortex. Part 1. Turbulent Bödewadt flow. J. Fluid Mech. 892, A16.Google Scholar
Mallen, K. J., Montgomery, M. T. & Wang, B. 2005 Reexamining the near-core radial structure of the tropical cyclone primary circulation: implications for vortex resiliency. J. Atmos. Sci. 62, 408–425.CrossRefGoogle Scholar
Nolan, D. S., Dahl, N. A., Bryan, G. H. & Rotunno, R. 2017 Tornado vortex structure, intensity, and surface wind gusts in large-eddy simulations with fully developed turbulence. J. Atmos. Sci. 74, 1573–1597.CrossRefGoogle Scholar
Oruba, L., Davidson, P. A. & Dormy, E. 2017 Eye formation in rotating convection. J. Fluid Mech. 812, 890–904.CrossRefGoogle Scholar
Oruba, L., Davidson, P. A. & Dormy, E. 2018 Formation of eyes in large-scale cyclonic vortices. Phys. Ref. Fluids 3, 013502.Google Scholar
Pearce, R. 2005 Why must hurricanes have eyes? Weather 60, 19–24.CrossRefGoogle Scholar
Schlichting, H. 1968 Boundary Layer Theory, p. 747. McGraw Hill.Google Scholar
Smith, R. K. 1980 Tropical cyclone eye dynamics. J. Atmos. Sci. 37, 1227–1232.2.0.CO;2>CrossRefGoogle Scholar
Smith, R. K. 2005 Why must hurricanes have eyes? – Revisited. Weather 60, 326–328.CrossRefGoogle Scholar
Wurman, J. & Alexander, C. R. 2005 The 30 May 1998 Spencer, South Dakota, storm. Part II. Comparison of observed damage and radar-derived winds in the tornadoes. Mon. Weath. Rev. 133, 97–119.CrossRefGoogle Scholar
Wurman, J. & Gill, S. 2000 Finescale radar observations of the Dimmitt, Texas (2 June 1995), Tornado. Mon. Weath. Rev. 128, 2135–2164.2.0.CO;2>CrossRefGoogle Scholar