A mono-energetic electron plasma is trapped in a one-dimensional parabolic potential well. In the undisturbed state a suitable background charge provides space-charge neutrality. It is shown that stationary disturbances of infinitesimal amplitude can exist in the plasma for certain critical values of the parameter 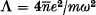 $\Lambda \,=\,{4\bar{n}{{e}^{2}}}/{m{{\omega }^{2}}}\;\$, where
$\Lambda \,=\,{4\bar{n}{{e}^{2}}}/{m{{\omega }^{2}}}\;\$, where 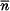 $\bar{n}\$ is the mean electron density and ω/2π is the frequency of oscillation of the electrons in the well. The first few critical values are Λ = 0, 4·12, 8·2.
$\bar{n}\$ is the mean electron density and ω/2π is the frequency of oscillation of the electrons in the well. The first few critical values are Λ = 0, 4·12, 8·2.
The boundary conditions at the end of the plasma are non-linear. As a result stationary disturbances of finite amplitude in a given mode, say the rth, require that Λ shall exceed Λr. Further it can be shown that disturbances of small amplitude in the rth mode are unstable when Λ exceeds Λr. This applies even for Λr = 0; in this case there exist nearby an unstable even and an unstable odd mode.
It seems likely that these results can be extended to all cases in which the potential well is symmetrical.