Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-19T13:51:06.147Z Has data issue: false hasContentIssue false
  • English
  • Français

Upward versus downward non-Boussinesq turbulent fountains

Published online by Cambridge University Press:  21 March 2019

Samuel Vaux Open the ORCID record for Samuel Vaux [Opens in a new window] ,
Rabah Mehaddi ,
Olivier Vauquelin Open the ORCID record for Olivier Vauquelin [Opens in a new window]  and
Fabien Candelier
Samuel Vaux*
Affiliation:
Institut de Radioprotection et de Sûreté Nucléaire (IRSN), PSN-RES, SA2I, LIE, Cadarache, 13115 St Paul-lez-Durance, France
Rabah Mehaddi
Affiliation:
Université de Lorraine, CNRS, LEMTA UMR 7563, 54518 Vandoeuvre-lès-Nancy, France
Olivier Vauquelin
Affiliation:
Aix-Marseille Université, CNRS, IUSTI UMR 7343, 13013 Marseille, France
Fabien Candelier
Affiliation:
Aix-Marseille Université, CNRS, IUSTI UMR 7343, 13013 Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Turbulent miscible fountains discharged vertically from a round source into quiescent uniform unbounded environments of density 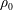$\unicode[STIX]{x1D70C}_{0}$ are investigated numerically using large-eddy simulations. Both upward and downward fountains are considered. The numerical simulations cover a wide range of the density ratio 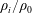$\unicode[STIX]{x1D70C}_{i}/\unicode[STIX]{x1D70C}_{0}$, where 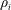$\unicode[STIX]{x1D70C}_{i}$ is the source density of the released fluid. These simulations are used to evaluate how the initial maximum height 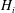$H_{i}$ and the steady state height 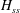$H_{ss}$ of the fountains are affected by large density contrasts, i.e. in the general non-Boussinesq case. For both upward and downward non-Boussinesq fountains, the ratio 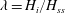$\unicode[STIX]{x1D706}=H_{i}/H_{ss}$ remains close to 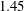$1.45$, as usually observed for Boussinesq fountains. However the Froude (linear) scaling originally introduced by Turner (J. Fluid Mech., vol. 26 (4), 1966, pp. 779–792) for Boussinesq fountains is no longer valid to determine the steady fountain height. The ratio between 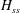$H_{ss}$ and the height predicted by the Turner’s relation turns out to be proportional to 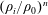$(\unicode[STIX]{x1D70C}_{i}/\unicode[STIX]{x1D70C}_{0})^{n}$. Remarkably, it is found that the power exponent $n$ differs following the direction in which the buoyant fluid is released (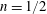$n=1/2$ for downward fountains and 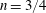$n=3/4$ for upward fountains). This new result demonstrates that for non-Boussinesq turbulent fountains the configurations heavy/light and light/heavy are not equivalent. Finally, scalings are proposed for fountains, regardless of the direction (upwards and downwards) and of the density difference (Boussinesq and non-Boussinesq).

JFM classification

Convection: Plumes/thermals
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 374 - 391
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baddour, R. E. & Zhang, H. 2009 Density effect on round turbulent hypersaline fountain. J. Hydraul. Engng ASCE 135 (1), 57–59.Google Scholar
Baines, W. D., Turner, J. S. & Campbell, I. H. 1990 Turbulent fountains in an open chamber. J. Fluid Mech. 212, 557–592.Google Scholar
Bloomfield, L. J. & Kerr, R. C. 2000 A theoretical model of a turbulent fountain. J. Fluid Mech. 424, 197–216.Google Scholar
Van den Bremer, T. S. & Hunt, G. R. 2010 Universal solutions for Boussinesq and non-Boussinesq plumes. J. Fluid Mech. 644, 165–192.Google Scholar
Bruneau, C.-H. 2000 Boundary conditions on artificial frontiers for incompressible and compressible Navier–Stokes equations. Math. Modelling Numer. Anal. 34, 303–314.Google Scholar
Bruneau, C.-H. & Fabrie, P. 1994 Effective downstream boundary conditions for incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 19, 693–705.Google Scholar
Bruneau, C.-H. & Fabrie, P. 1996 New efficient boundary conditions for incompressible Navier–Stokes equations: a well-posedness result. Math. Modelling Numer. Anal. 30, 815–840.Google Scholar
Burridge, H. C. & Hunt, G. R. 2012 The rise heights of low- and high-Froude-number turbulent axisymmetric fountains. J. Fluid Mech. 691, 392–416.Google Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2008 On the dynamics of volcanic columns: a comparison of field data with a new model of negatively buoyant jets. J. Volcanol. Geotherm. Res. 178 (1), 94–103.Google Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2010 The rise and fall of turbulent fountains: a new model for improved quantitative predictions. J. Fluid Mech. 657, 265–284.Google Scholar
Crapper, P. F. & Baines, W. D. 1978 Some remarks on non-Boussinesq forced plumes. Atmos. Environ. 12, 1939–1941.Google Scholar
Cresswell, R. W. & Szczepura, R. T. 1993 Experimental investigation into a turbulent jet with negative buoyancy. Phys. Fluids A 5 (11), 2865–2878.Google Scholar
Hermanson, J. C. & Cetegen, B. M. 2000 Shock-induced mixing of nonhomogeneous density turbulent jets. Phys. Fluids 12 (5), 1210–1225.Google Scholar
Hunt, G. R. & Burridge, H. C. 2015 Fountains in industry and nature. Annu. Rev. Fluid Mech. 47, 195–220.Google Scholar
Kaye, N. B. 2008 Turbulent plumes in stratified environments: a review of recent work. Atmos.-Ocean 46 (4), 433–441.Google Scholar
Kaye, N. B. & Hunt, G. R. 2006 Weak fountains. J. Fluid Mech. 558, 319–328.Google Scholar
Mehaddi, R., Vauquelin, O. & Candelier, F. 2015a Experimental non-Boussinesq fountains. J. Fluid Mech. 784, R6.Google Scholar
Mehaddi, R., Vaux, S., Candelier, F. & Vauquelin, O. 2015b On the modelling of steady turbulent fountains. Environ. Fluid Mech. 15 (6), 1115–1134.Google Scholar
Michaux, G. & Vauquelin, O. 2008 Solutions for turbulent buoyant plumes rising from circular sources. Phys. Fluids 20 (6), 066601.Google Scholar
Morton, B. R. 1959 Forced plumes. J. Fluid Mech. 5 (1), 151–163.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234 (1196), 1–23.Google Scholar
Nicoud, F. & Ducros, F. 1999 Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 62 (3), 183–200.Google Scholar
Pantzlaff, L. & Lueptow, R. M. 1999 Transient positively and negatively buoyant turbulent round jets. Exp. Fluids 27 (2), 117–125.Google Scholar
Papanicolaou, P. N. & Kokkalis, T. J. 2008 Vertical buoyancy preserving and non-preserving fountains, in a homogeneous calm ambient. Intl J. Heat Mass Transfer 51 (15–16), 4109–4120.Google Scholar
Ricciardi, L., Prévost, C., Bouilloux, L. & Sestier-Carlin, R. 2008 Experimental and numerical study of heavy gas dispersion in a ventilated room. J. Hazard. Mater. 152 (2), 493–505.Google Scholar
Ricou, F. P. & Spalding, D. B. 1961 Measurements of entrainment by axisymmetrical turbulent jets. J. Fluid Mech. 11 (1), 21–32.Google Scholar
Rooney, G. G. & Linden, P. F. 1996 Similarity considerations for non-Boussinesq plumes in an unstratified environment. J. Fluid Mech. 318, 237–250.Google Scholar
Seban, R. A., Behnia, M. M. & Abreu, K. E. 1978 Temperatures in a heated air jet discharged downward. Intl J. Heat Mass Transfer 21 (12), 1453–1458.Google Scholar
Turner, J. S. 1966 Jets and plumes with negative or reversing buoyancy. J. Fluid Mech. 26 (4), 779–792.Google Scholar
Williamson, N., Armfield, S. W. & Lin, W. 2010 Transition behaviour of weak turbulent fountains. J. Fluid Mech. 655, 306–326.Google Scholar
Williamson, N., Armfield, S. W. & Lin, W. 2011 Forced turbulent fountain flow behaviour. J. Fluid Mech. 671, 535–558.Google Scholar
Wu, X.-Z. & Libchaber, A. 1991 Non-boussinesq effects in free thermal convection. Phys. Rev. A 43 (6), 2833–2839.Google Scholar
Zhang, H. & Baddour, R. E. 1998 Maximum penetration of vertical round dense jets at small and large Froude numbers. J. Hydraul. Engng ASCE 124 (5), 550–553.Google Scholar
Zhou, X., Luo, K. H. & Williams, J. J. R. 2001 Large-eddy simulation of a turbulent forced plume. Eur. J. Mech. (B/Fluids) 20 (2), 233–254.Google Scholar