Published online by Cambridge University Press: 25 March 2019
Unsteady spatially localized states such as puffs, slugs or spots play an important role in transition to turbulence. In plane Couette flow, steady versions of these states are found on two intertwined solution branches describing homoclinic snaking (Schneider et al., Phys. Rev. Lett., vol. 104, 2010, 104501). These branches can be used to generate a number of spatially localized initial conditions whose transition can be investigated. From the low Reynolds numbers where homoclinic snaking is first observed (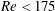 $Re<175$) to transitional ones (
$Re<175$) to transitional ones (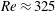 $Re\approx 325$), these spatially localized states traverse various regimes where their relaminarization time and dynamics are affected by the dynamical structure of phase space. These regimes are reported and characterized in this paper for a
$Re\approx 325$), these spatially localized states traverse various regimes where their relaminarization time and dynamics are affected by the dynamical structure of phase space. These regimes are reported and characterized in this paper for a 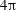 $4\unicode[STIX]{x03C0}$-periodic domain in the streamwise direction as a function of the two remaining variables: the Reynolds number and the width of the localized pattern. Close to the snaking, localized states are attracted by spatially localized periodic orbits before relaminarizing. At larger values of the Reynolds number, the flow enters a chaotic transient of variable duration before relaminarizing. Very long chaotic transients (
$4\unicode[STIX]{x03C0}$-periodic domain in the streamwise direction as a function of the two remaining variables: the Reynolds number and the width of the localized pattern. Close to the snaking, localized states are attracted by spatially localized periodic orbits before relaminarizing. At larger values of the Reynolds number, the flow enters a chaotic transient of variable duration before relaminarizing. Very long chaotic transients (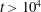 $t>10^{4}$) can be observed without difficulty for relatively low values of the Reynolds number (
$t>10^{4}$) can be observed without difficulty for relatively low values of the Reynolds number (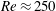 $Re\approx 250$).
$Re\approx 250$).