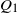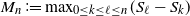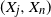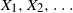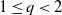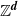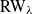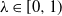Research Papers
A renewal theory approach to two-state switching problems with infinite values
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 1-18
-
- Article
- Export citation
Small-time moderate deviations for the randomised Heston model
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 19-28
-
- Article
- Export citation
Improvements on the distribution of maximal segmental scores in a Markovian sequence
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 29-52
-
- Article
- Export citation
On the occupancy problem for a regime-switching model
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 53-77
-
- Article
- Export citation
Records for time-dependent stationary Gaussian sequences
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 78-96
-
- Article
- Export citation
Generalized stacked contact process with variable host fitness
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 97-121
-
- Article
- Export citation
Directed preferential attachment models: Limiting degree distributions and their tails
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 122-136
-
- Article
- Export citation
Integral functionals under the excursion measure
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 137-155
-
- Article
- Export citation
Some new results on stochastic comparisons of coherent systems using signatures
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 156-173
-
- Article
- Export citation
Uniform asymptotic normality of weighted sums of short-memory linear processes
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 174-195
-
- Article
- Export citation
A unifying approach to branching processes in a varying environment
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 196-220
-
- Article
- Export citation
On first passage times of sticky reflecting diffusion processes with double exponential jumps
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 221-236
-
- Article
- Export citation
Branching processes in a random environment with immigration stopped at zero
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 237-249
-
- Article
- Export citation
Weak convergence of random processes with immigration at random times
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 250-265
-
- Article
- Export citation
Long-time behavior of Lévy-driven Ornstein–Uhlenbeck processes with regime switching
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 266-279
-
- Article
- Export citation
A functional limit theorem for general shot noise processes
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 280-294
-
- Article
- Export citation
An invariance principle and a large deviation principle for the biased random walk on
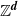 ${\mathbb{Z}}^{\lowercase{\textbf{\textit{d}}}}$
${\mathbb{Z}}^{\lowercase{\textbf{\textit{d}}}}$
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 295-313
-
- Article
- Export citation
Strong convergence of multivariate maxima
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 314-331
-
- Article
- Export citation
A model for the spreading of fake news
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 332-342
-
- Article
- Export citation
A bound on the rate of convergence in the central limit theorem for renewal processes under second moment conditions
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2020, pp. 343-360
-
- Article
- Export citation