Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T08:12:41.726Z Has data issue: false hasContentIssue false
  • English
  • Français

Martingale decomposition of an L2 space with nonlinear stochastic integrals

Part of: Stochastic processes

Published online by Cambridge University Press:  11 December 2019

Clarence Simard
Clarence Simard*
Affiliation:
Université du Québec à Montréal
*
* Postal address: Département de Mathématiques, Université du Québec à Montréal, C.P. 8888, succ. Centre-ville, Montréal (Québec), H3C 3P8, Canada.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper generalizes the Kunita–Watanabe decomposition of a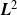n $L^2$ space. The generalization comes from using nonlinear stochastic integrals where the integrator is a family of continuous martingales bounded in 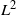$L^2$ . This result is also the solution of an optimization problem in 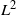$L^2$ . First, martingales are assumed to be stochastic integrals. Then, to get the general result, it is shown that the regularity of the family of martingales with respect to its spatial parameter is inherited by the integrands in the integral representation of the martingales. Finally, an example showing how the results of this paper, with the Clark–Ocone formula, can be applied to polynomial functions of Brownian integrals.

Keywords

Stochastic calculusoptimizationmartingalesorthogonal decompositionClark–Ocone formula

MSC classification

Primary: 60G44: Martingales with continuous parameter
Type
Research Papers
Information
Journal of Applied Probability , Volume 56 , Issue 4 , December 2019 , pp. 1231 - 1243
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bank, P. and Baum, D. (2004). Hedging and portfolio optimization in illiquid financial markets with a large trader. Math. Finance 14, 1–18.CrossRefGoogle Scholar
Carmona, R. and Nualart, D. (1990). Nonlinear Stochastic Integrators, Equations and Flows, Vol. 6, Stochastic Monographs. Gordon and Breach, London.Google Scholar
Cetin, U., Jarrow, R. and Protter, P. (2004). Liquidity risk and arbitrage pricing theory. Finance Stoch. 8, 311–341.CrossRefGoogle Scholar
Chitashvili, R. (1983). Martingale ideology in the theory of controlled stochastic processes. In Probability and Mathematical Statistics, eds. Prokhorov, J. V. and Itô, K., Springer, New York, pp. 73–92.CrossRefGoogle Scholar
Chitashvili, R. and Mania, M. (1996). Characterization of a regular family of semimartingales by line integrals. Georgian Math. J. 3, 525–542.CrossRefGoogle Scholar
Chitashvili, R. and Mania, M. (1999). Stochastic line integrals with respect to local martingales and semimartingales. Proc. Tbilisi A. Razmadze Math. Inst. 120, 1–26.Google Scholar
Kühn, C. (2012). Nonlinear stochastic integration with a non-smooth family of integrators. Stochastics 84, 37–53.CrossRefGoogle Scholar
Kunita, H. (1990). Stochastic Flows and Stochastic Differential Equations, Vol. 24 of Cambridge Studies in Advanced Mathematics. Cambridge University Press.Google Scholar
Kunita, H. and Watanabe, S. (1967). On square integrable martingales. Nagoya Math. J. 30, 209–245.CrossRefGoogle Scholar
Nualart, D. (2006). The Malliavin Calculus and Related Topics, 2nd edn. Springer, Berlin.Google Scholar
Schweizer, M. (1994). Approximating random variables by stochastic integrals. Ann. Prob. 22, 1536–1575.CrossRefGoogle Scholar
Williams, D. (1991). Probability with Martingales. Cambridge University Press.CrossRefGoogle Scholar