Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T13:29:38.274Z Has data issue: false hasContentIssue false
  • English
  • Français

Contact and chord length distributions of the Poisson Voronoi tessellation

Part of: Geometric probability and stochastic geometry General convexity

Published online by Cambridge University Press:  14 July 2016

Lutz Muche  and
Dietrich Stoyan
Lutz Muche
Affiliation:
Bergakademie Freiberg
Dietrich Stoyan*
Affiliation:
Bergakademie Freiberg
*
∗Postal address: Fachbereich Mathematik, Bergakademie Freiberg, DO-9200 Freiberg, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

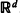This paper presents the form of some characteristics of the Voronoi tessellation which is generated by a stationary Poisson process in . Expressions are given for the spherical and linear contact distribution functions. These formulae lead to numerically tractable double-integral formulae for chord length probability density functions.

Keywords

LINEAR CONTACT DISTRIBUTIONSPHERICAL CONTACT DISTRIBUTION

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 52A22: Random convex sets and integral geometry
Type
Short Communications
Information
Journal of Applied Probability , Volume 29 , Issue 2 , June 1992 , pp. 467 - 471
Copyright
Copyright © Applied Probability Trust 1992 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boots, B. N. (1987) Voronoi (Thiessen) Polygons. Geo Books, Norwich.Google Scholar
Gilbert, E. N. (1962) Random subdivisions of space into crystals. Ann. Math. Statist. 33, 958–972.CrossRefGoogle Scholar
Miles, R. E. (1972) The random division of space. Suppl. Adv. Appl. Prob. 243–266.CrossRefGoogle Scholar
Miles, R. E. (1984) Sectional Voronoi tessellations. Rev. Mat. Argentina 29, 310–327.Google Scholar
Møller, J. (1989) Random tessellations in d. Adv. Appl. Prob. 21, 37–73.CrossRefGoogle Scholar
Muche, L. (1990) Kontakt- und Sehnenlängenverteilungsfunktionen des Poisson-Voronoi-Mosaiks. Technical Report, Freiberg.Google Scholar
Serra, J. P. (1982) Image Analysis and Mathematical Morphology. Academic Press, London.Google Scholar
Stoyan, D., Kendall, W. S. and Mecke, J. (1987) Stochastic Geometry and Its Application. Wiley, Chichester.CrossRefGoogle Scholar