Research Article
Evaluation of an E-Function when two of the upper Parameters differ by an Integer
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 30-34
-
- Article
-
- You have access
- Export citation
Some Series and Recurrence Relations for MacRobert's E-Function
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 116-117
-
- Article
-
- You have access
- Export citation
Some infinite integrals involving E-functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 183-187
-
- Article
-
- You have access
- Export citation
On a Theorem of Hurwitz
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 90-96
-
- Article
-
- You have access
- Export citation
Summation of a series of products of E-functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 118-120
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 5 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
The Divisibility of Divisor Functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 35-40
-
- Article
-
- You have access
- Export citation
On Riesz summability factors
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 188-196
-
- Article
-
- You have access
- Export citation
An identity in combinatorial analysis
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 197-200
-
- Article
-
- You have access
- Export citation
On the natural representation of the symmetric groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 121-136
-
- Article
-
- You have access
- Export citation
A Class of Irreducible matrix representations of an Arbitrary Inverse Semigroup
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 41-48
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 5 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b6
-
- Article
-
- You have access
- Export citation
Research Article
On a set of normal subgroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 137-146
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 5 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f10
-
- Article
-
- You have access
- Export citation
GMJ volume 5 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 5 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Dual integral equations with trigonometrical kernels†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 147-152
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 5 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 5 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 5 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

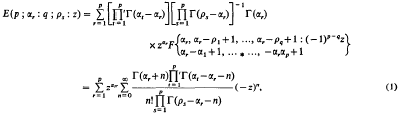

 , a result involving
, a result involving 
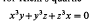
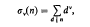
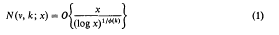
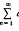 and a number
and a number 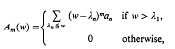
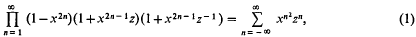
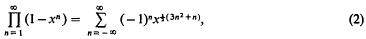
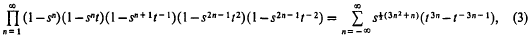
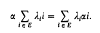
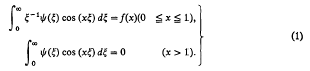
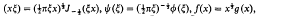 we obtain a pair of dual integral equations of the Titchmarsh type [1, p. 334] with α = − 1,
we obtain a pair of dual integral equations of the Titchmarsh type [1, p. 334] with α = − 1,