We study quantum Schubert varieties from the point of view of regularity conditions. More precisely, we show that these rings are domains that are maximal orders and are AS-Cohen-Macaulay and we determine which of them are AS-Gorenstein. One key fact that enables us to prove these results is that quantum Schubert varieties are quantum graded algebras with a straightening law that have a unique minimal element in the defining poset. We prove a general result showing when such quantum graded algebras are maximal orders. Finally, we exploit these results to show that quantum determinantal rings are maximal orders.

The unit sum number u(R) of a ring R is the least k such that every element is the sum of k units; if there is no such k then u(R) is ω or ∞ depending whether the units generate R additively or not. If RM is a left R-module, then the unit sum number of M is defined to be the unit sum number of the endomorphism ring of M. Here we show that if R is a ring such that R/J(R) is semisimple and is not a factor of R/J(R) and if P is a projective R-module such that JP ≪ P, (JP small in P), then u(P)= 2. As a result we can see that if P is a projective module over a perfect ring then u(P)=2.

This note is devoted to prove some uniqueness results of positive solutions of a Robin problem for semi-linear elliptic equations and systems.

The General Curve Lemma is a tool of Infinite-Dimensional Analysis that enables refined studies of differentiability properties of maps between real locally convex spaces to be made. In this article, we generalize the General Curve Lemma in two ways. First, we remove the condition of local convexity in the real case. Second, we adapt the lemma to the case of curves in topological vector spaces over ultrametric fields.

Let A and B be Hilbert space operators. In this paper we explore the structure of parts of the spectrum of the tensor product A ⊗ B, and conclude some properties that follow from such a structure. We give conditions on A and B ensuring that σw(A ⊗ B) =σw(A)ċσ(B) ∪ σ(A)ċσw(B), where σ(ċ) and σw(ċ) stand for the spectrum and Weyl spectrum, respectively. We also investigate the problem of transferring Weyl and Browder's theorems from A and B to their tensor product A⊗B.

We relate the coefficients of the probabilistic zeta function of a finite monolithic group to those of an almost simple group.

In this paper, some min–max theorems for even and C1 functionals established by Ghoussoub are extended to the case of functionals that are the sum of a locally Lipschitz continuous, even term and a convex, proper, lower semi-continuous, even function. A class of non-smooth functionals admitting an unbounded sequence of critical values is also pointed out.

Let X be a real Banach space, A: X → X a bounded linear operator, and B: X → X a (possibly nonlinear) continuous operator. Assume that λ = 0 is an eigenvalue of A and consider the family of perturbed operators A + ϵB, where ϵ is a real parameter. Denote by S the unit sphere of X and let SA = S ∩ Ker A be the set of unit 0-eigenvectors of A. We say that a vector x0 ∈ SA is a bifurcation point for the unit eigenvectors of A + ϵ B if any neighborhood of (0,0, x0) ∈ 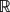× × 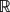X contains a triple (ϵ, λ, x) with ϵ ≠ 0 and x a unit λ-eigenvector of A + ϵB, i.e. x ∈ S and (A + ϵ B)x = λx.

We give necessary as well as sufficient conditions for a unit 0-eigenvector of A to be a bifurcation point for the unit eigenvectors of A + ϵB. These conditions turn out to be particularly meaningful when the perturbing operator B is linear. Moreover, since our sufficient condition is trivially satisfied when Ker A is one-dimensional, we extend a result of the first author, under the additional assumption that B is of class C2.

In this paper, we put forward a cross-constrained variational method to study the non-linear Klein–Gordon equations with an inverse square potential in three space dimensions. By constructing a type of cross-constrained variational problem and establishing so-called cross-invariant manifolds of the evolution flow, we establish some new types of invariant sets for the equation and derive a sharp threshold of blowup and global existence for its solution. Finally, we give an answer to the question how small the initial data are for the global solution to exist.

A maximal symmetry group is a group of isomorphisms of a three-dimensional hyperbolic manifold of maximal order in relation to the volume of the manifold. In this paper we determine all maximal symmetry groups of the types PSL(2, q) and PGL(2, q). Depending on the prime p there are one or two such groups with q=pk and k always equals 1, 2 or 4.

We study the Friedrichs extensions of unbounded cyclic subnormals. The main result of the present paper is the identification of the Friedrichs extensions of certain cyclic subnormals with their closures. This generalizes as well as complements the main result obtained in [5]. Such characterizations lead to abstract Galerkin approximations, generalized wave equations, and bounded -functional calculi.

We construct chaotic m-homogeneous maps acting on for any m ≥ 2, and on the Fréchet spaces for odd values of m ≥ 3 and for any m ≥ 2.

In this paper, we study an upper bound of the fractal dimension of the exponential attractor for the chemotaxis–growth system in a two-dimensional domain. We apply the technique given by Eden, Foias, Nicolaenko and Temam. Our results show that the bound is estimated by polynomial order with respect to the chemotactic coefficient in the equation similar to our preceding papers.

Invariant submanifolds of contact (κ, μ)-manifolds are studied. Our main result is that any invariant submanifold of a non-Sasakian contact (κ, μ)-manifold is always totally geodesic and, conversely, every totally geodesic submanifold of a non-Sasakian contact (κ, μ)-manifold, μ ≠ 0, such that the characteristic vector field is tangent to the submanifold is invariant. Some consequences of these results are then discussed.

In this paper we introduce the notion of normally ordered block-group as a natural extension of the notion of normally ordered inverse semigroup considered previously by the author. We prove that the class NOS of all normally ordered block-groups forms a pseudovariety of semigroups and, by using the Munn representation of a block-group, we deduce the decompositions in Mal'cev products NOS = EIPOI and NOS ∩ A = NPOI, where A, EI and N denote the pseudovarieties of all aperiodic semigroups, all semigroups with just one idempotent and all nilpotent semigroups, respectively, and POI denotes the pseudovariety of semigroups generated by all semigroups of injective order-preserving partial transformations on a finite chain. These relations are obtained after showing the equalities BG = EIEcom = NEcom, where BG and Ecom denote the pseudovarieties of all block-groups and all semigroups with commuting idempotents, respectively.

We make explicit Poincaré duality for the equivariant K-theory of equivariant complex projective spaces. The case of the trivial group provides a new approach to the K-theory orientation [3].

Some oscillation criteria are obtained for the damped PDE with p-Laplacian The results established here are extensions of some classical oscillation theorems due to Fite-Wintner and Kamenev for second order ordinary differential equations, and improve and complement recent results of Mařík and Usami.

We consider a nonlinear Dirichlet problem driven by the p(ċ)-Laplacian. Using variational methods based on the critical point theory, together with suitable truncation techniques and the use of upper-lower solutions and of critical groups, we show that the problem has at least three nontrivial solutions, two of which have constant sign (one positive, the other negative). The hypotheses on the nonlinearity incorporates in our framework of analysis, both coercive and noncoercive problems.

It is well known that a ring R is an exchange ring iff, for any a ∈ R, a−e ∈ (a2−a)R for some e2 = e ∈ R iff, for any a ∈ R, a−e ∈ R(a2−a) for some e2 = e ∈ R. The paper is devoted to a study of the rings R satisfying the condition that for each a ∈ R, a−e ∈ (a2−a)R for a unique e2 = e ∈ R. This condition is not left–right symmetric. The uniquely clean rings discussed in (W. K. Nicholson and Y. Zhou, Rings in which elements are uniquely the sum of an idempotent and a unit, Glasgow Math. J. 46 (2004), 227–236) satisfy this condition. These rings are characterized as the semi-boolean rings with a restricted commutativity for idempotents, where a ring R is semi-boolean iff R/J(R) is boolean and idempotents lift modulo J(R) (or equivalently, R is an exchange ring for which any non-zero idempotent is not the sum of two units). Various basic properties of these rings are developed, and a number of illustrative examples are given.

We consider the equation over a finite field q of q elements, with variables from arbitrary sets . The question of solvability of such and more general equations has recently been considered by Hart and Iosevich, who, in particular, prove that if for some absolute constant C > 0, then above equation has a solution for any λ ∈ q*. Here we show that using bounds of multiplicative character sums allows us to extend the class of sets which satisfy this property.