Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-02T23:43:59.506Z Has data issue: false hasContentIssue false
  • English
  • Français

NORMALIZED EIGENVECTORS OF A PERTURBED LINEAR OPERATOR VIA GENERAL BIFURCATION

Published online by Cambridge University Press:  01 May 2008

RAFFAELE CHIAPPINELLI ,
MASSIMO FURI  and
MARIA PATRIZIA PERA
RAFFAELE CHIAPPINELLI
Affiliation:
Dipartimento di Scienze Matematiche ed Informatiche, Pian dei Mantellini 44, I-53100 Siena, Italy - E-mail address: [email protected]
MASSIMO FURI
Affiliation:
Dipartimento di Matematica Applicata ‘G. Sansone’, Via S. Marta 3, I-50139 Florence, Italy - E-mail address: [email protected]
MARIA PATRIZIA PERA
Affiliation:
Dipartimento di Matematica Applicata ‘G. Sansone‘, Via S. Marta 3, I-50139 Florence, Italy - E-mail address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a real Banach space, A: X → X a bounded linear operator, and B: X → X a (possibly nonlinear) continuous operator. Assume that λ = 0 is an eigenvalue of A and consider the family of perturbed operators A + ϵB, where ϵ is a real parameter. Denote by S the unit sphere of X and let SA = S ∩ Ker A be the set of unit 0-eigenvectors of A. We say that a vector x0 ∈ SA is a bifurcation point for the unit eigenvectors of A + ϵ B if any neighborhood of (0,0, x0) ∈ 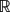× × 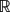X contains a triple (ϵ, λ, x) with ϵ ≠ 0 and x a unit λ-eigenvector of A + ϵB, i.e. x ∈ S and (A + ϵ B)x = λx.

We give necessary as well as sufficient conditions for a unit 0-eigenvector of A to be a bifurcation point for the unit eigenvectors of A + ϵB. These conditions turn out to be particularly meaningful when the perturbing operator B is linear. Moreover, since our sufficient condition is trivially satisfied when Ker A is one-dimensional, we extend a result of the first author, under the additional assumption that B is of class C2.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 50 , Issue 2 , May 2008 , pp. 303 - 318
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Chiappinelli, R.Isolated Connected Eigenvalues in Nonlinear Spectral Theory, Nonlinear Funct. Anal. Appl. 8 (2003), 557–579.Google Scholar
2.Crandall, M. G. and Rabinowitz, P. H.Bifurcation from Simple Eigenvalues, J. Funct. Anal. 8 (1971), 321–340.CrossRefGoogle Scholar
3.Furi, M., Martelli, M. and Pera, M. P., General Bifurcation Theory: Some Local Results and Applications, Differential Equations and Applications to Biology and to Industry (Cooke, K., Cumberbatch, E., Martelli, M., Tang, B. and Thieme, H. Editors), (World Scientific, 1996), 101–115.Google Scholar
4.Furi, M. and Pera, M. P.Co-Bifurcating Branches of Solutions for Nonlinear Eigenvalue Problems in Banach Spaces, Ann. Mat. Pura Appl. 135 (1983), 119–131.CrossRefGoogle Scholar
5.Furi, M. and Pera, M. P.Bifurcation of Fixed Points from a Manifold of Trivial Fixed Points, Nonlinear Funct. Anal. Appl. 11 (2006), 265–292.Google Scholar
6.Hirsch, M. W., Differential Topology, Graduate Texts in Math. 33, (Springer-Verlag, 1976).CrossRefGoogle Scholar
7.Lang, S., Introduction to Differentiable Manifolds, (Interscience Publishers, John Wiley & Sons, Inc., New York, 1966).Google Scholar
8.Martelli, M.Large oscillations of forced nonlinear differential equations, AMS Cont. Mathematics 21 (1983), 151–159.CrossRefGoogle Scholar
9.Nirenberg, L., Topics in Nonlinear Functional Analysis, Courant Institute of Mathematical Sciences, (AMS, New York, 2001).Google Scholar