Research Article
The order problem and the power problem for free product sixth-groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-9
-
- Article
-
- You have access
- Export citation
Primitive sequences whose elements have no large prime factors
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 10-15
-
- Article
-
- You have access
- Export citation
Completely injective semigroups with central idempotents
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 16-20
-
- Article
-
- You have access
- Export citation
Certain congruence and quotient lattices related to completely 0-simple and primitive regular semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 21-24
-
- Article
-
- You have access
- Export citation
On the second natural representation of the symmetric groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 25-37
-
- Article
-
- You have access
- Export citation
On complemented and annihilator algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 38-45
-
- Article
-
- You have access
- Export citation
Decreasing Baer semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 46-51
-
- Article
-
- You have access
- Export citation
Simple proof of a theorem on permanents
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 52-54
-
- Article
-
- You have access
- Export citation
Matrices over orthomodular lattices
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 55-59
-
- Article
-
- You have access
- Export citation
Residuation theory and matrix multiplication on orthomodular lattices
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 60-65
-
- Article
-
- You have access
- Export citation
Remark on a criterion for common transversals
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 66-67
-
- Article
-
- You have access
- Export citation
The numerical range of an element of a normed algebra
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 68-72
-
- Article
-
- You have access
- Export citation
The evaluation functionals associated with an algebra of bounded operators
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 73-76
-
- Article
-
- You have access
- Export citation
Martingale convergence theorems for sequences of Stone algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 77-83
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 10 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 10 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

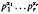 , the
, the 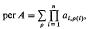
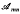 will denote the set of all
will denote the set of all 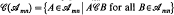 , where we say that
, where we say that 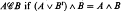 . In § 1 it is shown that mappings from
. In § 1 it is shown that mappings from 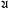 = (
= (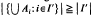
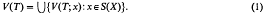
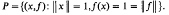
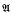 of
of 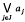 and the greatest lower bound by
and the greatest lower bound by 