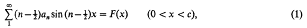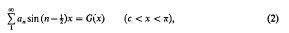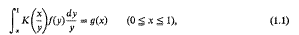Research Article
The translational hull of a completely 0-simple semigroup
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-11
-
- Article
-
- You have access
- Export citation
Translational hull and semigroups of binary relations
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 12-21
-
- Article
-
- You have access
- Export citation
Type Radicals
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 22-29
-
- Article
-
- You have access
- Export citation
Note on a pair of dual trigonometric series
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 30-35
-
- Article
-
- You have access
- Export citation
The torsion of a semi-infinite elastic solid by an elliptical stamp
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 36-45
-
- Article
-
- You have access
- Export citation
Regular ω-semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 46-66
-
- Article
-
- You have access
- Export citation
A procedure for deriving inversion formulae for integral transform pairs of a general kind
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 67-77
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 9 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 9 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation