The Dedekind η-function is defined by

where τ lies in the upper half plane ℋ = {tau;|Im(τ) > 0}, and x = e2πiτ. It is a modular form of weight ½ with a multiplier system. We define an η-product to be a function f (τ) of the form

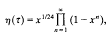
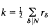where rδ ε ℤ. This is a modular form of weight with a multiplier system. The Fourier coefficients of η-products are related to many well-known number-theoretic functions, including partition functions and quadratic form representation numbers. They also arise from representations of the “monster” group [3] and the Mathieu group M24 [13]. The multiplicative structure of these Fourier coefficients has been extensively studied. Recent papers include [1], [4], [5] and [6]. Here we study the connections between the density of the non-zero Fourier coefficients of f(τ) and the representability of f(τ) as a linear combination of Hecke character forms (defined in Section 4 below). We first make the following definition.

The aim of this paper is to generalise the results of [7] from the prime to the semiprime case. It was shown, for instance, that if M is the annihilator of a simple right module S of projective dimension 1 over a Noetherian prime polynomial identity (PI) ring R then M is either an invertible ideal or an idempotent ideal [7, Proposition 4.2]. One of the main applications of this result was that a prime Noetherian affine PI ring of global dimension less than or equal to 2 is a finite module over its centre. It turns out that this theorem is valid more generally when the ring is semiprime [1, Theorem A]. Clearly this requires [7, Proposition 4.2] also to be strengthened to the semiprime case. We do this by showing that a right invertible maximal ideal in a semiprime Noetherian PI ring is also left invertible (Theorem 3.5).

Bass [1] proved that if R is a left perfect ring, then R contains no infinite sets of orthogonal idempotents and every nonzero left R-module has a maximal submodule, and asked if this property characterizes left perfect rings ([1], Remark (ii), p. 470). The fact that this is true for commutative rings was proved by Hamsher [12], and that this is not true in general was demonstrated by examples of Cozzens [7] and Koifman [14]. Hamsher's result for commutative rings has been extended to some noncommutative rings. Call a ring left duo if every left ideal is two-sided; Chandran [5] proved that Bass’ conjecture is true for left duo rings. Call a ring R weakly left duo if for every r ε R, there exists a natural number n(r) (depending on r) such that the principal left ideal Rrn(r) is two-sided. Recently, Xue [21] proved that Bass’ conjecture is still true for weakly left duo rings.

Brian Hartley asked me whether a free (nilpotent of class 2 and exponent p2)-group of countable rank has a faithful linear representation of finite degree, p here being a prime of course. The answer is yes. The point is that this then yields via work of F. Leinen and M. J. Tomkinson, see [3,3.6] an image of a linear p-group, which is not even finitary linear. The question of which relatively free groups have faithful linear representations dates back at least to work of W. Magnus in the 1930's, see [4, pp. 33, 34 and the final comment on p. 40] for a discussion of this. Our construction, which works more generally, is a further contribution. We write ℜc for the variety of nilpotent groups of class at most c and (ℭ9 for the variety of groups of exponent dividing q.

A kernel functor (equivalently, a left exact torsion preradical) is a left exact subfunctor of the identity on the category R-mod of left R-modules over a ring R with identity. A kernel functor is said to be idempotent if, in addition, σ satisfies σ(M / σ(M)) = 0 for every M ∊ R-mod. To every kernel functor / there corresponds a unique topologizing filter ℒσ = {I Ⅰ σ (R/I) = R/I} of left ideals and a unique class ℱσ = {M ∊ R-mod Ⅰ σ(M) = M} that is closed under homomorphic images, submodules, and direct sums. The idempotence of σ is characterized by either of the following additional conditions:

(1) if I ∊ ℒσ, K ⊆ I, and (K:x) = {r ∊ R ∣ rx ∊ K} ∊ ℒσ for each x ∊ I, then K ∊ ℒ or

(2) ℱσ is closed under extensions of one member of ℱσ by another member of ℱσ Idempotent kernel functors are important since they are the tool used to construct localization functors. For M∊ R-mod, let E(M) denote the injective hull of M. A kernel functor σ is called stable if Mℱ implies that E(M) ∊ ℱσ For more information about kernel functors, see [6], [7], [14], and [15].

The concept of a Hilbert module (over an H*-algebra) arises as a generalization of that of a complex Hilbert space when the complex field is replaced by an (associative) H*-algebra with zero annihilator. P. P. Saworotnow [13] introduced Hilbert modules and extended to its context some classical theorems from the theory of Hilbert spaces, J. F. Smith [17] gave a complete structure theory for Hilbert modules, and G. R. Giellis [9] obtained a nice characteristization of Hilbert modules.

Let R be a commutative ring (with non-zero identity) and let M be an R-module.

We prove that a Banach lattice X is reflexive if and only if X+ does not contain a closed normal cone with an unbounded closed dentable base.

Given a group G and a positive integer k, let vk(G) denote the number of conjugacy classes of subgroups of G which are not subnormal of defect at most k. Groups G such that vkG) < ∝ for some k are considered in Section 2 of [1], and Theorem 2.4 of that paper states that an infinite group G for which vk(G) < ∝ (for some k) is nilpotent provided only that all chief factors of G are locally (soluble or finite). Now it is easy to see that a group G whose chief factors are of this type is locally graded, that is, every nontrivial, finitely generated subgroup F of G has a nontrivial finite image (since there is a chief factor H/K of G such that F is contained in H but not in K). On the other hand, every (locally) free group is locally graded and so there is in general no restriction on the chief factors of such groups. The class of locally graded groups is a suitable class to consider if one wishes to do no more than exclude the occurrence of finitely generated, infinite simple groups and, in particular, Tarski p-groups. As pointed out in [1], Ivanov and Ol'shanskiĭ have constructed (finitely generated) infinite simple groups all of whose proper nontrivial subgroups are conjugate; clearly a group G with this property satisfies v1(G) = l. The purpose of this note is to provide the following generalization of the above-mentioned theorem from [1].

Let M be a smooth m-dimensional submanifold in (m + d)-dimensional Euclidean space ℝm+d For x ∊ M and a non-zero vector X in TXM, we define the (d + l)-dimensional affine subspace E(x, X) ofℝm+d by

Let G be a group and K be a complete ultrametric valued field. Let AP(G, K) be the algebra of the generalized almost periodic functions of G in K. We have shown in a previous paper that when AP(G, K) has an invariant mean, then any almost periodic linear representation is quasi-reducible. Here, we show that with the same hypothesis, any topologically irreducible almost periodic linear representation is finite dimensional; also, any almost periodic linear representation is the topological sum of irreducible representations. Furthermore, we obtain a Peter-Weyl theorem for the algebra AP(G, K).

We use the technical tools of Hopf algebra theory.

This paper shows how to construct Galois field extensions of Hilbertian fields with a given group out of some subclass (called ‘semiabelian groups’ by Matzat [2]) of all soluble groups as Galois group. This is done in a fairly explicit way by constructing polynomials whose Galois groups are universal in the sense that every group in the above subclass is obtained as a quotient of some of them.

In the last few years, there has been considerable interest in the properties of orthogonal polynomials satisfying differential equations (DE) of order greater than two, their connection to singular boundary value problems, their generalizations, and their classification as solutions of second order DE (see for instance [2–8]). In this last interesting problem, some known facts about the classical orthogonal polynomials can be incorporated to connect these two sets of families and yield some nontrivial results in a very simple way. In this paper we only work with the nonclassical Jacobi type, Laguerre type and Legendre type polynomials, and we show how they can be connected with the classical Jacobi, Laguerre and Legendre polynomials, respectively; at the same time we obtain certain bounds for the zeros of the first ones by using a system of nonlinear equations satisfied by the zeros of any polynomial solution of a second order differential equation which, for the classical polynomials is known since Stieltjes and concerns the electrostatic interpretation of the zeros [10, Section 6.7; 9,1]. We also correct an expression for the second order differential equation of the Legendre type polynomials that circulates through the literature.

Group actions on compact surfaces have received considerable attention during the past century. The surface has often carried an analytic structure and been considered a Riemann surface or, equivalently, a complex algebraic curve.