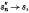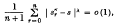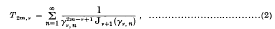Research Article
A generalization of Hurwitz's Theorem
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 101-102
-
- Article
-
- You have access
- Export citation
On Differences of Unitarily Equivalent Self-Adjoint Operators†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 103-107
-
- Article
-
- You have access
- Export citation
The elementary solution of dual integral equations†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 108-110
-
- Article
-
- You have access
- Export citation
Lattice-ordered groups having at most two disjoint elements†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 111-113
-
- Article
-
- You have access
- Export citation
Applications of the multiplication formula for the gamma function to E-function series
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 114-118
-
- Article
-
- You have access
- Export citation
Some recurrence relations and series for the generalised laplace transform
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 119-121
-
- Article
-
- You have access
- Export citation
On Strong and Absolute Summability
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 122-139
-
- Article
-
- You have access
- Export citation
An embedding theorem for groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 140-143
-
- Article
-
- You have access
- Export citation
On some infinite series involving the zeros of Bessel functions of the first kind
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 144-156
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 4 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 4 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

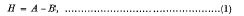
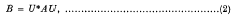
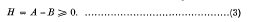
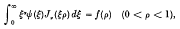
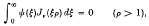
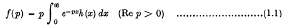
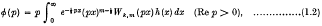
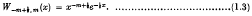
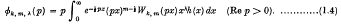
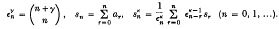
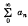 is said to be
is said to be