Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mishra, Babban Prasad
1965.
Some theorems on strong summability.
Mathematische Zeitschrift,
Vol. 90,
Issue. 4,
p.
310.
Borwein, D.
and
Cass, F. P.
1968.
Multiplication theorems for strong N�rlund summability.
Mathematische Zeitschrift,
Vol. 107,
Issue. 1,
p.
33.
Borwein, D.
and
Cass, F. P.
1968.
Strong N�rlund summability.
Mathematische Zeitschrift,
Vol. 103,
Issue. 2,
p.
94.
Cass, Frank P.
1972.
Some Theorems on Strong Nörlund Summability.
Canadian Mathematical Bulletin,
Vol. 15,
Issue. 1,
p.
63.
Heagy, E. C.
and
Shawyer, B. L. R.
1978.
On strong integral summability.
Proceedings of the Edinburgh Mathematical Society,
Vol. 21,
Issue. 1,
p.
73.
Borwein, David
Cass, F. Peter
and
Sayre, John E.
1986.
On absolute generalized Hausdorff summability.
Archiv der Mathematik,
Vol. 46,
Issue. 5,
p.
419.
Borwein, D.
Cass, F. P.
and
Sayre, J. E.
1989.
On strong generalized Hausdorff summability.
Acta Mathematica Hungarica,
Vol. 53,
Issue. 1-2,
p.
95.
Sukla, I.
and
Mohanty, P. C.
1989.
Absolute riesz summability factors.
Periodica Mathematica Hungarica,
Vol. 20,
Issue. 2,
p.
97.
Malkowsky, Eberhard
2021.
Some Compact Operators on the Hahn Space.
Scientific Research Communications,
Vol. 1,
Issue. 1,
p.
1.
Sharma, Kusum
and
Dumka, Diksha
2023.
Convergence of a conjugate function in Zygmund space by almost Nörlund transform.
Journal of Applied Analysis,
Vol. 29,
Issue. 2,
p.
329.


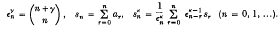
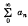 is said to be
is said to be