Research Article
Numerical range estimates for the norms of iterated operators
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 85-87
-
- Article
-
- You have access
- Export citation
On the order of the Sylow subgroups of the automorphism group of a finite group
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 88-96
-
- Article
-
- You have access
- Export citation
The number of irreducible tournaments
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 97-101
-
- Article
-
- You have access
- Export citation
On univalent polynomials
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 102-107
-
- Article
-
- You have access
- Export citation
Note on a partition theorem
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 108-109
-
- Article
-
- You have access
- Export citation
On a theorem of Iseki
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 110-113
-
- Article
-
- You have access
- Export citation
On the dimension of Veblen-Wedderburn systems
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 114-116
-
- Article
-
- You have access
- Export citation
The wave, Laplace, and heat equations and related transforms
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 117-125
-
- Article
-
- You have access
- Export citation
On inequalities for integral operators
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 126-133
-
- Article
-
- You have access
- Export citation
Finitely generated commutative semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 134-151
-
- Article
-
- You have access
- Export citation
A note on Köthe spaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 152-155
-
- Article
-
- You have access
- Export citation
Concerning intrinsic topologies on Boolean algebras and certain bicompactly generated lattices
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 156-161
-
- Article
-
- You have access
- Export citation
Matrix transformations of some sequence spaces—II
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 162-166
-
- Article
-
- You have access
- Export citation
On the natural ordering of
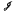 -classes and of idempotents in a regular semigroup
-classes and of idempotents in a regular semigroup
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 167-168
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 11 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 11 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

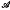 and ℬ, such that every line joining a point in
and ℬ, such that every line joining a point in 
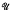 = {
= {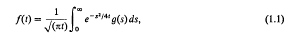

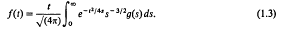
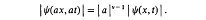
 and if
and if 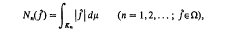
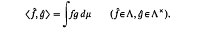
 . The sequence space Γ is a vector space over the complex numbers with seminorms
. The sequence space Γ is a vector space over the complex numbers with seminorms
 -classes and of idempotents in a regular semigroup
-classes and of idempotents in a regular semigroup