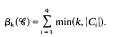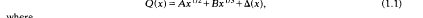Research Article
Rings generated by their regular elements
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-5
-
- Article
-
- You have access
- Export citation
Sums of two regular elements
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 7-11
-
- Article
-
- You have access
- Export citation
On the strongly countable-dimensionality of μ-spaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 13-18
-
- Article
-
- You have access
- Export citation
Subalgebras of C*-algebras and von Neumann algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 19-25
-
- Article
-
- You have access
- Export citation
A note on the invertible ideal theorem
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 27-30
-
- Article
-
- You have access
- Export citation
Addendum to a paper of M. Saks
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 31-33
-
- Article
-
- You have access
- Export citation
A base norm space whose cone is not 1-generating
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 35-36
-
- Article
-
- You have access
- Export citation
Semilocal semigroup rings
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 37-44
-
- Article
-
- You have access
- Export citation
An alternative proof of Diestel's theorem
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 45-46
-
- Article
-
- You have access
- Export citation
On the monodromy groups of lifted Euler equations
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 47-57
-
- Article
-
- You have access
- Export citation
The join of the varieties of strict inverse Semigroups and rectangular bands
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 59-74
-
- Article
-
- You have access
- Export citation
The Galois group of f(xr)
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 75-91
-
- Article
-
- You have access
- Export citation
The motions of algebraic differential equations
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 93-96
-
- Article
-
- You have access
- Export citation
Maximum graphs non-Hamiltonian-connected from a vertex
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 97-98
-
- Article
-
- You have access
- Export citation
A characterization of subnormal operators
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 99-101
-
- Article
-
- You have access
- Export citation
On certain subgroups of a join of subnormal subgroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 103-105
-
- Article
-
- You have access
- Export citation
On Dirichlet series attached to cusp forms and the Siegel-zero
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 107-119
-
- Article
-
- You have access
- Export citation
Averaging operators in non commutative Lp spaces II
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 121-126
-
- Article
-
- You have access
- Export citation
On square-full integers in a short interval
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 127-134
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 25 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f7
-
- Article
-
- You have access
- Export citation

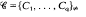 be any partition of
be any partition of