Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-20T17:38:37.846Z Has data issue: false hasContentIssue false
  • English
  • Français

ON IMAGES OF REAL REPRESENTATIONS OF SPECIAL LINEAR GROUPS OVER COMPLETE DISCRETE VALUATION RINGS

Part of: Linear algebraic groups and related topics

Published online by Cambridge University Press:  21 July 2015

TALIA FERNÓS  and
POOJA SINGLA
TALIA FERNÓS
Affiliation:
Department of Mathematics and Statistics, University of North Carolina, Greensboro, North Carolina, USA e-mail: [email protected]
POOJA SINGLA
Affiliation:
Department of Mathematics, Indian Institute of Science, Bangalore 560012, India e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we investigate the abstract homomorphisms of the special linear group SLn($\mathfrak{O}$) over complete discrete valuation rings with finite residue field into the general linear group GLm(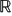$\mathbb{R}$) over the field of real numbers. We show that for m < 2n, every such homomorphism factors through a finite index subgroup of SLn($\mathfrak{O}$). For $\mathfrak{O}$ with positive characteristic, this result holds for all m ∈ 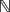${\mathbb N}$.

MSC classification

Primary: 20G25: Linear algebraic groups over local fields and their integers
Secondary: 20G05: Representation theory
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 58 , Issue 1 , January 2016 , pp. 263 - 272
Copyright
Copyright © Glasgow Mathematical Journal Trust 2015 

References

REFERENCES

1.Bass, H., K-theory and stable algebra, Inst. Hautes Études Sci. Publ. Math. 22 (1964), 5–60.CrossRefGoogle Scholar
2.Borel, A. and Chandra, H., Arithmetic subgroups of algebraic groups, Bull. Amer. Math. Soc. 67 (1961), 579–583.CrossRefGoogle Scholar
3.Borel, A. and Chandra, H., Arithmetic subgroups of algebraic groups, Ann. Math. (2) 75 (1962), 485–535.CrossRefGoogle Scholar
4.Borel, A. and Tits, J., Homomorphismes “abstraits“ de groupes algébriques simples, Ann. Math. 97 (1973), 499–571.CrossRefGoogle Scholar
5.Fernós, Talia, Relative property (T) and linear groups, Ann. Inst. Fourier (Grenoble) 56 (6) (2006), 1767–1804.CrossRefGoogle Scholar
6.Humphreys, J. E., Linear algebraic groups (Springer, 1998).Google Scholar
7.Kassabov, M. and Sapir, M. V., Nonlinearity of matrix groups, J. Topol. Anal. 1 (3) (2009), 251–260.CrossRefGoogle Scholar
8.Margulis, G. A., Discrete subgroups of semisimple Lie groups, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) (Results in Mathematics and Related Areas (3)) (Springer-Verlag, Berlin, 1991), volume 17.CrossRefGoogle Scholar
9.Niven, I., Zuckerman, H. S. and Montgomery, H. L., An introduction to the theory of numbers. 5th edition (John Wiley & Sons Inc., New York, 1991).Google Scholar
10.Rapinchuk, I. A., On linear representations of Chevalley groups over commutative rings, Proc. Lond. Math. Soc. (3) 102 (5) (2011), 951–983.CrossRefGoogle Scholar
11.Shenfeld, D. K., On semisimple representations of universal lattices, Groups, Geometry, and Dynamics. 4 (1) (2010), 179–193. http://www.ems-ph.org/journals/show_abstract.php?issn=1661-7207&vol=4&iss=1&rank=8CrossRefGoogle Scholar