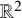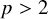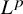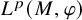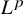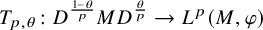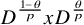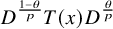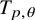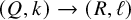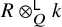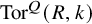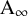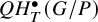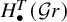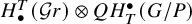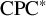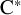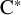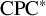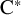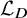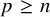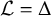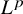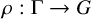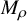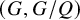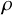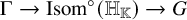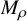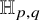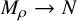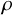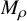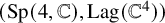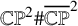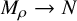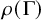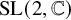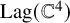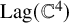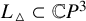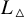Volume 13 - 2025
Mathematical Physics
A mirror theorem for Gromov-Witten theory without convexity
- Part of:
-
- Published online by Cambridge University Press:
- 14 April 2025, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enhanced superconductivity at a corner for the linear BCS equation
- Part of:
-
- Published online by Cambridge University Press:
- 14 April 2025, e71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability
Length spectrum of large genus random metric maps
- Part of:
-
- Published online by Cambridge University Press:
- 10 April 2025, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Canonical integral models for Shimura varieties of abelian type
- Part of:
-
- Published online by Cambridge University Press:
- 07 April 2025, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Equations
Invariant divisors and equivariant line bundles
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2025, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum
Bounding geometrically integral del Pezzo surfaces – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 31 March 2025, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vines and MAT-labeled graphs – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 31 March 2025, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
On the extension of positive maps to Haagerup noncommutative
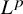 $L^p$-spaces
$L^p$-spaces
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2025, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Koszul homomorphisms and universal resolutions in local algebra
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2025, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Foundations
Tree-like graphings, wallings, and median graphings of equivalence relations
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2025, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Peterson-Lam-Shimozono’s theorem is an affine analogue of quantum Chevalley formula
- Part of:
-
- Published online by Cambridge University Press:
- 24 March 2025, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Deformation theory for prismatic G-displays
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2025, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
k-leaky double Hurwitz descendants
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2025, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
Nuclearity and
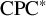 ${\mathrm {CPC}^*}$-Systems
${\mathrm {CPC}^*}$-Systems
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2025, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Equations
Some remarks on Riesz transforms on exterior Lipschitz domains
- Part of:
-
- Published online by Cambridge University Press:
- 19 March 2025, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics
Fiber bundles associated with Anosov representations
- Part of:
-
- Published online by Cambridge University Press:
- 19 March 2025, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology
Relative quantum cohomology of the Chiang Lagrangian
- Part of:
-
- Published online by Cambridge University Press:
- 17 March 2025, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Extremal, enumerative and probabilistic results on ordered hypergraph matchings
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2025, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Deformations of Theta Integrals and A Conjecture of Gross-Zagier
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2025, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Finite Hypergraph Families with Rich Extremal Turán Constructions via Mixing Patterns
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2025, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation