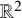Enhanced superconductivity at a corner for the linear BCS equation

Abstract

We consider the critical temperature for superconductivity, defined via the linear BCS equation. We prove that at weak coupling the critical temperature for a sample confined to a quadrant in two dimensions is strictly larger than the one for a half-space, which in turn is strictly larger than the one for $\mathbb {R}^2$. Furthermore, we prove that the relative difference of the critical temperatures vanishes in the weak coupling limit.

1 Introduction

Recent work [18, 19, 1, 2, 21, 20] predicts the occurrence of boundary superconductivity in the BCS model. Close to edges superconductivity sets in at higher temperatures than in the bulk, and at corners the critical temperature appears to be even higher than at edges. A first rigorous justification was provided in [12, 16], where it was proved that the system on half-spaces in dimensions $d\in \{1,2,3\}$ can have higher critical temperatures than on ${\mathbb {R}}^d$ . Here, we consider $d=2$ and the goal is to show that a quadrant has a higher critical temperature than a half-space. Since comparing the critical temperatures for the nonlinear Bardeen–Cooper–Schrieffer model is very difficult, we work with the critical temperature defined via the linear BCS equation and show that a quadrant has a higher critical temperature than a half-space, at least at weak coupling in the same spirit as in [8, 9]. This may serve as a starting point for future investigations of the nonlinear model.

Superconductivity is more stable close to boundaries also when a magnetic field is applied. This phenomenon has been widely studied using Ginzburg–Landau theory; see, for example, [7, 4] and the references therein. Ginzburg–Landau theory can be rigorously derived from BCS theory for domains without boundaries [10, 5, 6], while for domains with boundaries this is an open problem.

We consider the full plane and the half- and quarter-spaces $\Omega _k=(0,\infty )^k \times {\mathbb {R}}^{2-k}$ for $k\in \{0,1,2\}$ . We define the critical temperature as in [12, 16] using the operator

(1.1) $$ \begin{align} H_T^{\Omega}=\frac{-\Delta_x-\Delta_y-2\mu}{\tanh\left(\frac{-\Delta_x-\mu}{2T}\right)+\tanh\left(\frac{-\Delta_y-\mu}{2T}\right)}-\lambda V(x-y) \end{align} $$

acting in $L_{\mathrm {sym}}^2(\Omega \times \Omega )=\{\psi \in L^2(\Omega \times \Omega ) \vert \psi (x,y)=\psi (y,x)\ \mathrm {for\ all}\ x,y\in \Omega \}$ , where $-\Delta $ denotes the Dirichlet or Neumann Laplacian and the subscript indicates on which variable it acts, T is the temperature, $\mu $ is the chemical potential, V is the interaction and $\lambda $ is the coupling constant. The first term is defined through functional calculus. For $V\in L^t({\mathbb {R}}^2)$ with $t>1$ , the $H_T^{\Omega _k}$ are self-adjoint operators defined via the KLMN theorem [16, Remark 2.2].

The critical temperatures are defined as

(1.2) $$ \begin{align} T_c^k(\lambda):= \inf\{T\in (0,\infty) \vert \inf \sigma(H_T^{\Omega_k})\geq 0\}. \end{align} $$

The operator $H_T^{\Omega _k}$ is the Hessian of the BCS functional at the normal state [8], and the linear BCS equation reads $H_T^{\Omega _k} \alpha =0$ .

In particular, the system is superconducting for $T<T_c^k(\lambda )$ , when the normal state is not a minimizer of the full, nonlinear BCS functional. A priori, superconductivity may also occur at temperatures $T>T_c^k(\lambda )$ , either when the ground state energy of the Hessian is not monotone in the temperature or when the normal state is a local minimum of the BCS functional, but not a global one. For translation invariant systems with suitable interactions V, in particular for $\Omega _0={\mathbb {R}}^2$ , this is not the case and the system is in the normal state if $T>T_c^0(\lambda )$ . This was proved in [11, 13] without the restriction to symmetric Cooper pair wave functions and is adapted for symmetric Cooper pair wave functions in [17]. Hence, $T_c^0$ separates the normal and the superconducting phase. However, it remains an open question whether the same is true for $T_c^1$ and $T_c^2$ .

We prove that for small enough $\lambda $ , the critical temperatures defined through the linear criterion (1.2) satisfy $T_c^2(\lambda )>T_c^1(\lambda )$ . Together with the result from [16], we get the strictly decreasing sequence $T_c^2(\lambda )>T_c^1(\lambda )>T_c^0(\lambda )$ of critical temperatures at weak coupling.

Similarly to [16, Lemma 2.3], where it was shown that $T_c^1(\lambda )\geq T_c^0(\lambda )$ for all $\lambda $ , the following Lemma is relatively easy to prove.

Lemma 1.1. Let $\lambda ,T>0$ and $V\in L^{t}({\mathbb {R}}^2)$ for some $t>1$ . Then $\inf \sigma (H_T^{\Omega _2})\leq \inf \sigma (H_T^{\Omega _1})$ .

Its proof can be found in Section 3. In particular, it follows that for all $\lambda>0$ , we have $T_c^2(\lambda )\geq T_c^1(\lambda )$ . The difficulty lies in proving a strict inequality, which the rest of the paper will be devoted to. In order to prove $T_c^2(\lambda )> T_c^1(\lambda )$ , we shall give a precise analysis of the asymptotic behavior of $H_{T_c^1(\lambda )}^{\Omega _1}$ as $\lambda \to 0$ .

For $\mu>0$ let ${\mathcal {F}}:L^1({\mathbb {R}}^2)\to L^2({\mathbb {S}}^{1})$ act as the restriction of the Fourier transform to a sphere of radius $\sqrt \mu $ , that is, ${\mathcal {F}} \psi (\omega )=\widehat \psi (\sqrt {\mu } \omega )$ and for $V\geq 0$ define $O_{\mu }=V^{1/2} {\mathcal {F}}^\dagger {\mathcal {F}} V^{1/2}$ on $L^2({\mathbb {R}}^2)$ . The operator $O_\mu $ is compact. For the desired asymptotic behavior of $H_{T_c^1(\lambda )}^{\Omega _1}$ , we need that $O_\mu $ has a nondegenerate eigenvalue $e_\mu = \sup \sigma (O_\mu )>0$ at the top of its spectrum [13, 14].

We require the following assumptions for our main result.

Assumption 1.2. Let $\mu>0$ . Assume that

1. 1. $V\in L^1({\mathbb {R}}^2) \cap L^{t}({\mathbb {R}}^2)$ for some $t>1$ ,

2. 2. V is radial, $V\not \equiv 0$ ,

3. 3. $\vert \cdot \vert V \in L^1({\mathbb {R}}^2)$ ,

4. 4. $V\geq 0$ ,

5. 5. $e_\mu =\sup \sigma (O_\mu )$ is a nondegenerate eigenvalue.

Remark 1.3. Similarly to the three-dimensional case discussed in [13, Section III.B.1], because of rotation invariance the eigenfunctions of $O_\mu $ are given, in radial coordinates $r \equiv (|r|,\varphi )$ , by $V^{1/2}(r)e^{im\varphi } J_m (\sqrt {\mu }\vert r \vert )$ , where $J_m$ denote the Bessel functions. The corresponding eigenvalues are

(1.3) $$ \begin{align} e_\mu^{(m)}=\frac{1}{2\pi} \int_{{\mathbb{R}}^2} V(r) \vert J_m (\sqrt{\mu}\vert r \vert)\vert^2 {\mathrm{d}} r \end{align} $$

and in particular $e_\mu ^{(m)}=e_\mu ^{(-m)}$ . Assumption (5) therefore means that $e_\mu =e_\mu ^{(0)}$ and that all other eigenvalues $e_\mu ^{(m)}$ are strictly smaller. Hence, the eigenstate corresponding to $e_\mu $ has zero angular momentum. Analogously to the three-dimensional case, a sufficient condition for equation (5) to hold is that $\widehat {V}\geq 0$ .

Our first main result is:

Theorem 1.4. Let $\mu>0$ , and let V satisfy Assumption 1.2. Assume the same boundary conditions, either Dirichlet or Neumann, on $\Omega _1$ and $\Omega _2$ . Then there is a $\lambda _1>0$ , such that for all $0<\lambda <\lambda _1$ , $T_c^2(\lambda )>T_c^1(\lambda )$ .

Remark 1.5. The critical temperature $T_c^1(\lambda )$ is the smallest temperature T satisfying $\inf \sigma (H_{T}^{\Omega _1})=0$ . Other solutions to this equation would define larger critical temperatures. Upon inspection, the proof of Theorem 1.4 shows that for any temperature T satisfying $\inf \sigma (H_{T}^{\Omega _1})=0$ the system on the quadrant is superconducting for temperatures in an interval around T.

The second main result is that the relative difference in critical temperatures vanishes in the weak coupling limit.

Theorem 1.6. Let $\mu>0$ , and let V satisfy Assumption 1.2. Assume either Dirichlet or Neumann boundary conditions on $\Omega _2$ . Then

(1.4) $$ \begin{align} \lim_{\lambda\to0} \frac{T_c^2(\lambda)-T_c^0(\lambda)}{T_c^0(\lambda)}=0. \end{align} $$

Since $T_c^2(\lambda )\geq T_c^1(\lambda )\geq T_c^0(\lambda )$ , this implies $\lim _{\lambda \to 0} \frac {T_c^2(\lambda )-T_c^1(\lambda )}{T_c^1(\lambda )}=0$ and $\lim _{\lambda \to 0} \frac {T_c^1(\lambda )-T_c^0(\lambda )}{T_c^0(\lambda )}=0$ . The latter was already shown in [16], and we closely follow [16] to prove Theorem 1.6.

The paper is structured as follows. In Section 1.1, we explain the proof strategy for Theorem 1.4. Section 3 contains the proofs of some basic properties of $H_T^\Omega $ . Section 4 discusses the regularity and asymptotic behavior of the ground state of $H_T^{\Omega _1}$ . In Section 5, we prove Lemma 1.9, the first key step in the proof of Theorem 1.4. The second key step, Lemma 1.10 is proved in Section 6. In Section 7, we prove Theorem 1.6. Section 8 contains the proofs of auxiliary lemmas.

1.1 Proof strategy for Theorem 2.4

The proof of Theorem 1.4 is based on the variational principle. The idea is to construct a trial state for $H_{T_c^1(\lambda )}^{\Omega _2}$ involving the ground state of $H_{T_c^1(\lambda )}^{\Omega _1}$ . However, the latter operator is translation invariant in the second component of the center of mass variable and therefore has purely essential spectrum. To work with an operator that has eigenvalues, we fix the momentum in the translation invariant direction and choose it in order to minimize the energy.

Let $U:L^2({\mathbb {R}}^2\times {\mathbb {R}}^2)\to L^2({\mathbb {R}}^2\times {\mathbb {R}}^2)$ be the unitary operator switching to relative and center of mass coordinates $r=x-y$ and $z=x+y$ , that is, $U\psi (r,z)= \frac {1}{2}\psi ((r+z)/2,(z-r)/2)$ . We shall apply U to functions defined on a subset of $\Omega \subset {\mathbb {R}}^2\times {\mathbb {R}}^2$ , by identifying $L^2(\Omega )$ with the set of functions in $L^2({\mathbb {R}}^2\times {\mathbb {R}}^2)$ supported in $\Omega $ . The operator $U H_{T}^{\Omega _1} U^\dagger $ , which is $H_T^{\Omega _1}$ transformed to relative and center of mass coordinates, acts on functions on $\tilde \Omega _1 \times {\mathbb {R}}$ , where $\tilde \Omega _1=\{(r,z_1)\in {\mathbb {R}}^{3} \vert \vert r_1\vert < z_1\}$ , and is translation invariant in $z_2$ . For every $q_2\in {\mathbb {R}}$ , let $H_T^1(q_2)$ be the operator obtained from $U H_{T}^{\Omega _1} U^\dagger $ by restricting to momentum $q_2$ in the $z_2$ direction. The operator $H_T^1(q_2)$ acts in $L_{\mathrm {s}}^2(\tilde \Omega _1) =\{\psi \in L^2(\tilde \Omega _1) \vert \psi (r,z_1)=\psi (-r,z_1)\}$ , and we have $\inf \sigma (H_{T_c^1(\lambda )}^{\Omega _1})=\inf _{q_2\in {\mathbb {R}}} \inf \sigma (H_{T_c^1(\lambda )}^1(q_2))$ . We want to choose $q_2$ to be optimal. That this can be done is a consequence of the following Lemma, whose proof will be given in Section 2.2.

Lemma 1.7. Let $T,\lambda , \mu>0$ and $V\in L^t({\mathbb {R}}^2)$ for some $t>1$ . The function $q_2\mapsto \inf \sigma (H_T^1(q_2))$ is continuous, even and diverges to $+\infty $ as $|q_2|\to \infty $ .

Therefore, the infimum is attained and we can define $\eta (\lambda )$ to be the minimal number in $[0,\infty )$ such that $\inf \sigma (H_{T_c^1(\lambda )}^1(\eta (\lambda )))=\inf \sigma (H_{T_c^1(\lambda )}^{\Omega _1})$ .

Next, we shall argue that $H_{T_c^1(\lambda )}^1(\eta (\lambda ))$ indeed has a ground state, at least for small enough coupling, which allows us to construct the desired trial state. By [16, Remark 2.5], there is a $\lambda _1>0$ such that $\inf \sigma (H^{\Omega _0}_{T_c^0(\lambda )})$ is attained at zero total momentum for $\lambda <\lambda _1$ . Let $H_T^0$ denote the operator $H^{\Omega _0}_T$ restricted to zero total momentum. For $\lambda <\lambda _1$ the critical temperature $T_c^0(\lambda )$ is the unique temperature satisfying $\inf \sigma (H_T^0)=0$ . In the weak coupling limit both $T_c^0(\lambda )$ and $T_c^1(\lambda )$ vanish [14], [16, Theorem 1.7]. Furthermore, at weak enough coupling $T_c^1(\lambda )>T_c^0(\lambda )$ [16, Theorem 1.3]. In particular, there is a $\lambda _0>0$ such that for $\lambda \leq \lambda _0$ the critical temperatures satisfy $T_c^0(\lambda )<T_c^1(\lambda )<T_c^0(\lambda _1)$ .

Lemma 1.8. Let $\mu>0$ , let V satisfy Assumption 1.2 and let $0<\lambda \leq \lambda _0$ . Then $H_{T_c^1(\lambda )}^1(\eta (\lambda ))$ has an eigenvalue at the bottom of its spectrum.

The proof of Lemma 1.8 can be found in Section 2.3. For $\lambda \leq \lambda _0$ , let $\tilde \Phi _\lambda $ be the ground state of $H_{T_c^1(\lambda )}^1(\eta (\lambda ))$ . In the case $\eta (\lambda )=0$ , the operator $H_{T_c^1(\lambda )}^1(\eta (\lambda ))$ commutes with reflections $r_2\to -r_2$ and we may assume that $\tilde \Phi _\lambda $ is even or odd under this reflection. Irrespective of the value of $\eta (\lambda )$ , we extend the function $\tilde \Phi _\lambda $ (anti)symmetrically from $\tilde \Omega _1$ to ${\mathbb {R}}^3$ such that the extended function $\Phi _\lambda $ satisfies $\Phi _\lambda ((-r_1,r_2),-z_1)=\Phi _\lambda (r,z_1)$ and $\mp \Phi _\lambda ((z_1,r_2),r_1)=\Phi _\lambda (r,z_1)$ , where $-/+$ corresponds to Dirichlet/Neumann boundary conditions (see Figure 1 for an illustration). The function $\Phi _\lambda $ is the key ingredient for our trial state. Let $\chi _{\tilde \Omega _1}$ denote multiplication by the characteristic function of $\tilde \Omega _1$ ; then $\tilde \Phi _\lambda =\chi _{\tilde \Omega _1} \Phi _\lambda $ . We choose the normalization such that $\lVert V^{1/2}\chi _{\tilde \Omega _1} \Phi _\lambda \rVert _2=1$ , where $V^{1/2}\psi (r,z)=V^{1/2}(r)\psi (r,z)$ . (Since $V\in L^t({\mathbb {R}}^2)$ for some $t>1$ and $\Phi _\lambda \in H^1({\mathbb {R}}^3)$ , it follows by the Hölder and Sobolev inequalities that $V^{1/2} \Phi _\lambda $ is an $L^2$ function [15].)

Figure 1 Sketch of the (anti)symmetric extension of a function $\psi $ defined on the upper right quadrant in the $(r_1,z_1)$ -coordinates. The extension is defined by mirroring along the $x_1$ and $y_1$ -axes and multiplying by $- 1$ for Dirichlet boundary conditions

Our choice of trial state is

(1.5) $$ \begin{align} \psi_\lambda^\epsilon(r_1,r_2,z_1,z_2) &= (\Phi_\lambda(r_1,r_2,z_1) e^{i\eta(\lambda) z_2}+\Phi_\lambda(r_1,-r_2,z_1) e^{-i\eta(\lambda) z_2}) e^{-\epsilon \vert z_2 \vert} \nonumber \\ &\quad \mp(\Phi_\lambda(r_1,z_2,z_1) e^{i\eta(\lambda) r_2}+\Phi_\lambda(r_1,-z_2,z_1) e^{-i\eta(\lambda) r_2}) e^{-\epsilon \vert r_2 \vert} \end{align} $$

for some $\epsilon>0$ . Here and throughout the paper, we use the convention that upper signs correspond to Dirichlet and lower signs to Neumann boundary conditions, unless stated otherwise. The function (1.5) is the natural generalization of the trial state for a half-space used in [16]. Note that $\psi _\lambda ^\epsilon $ is the (anti)symmetrization of $\Phi _\lambda (r,z_1)e^{i \eta (\lambda )z_2-\epsilon |z_2|}$ and satisfies the boundary conditions. The trial state vanishes if $\eta =0$ and $\Phi _\lambda $ is odd under $r_2\to -r_2$ ; our proof will implicitly show that at weak coupling $\Phi _\lambda $ must be even if $\eta =0$ . We shall prove the following two lemmas in Sections 5 and 6, respectively.

Lemma 1.9. Let $\mu>0$ , let V satisfy Assumption 1.2 and let $0<\lambda \leq \lambda _0$ . Then

(1.6) $$ \begin{align} \lim_{\epsilon \to 0} \langle \psi_\lambda^\epsilon, UH^{\Omega_2}_{T_c^1(\lambda)}U^\dagger \psi_\lambda^\epsilon \rangle =\lambda( L_1+L_2) \end{align} $$

with

(1.7) $$ \begin{align} &L_1= \int_{\tilde \Omega_1\times {\mathbb{R}}} \chi_{\vert z_2\vert <\vert r_2\vert}V(r)\bigg(\vert \Phi_\lambda(r_1,r_2,z_1)\vert^2+\vert \Phi_\lambda(r_1,z_2,z_1)\vert^2 \nonumber\\ & \qquad +\overline{\Phi_\lambda(r_1,r_2,z_1)}\Phi_\lambda(r_1,-r_2,z_1)e^{-2i\eta(\lambda) z_2} +\overline{\Phi_\lambda(r_1,z_2,z_1)}\Phi_\lambda(r_1,-z_2,z_1)e^{-2i\eta(\lambda) r_2} \nonumber\\ &\quad \mp \overline{\Phi_\lambda(r_1,r_2,z_1)}\Phi_\lambda(r_1,z_2,z_1)e^{i\eta(\lambda)(r_2- z_2)} \mp \overline{\Phi_\lambda(r_1,z_2,z_1)}\Phi_\lambda(r_1,r_2,z_1)e^{-i\eta(\lambda) (r_2-z_2)} \nonumber\\ & \mp \overline{\Phi_\lambda(r_1,r_2,z_1)}\Phi_\lambda(r_1,-z_2,z_1)e^{-i\eta(\lambda)(r_2+ z_2)} \mp \overline{\Phi_\lambda(r_1,z_2,z_1)}\Phi_\lambda(r_1,-r_2,z_1)e^{i\eta(\lambda) (-r_2+z_2)} \bigg){\mathrm{d}} r {\mathrm{d}} z \end{align} $$

and

(1.8)

where $\widehat \psi (p,q_1)=\int _{{\mathbb {R}}^3} \frac {e^{- i p \cdot r -i q_1 z_1}}{(2\pi )^{3/2}}\psi (r,z_1) {\mathrm {d}} r {\mathrm {d}} z_1 $ denotes the Fourier transform and $\chi _{\tilde \Omega _1}$ denotes multiplication by the characteristic function of $\tilde \Omega _1$ .

Lemma 1.10. Let $\mu>0$ and let V satisfy Assumption 1.2. As $\lambda \to 0$ , we have $L_1=O(1)$ and $L_2\leq - \frac {C}{\lambda }$ for some constant $C>0$ .

In particular, there is a $\lambda _2>0$ such that for all $0<\lambda \leq \lambda _2$ , $\lim _{\epsilon \to 0} \langle \psi _\lambda ^\epsilon , UH^{\Omega _2}_{T_c^1(\lambda )}U^\dagger \psi _\lambda ^\epsilon \rangle <0$ and hence also $\inf \sigma (H^{\Omega _2}_{T_c^1(\lambda )})<0$ . The final ingredient is the continuity of $\inf \sigma (H_T^{\Omega _2}) $ in T, which can be proved analogously to [16, Lemma 4.1]. For $\lambda \leq \lambda _2$ , we have for $T< T_c^1(\lambda )$ by Lemma 1.1 and the definition of $T_c^1$ that $\inf \sigma (H^{\Omega _2}_{T})\leq \inf \sigma (H^{\Omega _1}_{T})< 0$ . We saw that $\inf \sigma (H^{\Omega _2}_{T_c^1(\lambda )})<0$ , and thus by continuity there is an $\epsilon>0$ such that for all $T\in (0,T_c^1(\lambda )+\epsilon ]$ we have $\inf \sigma (H^{\Omega _2}_{T})<0$ . In particular, $T_c^2(\lambda )>T_c^1(\lambda )$ . This concludes the proof of Theorem 1.4.

Remark 1.11. Compared to the proof of $T_c^1(\lambda )>T_c^0(\lambda )$ in [16], there are two main differences and additional difficulties here. The first difference is that $\Phi _\lambda $ here depends on r and $z_1$ and not just r. In particular, we need to understand the dependence and regularity of $\Phi _\lambda $ in $z_1$ . The second difference is that for the full space minimizer it was possible to prove that the optimal momentum in the translation invariant center of mass direction is zero, whereas here we have to work with the momentum $\eta (\lambda )$ , which potentially is nonzero, and we need knowledge about its asymptotics for $\lambda \to 0$ . As a consequence, we may have that $\Phi _\lambda (r_1,r_2,z_1) e^{i\eta (\lambda ) z_2}\neq \Phi _\lambda (r_1,-r_2,z_1) e^{-i\eta (\lambda ) z_2}$ , which is why the expressions in Lemma 1.9 are twice as long as in the analogous ones in [16, Lemma 4.3].

Remark 1.12. The Assumptions 1.2 are almost identical to the assumptions for proving $T_c^1(\lambda )>T_c^0(\lambda )$ in dimension two in [16]. Our method to compute the asymptotics of $\Phi _\lambda $ additionally requires the assumption $V\geq 0$ , however. In particular, in the proof of Lemma 3.2 we require the Birman–Schwinger operators corresponding to $H_T^{\Omega _k}$ to be self-adjoint for technical reasons. No such assumption is needed to determine the asymptotics of the ground state in the translation invariant case; hence, we expect this assumption not to be necessary here either.

Remark 1.13. We expect that our method of proof can also be applied in the three-dimensional case. For a quarter space in $d=3$ , we conjecture that similarly to the case of a half-space [16], the three-dimensional analogues of $L_1$ and $L_2$ in Lemma 1.9 are of equal order and converge to some finite numbers as $\lambda \to 0$ . The limits of $L_1$ and $L_2$ then need to be computed to determine whether $\lim _{\lambda \to 0}(L_1+L_2) <0$ . This makes the computation in three dimensions much more tedious than in two dimensions, which is why we do not work out the details of the three-dimensional case here. Instead, we describe the intuition and the expected outcome. In [16], the ground state on the full space could effectively be replaced by $\Phi _0=(\int _{{\mathbb {R}}^3} V(r) j_3(r)^2{\mathrm {d}} r)^{-1} j_3$ , with $j_3(r)=(2\pi )^{-3/2}\int _{{\mathbb {S}}^2} e^{i \sqrt {\mu } w \cdot r } {\mathrm {d}} \omega $ , in the limit $\lambda \to 0$ . Motivated by the asymptotics of the half-space minimizer $\Phi _\lambda $ in two dimensions proved in Lemma 3.2, we expect that as $\lambda \to 0$ , $\eta (\lambda )\to 0$ and the function $\Phi _\lambda $ behaves like $\Phi _0$ in the r-variable, and concentrates at zero momentum in the $z_1$ direction. A combination of the methods used in [16] and the methods developed in this paper should then allow to compute the limit, and the expected result is

(1.9) $$ \begin{align} \lim_{\lambda\to0} L_1= 2 \int_{{\mathbb{R}}^4} \chi_{|z_2|<|r_2|} V(r) \vert \Phi_0(r)\mp \Phi_0(r_1,z_2,r_3)|^2 {\mathrm{d}} r {\mathrm{d}} z_2 \end{align} $$

and

(1.10) $$ \begin{align} \lim_{\lambda\to0} L_2= -2 \int_{{\mathbb{R}}^4}V(r)| \Phi_0(r_1,z_2,r_3)|^2 {\mathrm{d}} r {\mathrm{d}} z_2 \mp \frac{2\pi}{\mu^{1/2}}\int_{{\mathbb{R}}^3}V(r)|\Phi_0(r)|^2 {\mathrm{d}} r. \end{align} $$

We therefore expect $T_c^2(\lambda )>T_c^1(\lambda )$ at weak enough coupling if V satisfies $\lim _{\lambda \to 0} (L_1+L_2)<0$ , which due to radiality of V and $\Phi _0$ is the same condition as for $T_c^1(\lambda )>T_c^0(\lambda )$ in [16, Theorem 1.3]. In [16, Theorem 1.4 and Remark 1.5] this condition on V is further analyzed.

2 Basic properties of $H_T^{\Omega _1}$ and $H_T^{\Omega _2}$

In this section, we shall introduce some notation that will be useful later on, and prove Lemmas 1.1, 1.7 and 1.8. The following functions will be important to describe the kinetic part of $H_T^\Omega $ :

(2.1) $$ \begin{align} K_T(p,q)=\frac{p^2+q^2-2\mu}{\tanh\left(\frac{p^2-\mu}{2T}\right)+\tanh\left(\frac{q^2-\mu}{2T}\right)},\quad \text{and}\quad B_T(p,q)=\frac{1}{K_T(p+q,p-q)}. \end{align} $$

We may write $B_{T,\mu }$ when the dependence on $\mu $ matters. The function $K_T$ satisfies the following bounds [12, Lemma 2.1].

Lemma 2.1. For every $T>0$ , there are constants $C_1(T,\mu ),C_2(T,\mu )>0$ such that $C_1(1+p^2+q^2)\leq K_{T}(p,q)\leq C_2(1+p^2+q^2)$ .

We will frequently use the following estimates for $B_T$ [16, Eq. (2.3)]:

(2.2) $$ \begin{align} B_T(p,q)\leq \frac{1}{\max\{|p^2+q^2-\mu|,2T\}} \quad \mathrm{and} \quad B_T(p,q)\chi_{p^2+q^2>2\mu>0} \leq \frac{C(\mu)}{1+p^2+q^2}, \end{align} $$

where $C(\mu )$ depends only on $\mu $ .

We use the notation $H^1_0(\Omega )$ for the Sobolev space of functions vanishing at the boundary of $\Omega $ . In the case of Dirichlet boundary conditions, the form domain corresponding to $H_T^{\Omega _k}$ is $D_k^D:=\{\psi \in H^1_0(\Omega _k\times \Omega _k) \vert \psi (x,y)=\psi (y,x)\}$ . For Neumann boundary conditions, one needs to replace the Sobolev space $H^1_0$ by $H^1$ to obtain $D_k^N$ . Let $K_{T}^\Omega $ be the kinetic term in $H_T^\Omega $ . The corresponding quadratic form acts as

(2.3) $$ \begin{align} \langle \psi, K_{T}^\Omega \psi \rangle = \int_{{\mathbb{R}}^{4}}K_{T}(p,q) \left|\int_{\Omega^2}T_\Omega(x,p) T_\Omega(y,q) \psi(x,y) {\mathrm{d}} x {\mathrm{d}} y\right|^2{\mathrm{d}} p{\mathrm{d}} q, \end{align} $$

with

(2.4) $$ \begin{align} T_{\Omega_1}(x,p)=\frac{(e^{-i p_1 x_1}\mp e^{i p_1 x_1}) e^{-i p_2 x_2}}{2^{1/2}2\pi}, \quad \mathrm{and} \quad T_{\Omega_2}(x,p)=\frac{(e^{-i p_1 x_1}\mp e^{i p_1 x_1}) ( e^{-i p_2 x_2}\mp e^{i p_2 x_2})}{4\pi}. \end{align} $$

As already mentioned in the Introduction, we shall use the convention that upper signs correspond to Dirichlet and lower signs to Neumann boundary conditions, unless stated otherwise. We now switch to relative and center of mass coordinates $r=x-y$ , $z=x+y$ , $p'=(p-q)/2$ and $q'=(p+q)/2$ . Note that

(2.5) $$ \begin{align} T_{\Omega_1}(x,p)T_{\Omega_1}(y,p) = \frac{1}{(2\pi)^2}t(p^{\prime}_1,q^{\prime}_1,r_1,z_1)e^{-i ( p_2' r_2+q_2' z_2)}, \end{align} $$

where

(2.6) $$ \begin{align} t(p_1,q_1,r_1,z_1)=\frac{1}{2}\left(e^{-i(p_1 r_1+q_1 z_1)}+e^{i(p_1 r_1+q_1 z_1)}\mp e^{-i(p_1 z_1+q_1 r_1)} \mp e^{i(p_1 z_1+q_1 r_1)}\right). \end{align} $$

Therefore, conjugating the kinetic term $K_T^{\Omega _1}$ with U, which is the operator switching to relative and center of mass coordinates, gives

(2.7) $$ \begin{align} \langle \psi, U K_{T}^{\Omega_1}U^\dagger \psi \rangle = \int_{{\mathbb{R}}^{4}}B_{T}(p',q')^{-1} \left|\int_{\tilde\Omega_1\times {\mathbb{R}}}\frac{1}{(2\pi)^2}t(p^{\prime}_1,q^{\prime}_1,r_1,z_1)e^{-i ( p_2' r_2+q_2' z_2)} \psi(r,z) {\mathrm{d}} r {\mathrm{d}} z\right|^2{\mathrm{d}} p'{\mathrm{d}} q'. \end{align} $$

The operators $H_T^1(q_2)$ defined by restricting $U H_T^{\Omega _1} U^\dagger $ to momentum $q_2$ in $z_2$ -direction can thus be expressed as

(2.8) $$ \begin{align} \langle \psi,H_T^1(q_2) \psi \rangle =\langle \psi, K_T^1(q_2) \psi \rangle-\lambda \int_{\tilde \Omega_1}V(r)\vert \psi(r,z_1)\vert^2 {\mathrm{d}} r{\mathrm{d}} z_1, \end{align} $$

where $\tilde \Omega _1=\{(r,z_1)\in {\mathbb {R}}^{3} \vert \vert r_1\vert < z_1\}$ and the kinetic term $K_T^1(q_2)$ on $L_{\mathrm {s}}^2(\tilde \Omega _1)$ is given by

(2.9) $$ \begin{align} \langle \psi, K_T^1(q_2) \psi \rangle =\int_{{\mathbb{R}}^{3}}B_{T}(p,(q_1,q_2))^{-1} \left|\int_{\tilde\Omega_1}\frac{1}{(2\pi)^{3/2}}t(p_1,q_1,r_1,z_1)e^{-i p_2 r_2} \psi(r,z_1) {\mathrm{d}} r {\mathrm{d}} z_1\right|^2{\mathrm{d}} p{\mathrm{d}} q_1. \end{align} $$

It is convenient to introduce the Birman–Schwinger operators $A_T^0$ and $A_T^1$ corresponding to $H_T^{\Omega _0}$ and $H_T^{\Omega _1}$ , respectively. Let $A_T^0$ be the operator with domain $L^2({\mathbb {R}}^2\times {\mathbb {R}}^2)$ restricted to functions satisfying $\psi (r,z)=\psi (-r,z)$ and given by

(2.10) $$ \begin{align} \langle \psi,A_{T}^0 \psi \rangle=\int_{{\mathbb{R}}^{4}} B_{T}(p,q) |\widehat{ V^{1/2}\psi}(p,q)|^2{\mathrm{d}} p {\mathrm{d}} q. \end{align} $$

Define the operator $A_T^1$ on $\psi \in L_{\mathrm {s}}^2(\tilde \Omega _1 \times {\mathbb {R}})=\{\psi \in L^2(\tilde \Omega _1 \times {\mathbb {R}}) \vert \psi (r,z)=\psi (-r,z)\}$ via

(2.11) $$ \begin{align} \langle \psi, A_{T}^1 \psi \rangle =\int_{{\mathbb{R}}^{4}}B_{T}(p,q) \left|\int_{\tilde\Omega_1\times {\mathbb{R}}}\frac{1}{(2\pi)^2}t(p_1,q_1,r_1,z_1)e^{-i (p_2 r_2+q_2 z_2)} V^{1/2}(r)\psi(r,z) {\mathrm{d}} r {\mathrm{d}} z\right|^2{\mathrm{d}} p{\mathrm{d}} q. \end{align} $$

For $j\in \{0,1\}$ , the operator $A_T^j$ is the Birman–Schwinger operator corresponding to $H_T^{\Omega _j}$ in relative and center of mass variables [16, Section 6]. The Birman–Schwinger principle implies that

$$\begin{align*}\mathrm{sgn} \inf \sigma(H_T^{\Omega_j}) = \mathrm{sgn} (1/\lambda-\sup \sigma(A_T^{j})),\end{align*}$$

where we use the convention that $\mathrm {sgn}\, 0 =0 $ .

Due to translation invariance in $z_2$ , for fixed momentum $q_2$ in this direction, we obtain the operators $A_T^1(q_2)$ on $\psi \in L_{\mathrm {s}}^2(\tilde \Omega _1)$ given by

(2.12) $$ \begin{align} \langle \psi, A_{T}^1(q_2) \psi \rangle =\int_{{\mathbb{R}}^{3}}B_{T}(p,(q_1,q_2)) \left|\int_{\tilde\Omega_1}\frac{1}{(2\pi)^{3/2}}t(p_1,q_1,r_1,z_1) e^{-i p_2 r_2} V^{1/2}(r)\psi(r,z_1) {\mathrm{d}} r {\mathrm{d}} z_1\right|^2{\mathrm{d}} p{\mathrm{d}} q_1. \end{align} $$

The operator $A_T^1(q_2)$ is the Birman–Schwinger version of $H_T^1(q_2)$ . In particular, $H_{T_c^1(\lambda )}^1(\eta (\lambda ))$ has the eigenvalue zero at the bottom of its spectrum if and only if $1/\lambda $ is the largest eigenvalue of $A_{T_c^1(\lambda )}^1(\eta (\lambda ))$ .

Let $\iota : L^2(\tilde \Omega _1)\to L^2({\mathbb {R}}^{3})$ be the isometry

(2.13) $$ \begin{align} \iota \psi(r_1,r_2,z_1) = \frac{1}{\sqrt{2}} (\psi(r_1,r_2,z_1) \chi_{\tilde \Omega_1}(r,z_1) +\psi(-r_1, r_2,-z_1) \chi_{\tilde \Omega_1}(-r_1,r_2,-z_1)). \end{align} $$

Using the definition of t in equation (2.6) and evenness of V in $r_2$ one can rewrite equation (2.12) as

(2.14) $$ \begin{align} \langle \psi, A_{T}^1(q_2) \psi \rangle=\int_{{\mathbb{R}}^3} B_T(p,q)\left \vert \frac{1}{\sqrt{2}}( \widehat{V^{1/2}\iota \psi}(p,q_1)\mp \widehat{ V^{1/2}\iota\psi}((q_1,p_2),p_1)) \right \vert^2 {\mathrm{d}} p {\mathrm{d}} q_1. \end{align} $$

Let $F_2$ denote the Fourier transform in the second variable $F_2 \psi (r, q_1)=\frac {1}{\sqrt {2\pi }} \int _{{\mathbb {R}}} e^{-iq_1 z_1} \psi (r,z_1) {\mathrm {d}} z_1$ and $F_1$ the Fourier transform in the first variable $F_1 \psi (p,q)=\frac {1}{2\pi } \int _{{\mathbb {R}}^2} e^{-ip\cdot r} \psi (r,q) {\mathrm {d}} r.$ Define the operators $G_T(q_2)$ on $L^2({\mathbb {R}}^{3})$ through

(2.15) $$ \begin{align} \langle \psi, G_{T}(q_2) \psi \rangle=\int_{{\mathbb{R}}^{3}} \overline{F_1 V^{1/2}\psi((q_1,p_2),p_1)} B_{T}(p,q) F_1 V^{1/2}\psi(p,q_1) {\mathrm{d}} p {\mathrm{d}} q_1. \end{align} $$

Let $A_{T}^0(q_2) $ acting on $L_{\text {s}}^2({\mathbb {R}}^2\times {\mathbb {R}})$ be given by $\langle \psi ,A_{T}^0(q_2) \psi \rangle =\int _{{\mathbb {R}}^{3}} B_{T}(p,q) |\widehat { V^{1/2}\psi }(p,q_1)|^2{\mathrm {d}} p {\mathrm {d}} q_1$ . It follows from equation (2.14) and $B_T(p,q)=B_T((q_1,p_2),(p_1,q_2))$ that

(2.16) $$ \begin{align} A_T^1(q_2)= \iota^\dagger (A_T^0(q_2)\mp F_2^\dagger G_T(q_2) F_2 ) \iota. \end{align} $$

2.1 Proof of Lemma 1.1

Proof of Lemma 1.1

The goal is to show that $\inf \sigma (H_T^{\Omega _2})\leq \inf \sigma (H_T^{\Omega _1})$ . We proceed analogously to the proof of [16, Lemma 2.3]. Let $S_l$ be the shift by l in the second component, that is, $S_l \psi (x,y)= \psi ((x_1, x_2-l), (y_1,y_2-l))$ . Let $\psi $ be a function in $D_1^{D/N}$ with bounded support, for the case of Dirichlet/Neumann boundary conditions, respectively. For l big enough, $S_l \psi $ is supported on $\Omega _2\times \Omega _2$ and satisfies the boundary conditions. The goal is to prove that $\lim _{l\to \infty } \langle S_l \psi , H^{\Omega _2}_T S_l \psi \rangle = \langle \psi , H^{\Omega _1}_T \psi \rangle $ . Then, since functions with bounded support are dense in $D_1^{D/N}$ (with respect to the Sobolev norm), the claim follows.

Note that $\langle S_l \psi ,V S_l \psi \rangle = \langle \psi ,V \psi \rangle $ . Let $\tilde \psi $ be the (anti-)symmetric continuation of $\psi $ from $\Omega _1\times \Omega _1$ to ${\mathbb {R}}^2\times {\mathbb {R}}^2$ as in Figure 1, giving $\tilde \psi \in H^1({\mathbb {R}}^4)$ . Furthermore, using symmetry of $K_T$ in $p_2$ and $q_2$ one obtains

(2.17) $$ \begin{align} \langle S_l \psi,K_T^{\Omega_2} S_l \psi \rangle &=\frac{1}{4}\int_{{\mathbb{R}}^{4}}\overline{\widehat{ \tilde \psi}(p,q)}K_T(p,q) \Big[\widehat{ \tilde \psi}(p,q)\mp\widehat{ \tilde \psi}((p_1,-p_2),q) e^{i 2l p_2}\mp \widehat{ \tilde \psi}(p,(q_1,-q_2))e^{i 2l q_2} \nonumber\\ &\quad +\widehat{ \tilde \psi}((p_1,- p_2),(q_1,-q_2))e^{i 2l (p_2+q_2)}\Big] {\mathrm{d}} p{\mathrm{d}} q \end{align} $$

for l big enough such that $S_l \psi $ is supported on $\Omega _2\times \Omega _2$ . The first term is exactly $\langle \psi ,K_T^{\Omega _1} \psi \rangle $ . Note that by the Schwarz inequality and since $K_T(p,q)\leq C(1+p^2+q^2)$ according to Lemma 2.1, the function

(2.18) $$ \begin{align} (p,q)\mapsto \overline{\widehat{ \tilde \psi}(p,q)}K_T(p,q)\widehat{ \tilde \psi}((p_1,-p_2),q) \end{align} $$

is in $L^1({\mathbb {R}}^{2d})$ since $\tilde \psi \in H^1({\mathbb {R}}^{4})$ . By the Riemann–Lebesgue lemma, the second term in equation (2.17) vanishes for $l\to \infty $ . By the same argument, also the remaining terms vanish in the limit.

2.2 Proof of Lemma 1.7

Proof of Lemma 1.7

To prove continuity of the function $q_2\mapsto \inf \sigma (H_T^1(q_2))$ , it suffices to show that for all $T>0$ and $\mu ,Q_0,Q_1\in {\mathbb {R}}$ there is a constant $C(T,\mu ,Q_0,Q_1)$ such that for all $Q_0<q_2,q_2'<Q_1$ we have

$$\begin{align*}|B_T(p,q)^{-1}-B_T(p,(q_1,q_2'))^{-1}| \leq C(T,\mu,Q_0,Q_1) |q_2-q_2'|(1+p^2+q_1^2). \end{align*}$$

The claim then follows analogously to the proof of [16, Lemma 4.1].

We write

$$\begin{align*}B_T(p,q)^{-1}-B_T(p,(q_1,q_2'))^{-1}=(q_2'-q_2)f(p,q,q_2'-q_2) B_T^{-1}(p,(q_1,q_2')) B_T^{-1}(p,q), \end{align*}$$

where f is defined as in the following lemma.

Lemma 2.2. Let $T,\mu ,Q_1>0$ and define the function $f:{\mathbb {R}}^2\times {\mathbb {R}}^2 \times {\mathbb {R}}\to {\mathbb {R}}$ through

(2.19) $$ \begin{align} f(p,q,x)=\frac{1}{x}\left(B_T(p,(q_1,q_2+x))-B_T(p,q)\right) \end{align} $$

for $x\neq 0$ and $f(p,q,0)=\partial _{q_2} B_T(p,q)$ . Then f is continuous and for $|q_2|<Q_1$ there is a constant C depending only on $T, \mu $ and $Q_1$ such that

(2.20) $$ \begin{align} |f(p,q,x)|\leq \frac{C}{1+p_1^2+p_2^2+q_1^2}. \end{align} $$

The proof is provided in Section 7.1. Together with $B_T^{-1}(p,q)\leq C(1+p^2+q^2)$ (c.f Lemma 2.1) the desired bound on $|B_T(p,q)^{-1}-B_T(p,(q_1,q_2'))^{-1}|$ follows.

The function $q_2\to \inf \sigma (H_T^1(q_2))$ is even since $\langle \psi , H_T^1(-q_2) \psi \rangle = \langle \tilde \psi , H_T^1(q_2) \tilde \psi \rangle $ , where $\tilde \psi (r,z_1)=\psi ((r_1,-r_2),z_1)$ , which follows directly from the definitions of $H_T^1(q_2)$ and $K_T(q_2)$ in equations (2.8) and (2.9) using radiality of V and substituting $(p_2,r_2)\to -(p_2,r_2)$ . The divergence of $\inf \sigma (H_T^1(q_2))$ as $|q_2|\to \infty $ follows since the function $B_T(p,q)^{-1}$ in $K_T(q_2)$ is bounded below by $|p^2+q^2-\mu |$ ; see equation (2.2).

2.3 Proof of Lemma 1.8

Proof of Lemma 1.8

The half-space Birman–Schwinger operator $A_{T}^1(q_2)$ for $q_2\in {\mathbb {R}}$ can be decomposed into a term involving $A_T^0(q_2)$ and a perturbation involving $G_T(q_2)$ according to equation (2.16). The operator $A_T^0(q_2)$ has purely essential spectrum and let $a_T^0:=\sup \sigma (A_T^0)$ .

Below, we shall prove that $G_T(q_2)$ is compact. The part of the spectrum of $A_T^1$ that lies above $a_T^0$ hence consists of eigenvalues.

We first argue that $A_{T_c^1(\lambda )}^1$ has spectrum above $a_{T_c^1(\lambda )}^0$ . The Birman–Schwinger principle implies

$$\begin{align*}\sup \sigma(A_{T_c^1(\lambda)}^1(\eta(\lambda)))=\lambda^{-1}=a_{T_c^0(\lambda)}^0. \end{align*}$$

We need to show that $a_{T_c^0(\lambda )}^0>a_{T_c^1(\lambda )}^0$ . The idea is to use that $a_T^0$ is strictly decreasing in T when the supremum of $\sigma (A_T^0)$ is attained at zero total momentum and that $T_c^1(\lambda )>T_c^0(\lambda )$ at weak coupling. At weak coupling $\lambda <\lambda _1$ , $\inf \sigma (H_{T_c^0(\lambda )}^{\Omega _0})$ is attained at zero total momentum and $T_c^0$ is uniquely determined by $\inf \sigma (H^0_{T_c^0(\lambda )})=0$ . The Birman–Schwinger principle implies that the supremum of $\sigma (A_T^0)$ is attained at zero total momentum, that is, $a_T^0=\sup \sigma (A_T^0(0))$ for $T< T_c^0(\lambda _1)$ . At weak enough coupling $\lambda \leq \lambda _0$ , we have $T_c^0(\lambda _1)>T_c^1(\lambda )>T_c^0(\lambda )$ . Using the strict monotonicity of $a_T^0$

$$\begin{align*}\sup \sigma(A_{T_c^1(\lambda)}^1(\eta(\lambda)))=a_{T_c^0(\lambda)}^0> a_{T_c^1(\lambda)}^0. \end{align*}$$

Hence, $\lambda ^{-1}$ is an eigenvalue of $A_{T_c^1(\lambda )}^1(\eta (\lambda ))$ and by the Birman–Schwinger principle $H_{T_c^1(\lambda )}^1(\eta (\lambda ))$ has an eigenvalue at the bottom of the spectrum.

To prove compactness of $G_T(q_2)$ defined in equation (2.15), we prove that its Hilbert–Schmidt norm is finite. Writing out the Hilbert–Schmidt norm in terms of the integral kernel of $G_T(q_2)$ and carrying out the integrations over relative and center of mass coordinates, one obtains

(2.21) $$ \begin{align} \lVert G_T(q_2)\rVert_{\mathrm{HS}}^2 = \int_{{\mathbb{R}}^4} \vert \widehat{V}(0,p_2-p_2')\vert^2 B_T(p,q)B_T((p_1,p_2'),q) {\mathrm{d}} p_1 {\mathrm{d}} q_1 {\mathrm{d}} p_2 {\mathrm{d}} p_2'. \end{align} $$

Using $B_T(p,q)\leq C(T,\mu )/(1+p^2+q^2)$ (c.f. equation (2.2)) and Young’s inequality, this is bounded above by

(2.22) $$ \begin{align} C(T,\mu)^2 \left(\int_{\mathbb{R}} \vert \widehat{V}(0,\vert p_2 \vert)\vert^{2r}{\mathrm{d}} p_2 \right)^{1/r} \int_{{\mathbb{R}}}\left(\int_{{\mathbb{R}}} \left(\frac{1}{1+p_1^2+q_1^2+p_2^2}\right)^s {\mathrm{d}} p_2 \right)^{2/s}{\mathrm{d}} p_1 {\mathrm{d}} q_1, \end{align} $$

where $2=1/r+2/s$ . By assumption, $V\in L^1\cap L^t$ for some $t>1$ . Note that $\widehat {V}$ is continuous by Riemann–Lebesgue and $\widehat {V}\in L^{t'} \cap L^\infty $ for some $t'<\infty $ by the Hausdorff–Young inequality. In particular, due to the radiality of V, we can bound $\left (\int _{\mathbb {R}} \vert \widehat {V}(0,\vert p_2 \vert ) \vert ^{2r}\right )^{1/r}\leq \lVert V\rVert _\infty ^2+\frac {1}{2\pi }\lVert \widehat {V}\rVert _{2r}^2$ , which is finite for the choice $r=t'/2$ . With this choice, we have $s>1$ . Note that $ \left (\int _{{\mathbb {R}}}\left (\frac {1}{1+p_1^2+q_1^2+p_2^2}\right )^s {\mathrm {d}} p_2 \right )^{2/s} =\frac {C}{(1+p_1^2+q_1^2)^{2-1/s}}$ for some constant C. Hence, the integral over $p_1,q_1$ in equation (2.22) is finite for $s>1$ .

3 Regularity and asymptotic behavior of the half-space ground state

In this section, we collect regularity and convergence results for $\Phi _\lambda $ (defined in Section 1.1), which we shall use later to prove Lemmas 1.9 and 1.10. The asymptotics of $T_c^0(\lambda )$ and $T_c^1(\lambda )$ for $\lambda \to 0$ are known:

Remark 3.1. At weak enough coupling, $\inf \sigma (H_{T_c^0(\lambda )}^{\Omega _0})$ is attained at zero total momentum [16, Remark 2.5]. In the case of zero total momentum, the asymptotics of $T_c^0(\lambda )$ were computed in [14, Theorem 2.5] to be $\vert \lambda ^{-1}- e_\mu \ln \frac {\mu }{T_c^0(\lambda )}\vert =O(1)$ for $\lambda \to 0$ . Furthermore, [16, Theorem 1.7] implies that $\ln \frac {\mu }{T_c^0(\lambda )}-\ln \frac {\mu }{T_c^1(\lambda )}=o(1)$ for $\lambda \to 0$ . Therefore, $\vert \lambda ^{-1}- e_\mu \ln \frac {\mu }{T_c^1(\lambda )}\vert =O(1)$ as well. In particular, both $T_c^0(\lambda )$ and $T_c^1(\lambda )\to 0$ as $ \lambda \to 0$ exponentially fast.

Let $\Psi _\lambda (r,z_1):=\frac {1}{\sqrt {2}} V^{1/2}(r) \Phi _\lambda (r,z_1) \chi _{|r_1|<|z_1|}$ as function on ${\mathbb {R}}^3$ . Note that $\lVert \Psi _\lambda \rVert _2=1$ due to the symmetry under $(r_1,z_1)\to -(r_1,z_1)$ and the normalization $\lVert V^{1/2}\chi _{\tilde \Omega _1} \Phi _\lambda \rVert _2=1$ . The first convergence result describes the asymptotic behavior of $\eta (\lambda )$ and $\Psi _\lambda $ as $\lambda \to 0$ . According to the Birman–Schwinger principle, $\chi _{\tilde \Omega _1}\Psi _\lambda $ is an eigenvector of $A_{T_c^1(\lambda )}(\eta (\lambda ))$ corresponding to the largest eigenvalue.

Let

(3.1) $$ \begin{align} j_2(r):=\frac{1}{2\pi}\int_{{\mathbb{S}}^{1}} e^{i \omega \cdot r \sqrt{\mu}} {\mathrm{d}} \omega. \end{align} $$

Due to assumptions 1.2(2) and (5), the eigenvector corresponding to the largest eigenvalue $e_\mu $ of $O_\mu $ has angular momentum zero and is given by [16]

(3.2) $$ \begin{align} \psi^0(r)=\frac{V^{1/2}(r)j_2(r)}{\Big(\int_{{\mathbb{R}}^2}V(r')j_2(r')^2 {\mathrm{d}} r'\Big)^{1/2}}. \end{align} $$

Let ${\mathbb {P}}:L^2({\mathbb {R}}^3)\to L^2({\mathbb {R}}^3)$ denote the projection onto $\psi ^0$ in the r-variable, that is,

$$\begin{align*}{\mathbb{P}} \psi (r,q_1)= \psi^0(r) \int_{{\mathbb{R}}^2} \overline{\psi^0(r')} \psi(r',q_1) {\mathrm{d}} r'.\end{align*}$$

For $0\leq \beta <1$ let ${\mathbb {Q}}_\beta $ denote the projection onto small momenta in $q_1$ , that is,

$$\begin{align*}{\mathbb{Q}}_\beta \psi (r,q_1)=\psi (r,q_1) \chi_{\frac{\vert q_1\vert}{\sqrt{\mu}}<\left(\frac{T_c^1(\lambda)}{\mu}\right)^\beta}.\end{align*}$$

Let ${\mathbb {P}}^\perp ={\mathbb {I}}-{\mathbb {P}}$ and ${\mathbb {Q}}_\beta ^\perp =1-{\mathbb {Q}}_\beta $ .

Our first convergence result for the minimizer of $H_{T_c^1(\lambda )}^{\Omega _1}$ is that for $\lambda \to 0$ the optimal momentum $\eta (\lambda )\to 0$ and $\Psi _\lambda $ concentrates at momentum zero in $z_1$ direction and approaches $\psi ^0$ in the r-variables. This is made precise in the following Lemma, whose proof can be found in Section 3.1.

Lemma 3.2. Let $\mu>0$ , V satisfy Assumption 1.2, and let $0\leq \beta < 1$ . For $\lambda \to 0$ , we have

1. 1. $\eta (\lambda )=O(T_c^1(\lambda ))$

2. 2. $\lVert {\mathbb {P}}^\perp F_2 \Psi _\lambda \rVert _2^2 =O(\lambda )$

3. 3. $\lVert {\mathbb {Q}}_\beta ^\perp F_2 \Psi _\lambda \rVert _2^2 =O(\lambda )$ .

For a function f depending on two variables, we define the mixed Lebesgue norm $\lVert f \rVert _{L_i^p L_j^q}$ for $\{i,j\}=\{1,2\}$ , as first taking the $L^q$ -norm in the j-th variable and then taking the $L^p$ -norm in the i-th variable. The following estimate is analogous to [16, Lemma 3.7] and follows from the Cauchy-Schwarz inequality.

Lemma 3.3. Let $V\in L^1({\mathbb {R}}^2)$ and $\psi \in L^2({\mathbb {R}}^2\times {\mathbb {R}})$ . Then

(3.3) $$ \begin{align} \lVert \widehat{V^{1/2}\psi} \rVert_{L_1^\infty L_{2}^2} & \leq \sup_p \left( \int_{\mathbb{R}} \vert \widehat{V^{1/2}\psi}(p,q_1)\vert^2 {\mathrm{d}} q_1\right)^{1/2} \nonumber\\ & \leq \lVert \widehat{V^{1/2}\psi} \rVert_{ L_2^2 L_1^\infty}=\left(\int_{\mathbb{R}}\sup_p \vert \widehat{V^{1/2}\psi}(p,q_1)\vert^2 {\mathrm{d}} q_1\right)^{1/2} \leq \frac{\lVert V\rVert_1^{1/2}}{2\pi} \lVert \psi\rVert_2. \end{align} $$

To simplify notation, we shall sometimes write $T_c^1,\eta $ instead of $T_c^1(\lambda ),\eta (\lambda )$ . Recall the definition of $t(p_1,q_1,r_1,z_1)$ from equation (2.6) and note that due to the (anti-)symmetry of $\Phi _\lambda $

(3.4) $$ \begin{align} \frac{1}{(2\pi)^{3/2}}\int_{\tilde \Omega_1} t(p_1,q_1,r_1,z_1)e^{-i p_2 r_2}\Phi_\lambda(r,z_1){\mathrm{d}} r {\mathrm{d}} z_1= \frac{1}{2}\widehat{\Phi_\lambda}(p,q_1). \end{align} $$

Combining this with the eigenvalue equation $\chi _{\tilde \Omega _1} \Phi _\lambda =\lambda (K_{T_c^1(\lambda )}^1(\eta (\lambda ))^{-1} V \chi _{\tilde \Omega _1} \Phi _\lambda $ gives

(3.5) $$ \begin{align} \widehat{\Phi_\lambda}(p,q_1) =\frac {2\lambda} {(2\pi)^{3/2}} \int_{\tilde \Omega_1}B_{T_c^1(\lambda)}(p,(q_1,\eta(\lambda))) \ t(p_1,q_1,r^{\prime}_1,z_1')e^{-i p_2 r^{\prime}_2} V(r') \Phi_\lambda(r',z_1') {\mathrm{d}} r' {\mathrm{d}} z_1' \end{align} $$

for $(p,q_1)\in {\mathbb {R}}^3$ .

To describe the asymptotics of $\Phi _\lambda $ for $\lambda \to 0$ , it is convenient to split the function into different summands with different asymptotic properties. We use equation (3.5) together with $\Psi _\lambda =\frac {1}{\sqrt {2}} V^{1/2}\Phi _\lambda \chi _{|r_1|<|z_1|}$ to split $\Phi _\lambda $ into the sum $\Phi _\lambda ^{d}\mp \Phi _\lambda ^{ex}$ , where the first term uses the first two summands of $t(p_1,q_1,r^{\prime }_1,z^{\prime }_1)$

(3.6) $$ \begin{align} \Phi_\lambda^{d}(r,z_1)=\sqrt{2}\lambda\int_{{\mathbb{R}}^{3}} \frac{e^{i (p\cdot r +q_1 z_1)}}{(2\pi)^{3/2}} B_{T_c^1}(p,(q_1,\eta)) \widehat{V^{1/2}\Psi_\lambda}(p, q_1){\mathrm{d}} p{\mathrm{d}} q_1, \end{align} $$

and the second term uses the last two summands of $t(p_1,q_1,r^{\prime }_1,z^{\prime }_1)$

(3.7) $$ \begin{align} \Phi_\lambda^{ex}(r,z_1)=\sqrt{2} \lambda\int_{{\mathbb{R}}^{3}}\frac{e^{i (p\cdot r +q_1 z_1)}}{(2\pi)^{3/2}} B_{T_c^1}(p,(q_1,\eta)) \widehat{V^{1/2}\Psi_\lambda}(( q_1,p_2), p_1){\mathrm{d}} p{\mathrm{d}} q_1. \end{align} $$

For $j\in \{d,ex\}$ , we further split $\Phi ^{j}_\lambda =\Phi ^{{j},<}_\lambda +\Phi ^{{j},>}_\lambda $ , where $\Phi ^{{j},\#}$ for $\#\in \{<,>\}$ has the characteristic function $\chi _{p^2+q_1^2\#2\mu }$ in the integrand. Furthermore, let $\Phi ^{\#}=\Phi ^{d,\#}\mp \Phi ^{ex,\#}$ .

The following three lemmas contain regularity properties for $\Phi _\lambda $ , which are later used for dominated convergence arguments in the proof of Lemma 1.9. Furthermore, they also contain information about the weak coupling behavior of the different $\Phi _\lambda ^{j,\#}$ , which is important for the proof of Lemma 1.10. The first lemma is useful to prove that $L_1$ is of order $O(1)$ .

Lemma 3.4. Let $\mu>0$ , let V satisfy Assumption 1.2 and let $0<\lambda \leq \lambda _0$ . Then $ \lVert \Phi _\lambda \rVert _{L_1^\infty L_{2}^2} <\infty. $ Furthermore, $\lVert \Phi _\lambda ^d \rVert _{L_1^\infty L_{2}^2}=O(1)$ and $\lVert \Phi _{\lambda }^{ex,>}\rVert _{L_1^\infty L_{2}^2}=O(\lambda )$ as $\lambda \to 0$ .

To understand the asymptotics of $L_2$ the following result comes in handy.

Lemma 3.5. Let $\mu>0$ , let V satisfy Assumption 1.2 and let $0<\lambda \leq \lambda _0$ . The function $(r,z)\mapsto V^{1/2}(r) \vert \Phi _\lambda (r_1,z_2,z_1)\vert $ is in $L^2({\mathbb {R}}^4)$ . Furthermore, as $\lambda \to 0$ , the $L^2({\mathbb {R}}^4)$ -norms of the functions $V^{1/2}(r) \vert \Phi _\lambda ^{>}(r_1,z_2,z_1)\vert $ , $V^{1/2}(r) \vert \Phi _\lambda ^{d,<}(r_1,z_2,z_1)\vert $ and $V^{1/2}(r) \vert \Phi _\lambda ^{ex,<}(r_1,z_2,z_1)\vert $ are of order $O(\lambda )$ , $O(\lambda ^{-1/2})$ , and $O(\lambda ^{1/2})$ , respectively.

This suggests that the only possible origin for divergence in $L_2$ lies in contributions from $V^{1/2}(r) \vert \Phi _\lambda ^{d,<}(r_1,z_2,z_1)|$ . In the proof of Lemma 1.10, we shall show that the $L^2$ norm of this term indeed grows as $\lambda ^{-1/2}$ , resulting in the $1/\lambda $ divergence of $L_2$ . Furthermore, we need the following for the proof of Lemma 1.9.

Lemma 3.6. Let $\mu>0$ , let V satisfy Assumption 1.2 and let $0<\lambda \leq \lambda _0$ . Define the functions $g_0$ , $g_+$ and $g_{-}$ on ${\mathbb {R}}^2$ as

(3.8)

and

(3.9) $$ \begin{align} g_\pm (p_2,q_2):=\int_{{\mathbb{R}}^2}\overline{\widehat \Phi_\lambda(p,q_1) } \Big[B_{T_c^1}^{-1}(p,q) -B_{T_c^1}^{-1}(p,(q_1,\eta)) \Big] \widehat \Phi_\lambda((p_1,\pm q_2),q_1) {\mathrm{d}} p_1 {\mathrm{d}} q_1. \end{align} $$

The functions $g_0$ and $g_\pm $ are continuous and bounded and $g_\pm (p_2,\eta )=0$ for all $p_2 \in {\mathbb {R}}$ .

The proofs of these three lemmas are given in Sections 4.2 – 4.4, which may be skipped at first reading.

3.1 Proof of Lemma 3.2

Proof of Lemma 3.2

Recall the operators $ A_T^0$ , and $A_T^1$ from Section 3, and let $a_T^j=\sup \sigma (A_T^j)$ . In the proof of [16, Theorem 1.7] it was shown that $a_T^0\leq a_T^1$ for all $T>0$ . Recall the decomposition of $A_T^1(q_2)$ into $A_T^0(q_2)$ and $G_T(q_2)$ in (2.16). The operator norm of $G_T(q_2)$ is bounded uniformly in T and $q_2$ according to [16, Lemma 6.1]. Recall that $\sqrt {2}\chi _{\tilde \Omega _1} \Psi _\lambda $ is a normalized eigenvector of $A^1_{T_c^1(\lambda )}(\eta (\lambda ))$ , and note that $\iota \sqrt {2}\chi _{\tilde \Omega _1} \Psi _\lambda =\Psi _\lambda $ , where $\iota $ is the isometry extending a function defined on $\tilde \Omega _1$ to ${\mathbb {R}}^3$ symmetrically under $(r_1,z_1)\to -(r_1,z_1)$ ; see equation (2.13). With the asymptotics $T_c^1(\lambda )\to 0$ for $\lambda \to 0$ and $a_T^0=e_\mu \ln (\mu /T)+O(1)$ for $T\to 0 $ discussed in Remark 3.1, we have for $\lambda \to 0$

(3.10) $$ \begin{align} e_\mu \ln \mu/T_c^1(\lambda)+O(1)= a_{T_c^1(\lambda)}^0 \leq a_{T_c^1(\lambda)}^1 = \langle \Psi_\lambda, A_{T_c^1(\lambda)}^0(\eta(\lambda )) \Psi_\lambda \rangle +O(1). \end{align} $$

For $q\in {\mathbb {R}}^2$ , let $B_{T}(\cdot ,q)$ denote the operator on $L^2({\mathbb {R}}^2)$ which acts as multiplication by $B_{T}(p,q)$ (defined in equation (2.1)) in momentum space. Note that

(3.11) $$ \begin{align} \langle \Psi_\lambda, A_{T_c^1(\lambda)}^0(\eta(\lambda )) \Psi_\lambda \rangle = \int_{\mathbb{R}} \langle F_2 \Psi_\lambda(\cdot , q_1) , V^{1/2}B_{T_c^1(\lambda)}(\cdot, (q_1,\eta(\lambda))) V^{1/2} F_2 \Psi_\lambda (\cdot, q_1) \rangle {\mathrm{d}} q_1. \end{align} $$

According to [16, Lemma 6.8], there is a constant $C(\mu ,V)$ , such that for all $q\in {\mathbb {R}}^2$ and $\psi \in L^2_{\mathrm {s}}({\mathbb {R}}^2)$ with $\lVert \psi \rVert _2=1$

(3.12) $$ \begin{align} \langle \psi, V^{1/2} B_{T}(\cdot, q) V^{1/2} \psi \rangle \leq\langle \psi, O_\mu \psi\rangle \ln \left(\min\left\{\frac{\sqrt{\mu}}{\vert q\vert},\frac{\mu}{T}\right\}\right)\chi_{2<\min\{\mu/T,\sqrt{\mu}/\vert q \vert\}}+ C(\mu,V). \end{align} $$

In combination, we have for $\lambda \to 0$

(3.13) $$ \begin{align} e_\mu \ln \mu/T_c^1(\lambda) \leq \int_{\vert q_1\vert<\sqrt{\mu}/2} \langle F_2 \Psi_\lambda(\cdot , q_1), O_\mu F_2 \Psi_\lambda(\cdot , q_1)\rangle \ln \left(\min\left\{\frac{\sqrt{\mu}}{\sqrt{q_1^2+\eta(\lambda )^2}},\frac{\mu}{T_c^1(\lambda)}\right\}\right){\mathrm{d}} q_1 +O(1). \end{align} $$

We will use this to prove the three parts of the claim.

(1) We want to prove a bound on $\eta (\lambda )$ . Since $e_\mu =\sup \sigma (O_\mu )$ , we can bound

$$\begin{align*}\langle F_2 \Psi_\lambda(\cdot , q_1), O_\mu F_2 \Psi_\lambda(\cdot , q_1)\rangle \leq e_\mu \lVert F_2 \Psi_\lambda(\cdot, q_1)\rVert_2^2. \end{align*}$$

Moreover, clearly $\ln \left (\min \left \{\frac {\sqrt {\mu }}{\sqrt {q_1^2+\eta (\lambda )^2}},\frac {\mu }{T_c^1(\lambda )}\right \}\right ) \leq \ln (\sqrt {\mu }/\eta (\lambda )).$ By equation (3.13) and since $\lVert F_2\Psi _\lambda \rVert _2=1$ , there is a constant c such that $e_\mu \ln (\mu /T_c^1(\lambda ))\leq e_\mu \ln (\sqrt {\mu }/\eta (\lambda )) +c$ for small $\lambda $ . In particular, $\vert \eta (\lambda )\vert \leq \frac {\exp (c/e_\mu )}{\sqrt {\mu }} T_c^1(\lambda )$ , that is, $\eta (\lambda )=O(T_c^1(\lambda ))$ .

(2) We want to bound $\lVert {\mathbb {P}}^\perp F_2 \Psi _\lambda \rVert $ . Denote the ratio of the second highest and the highest eigenvalue of $O_\mu $ by $\alpha $ , where $\alpha <1$ by Assumption 1.2(5). Then

(3.14) $$ \begin{align} \int_{\mathbb{R}} \langle F_2 \Psi_\lambda(\cdot , q_1), O_\mu F_2 \Psi_\lambda(\cdot , q_1)\rangle {\mathrm{d}} q_1 &\leq e_\mu \left( \lVert {\mathbb{P}} F_2 \Psi_\lambda\rVert^2 + \alpha \lVert {\mathbb{P}}^\perp F_2 \Psi_\lambda\rVert^2 \right) \nonumber\\ & =e_\mu \left(\lVert F_2 \Psi_\lambda \rVert^2-(1-\alpha) \lVert {\mathbb{P}}^\perp F_2 \Psi_\lambda \rVert^2 \right) \end{align} $$

Therefore, by equation (3.13)

(3.15) $$ \begin{align} \ln \mu/T_c^1(\lambda)\leq \big(1-(1-\alpha)\lVert {\mathbb{P}}^\perp F_2 \Psi_\lambda\rVert^2 \big)\ln \mu/T_c^1(\lambda) +O(1) \end{align} $$

for $\lambda \to 0$ . This means that $\lVert {\mathbb {P}}^\perp F_2 \Psi _\lambda \rVert ^2 =O(1/\ln \mu /T_c^1(\lambda ))$ . According to Remark 3.1, $\lim _{\lambda \to 0} \lambda \ln \mu /T_c^1(\lambda )=e_\mu ^{-1}$ and thus $\lVert {\mathbb {P}}^\perp F_2 \Psi _\lambda \rVert ^2 =O(\lambda )$ .

(3) In this part, we bound $\lVert {\mathbb {Q}}_\beta ^\perp F_2 \Psi _\lambda \rVert $ . Let

$$\begin{align*}\epsilon(\lambda)=\lVert {\mathbb{Q}}_\beta^\perp F_2 \Psi_\lambda \rVert^2=\int_{{\mathbb{R}}^3} \vert F_2 \Psi_\lambda(r,q_1)\vert^2\chi_{\vert q_1\vert>\sqrt{\mu}\left(\frac{T_c^1(\lambda)}{\mu}\right)^\beta} {\mathrm{d}} r {\mathrm{d}} q_1. \end{align*}$$

By equation (3.13), we have for small $\lambda $

(3.16) $$ \begin{align} e_\mu\ln \mu/T_c^1(\lambda) \leq (1-\epsilon(\lambda ))e_\mu\ln \mu/T_c^1(\lambda)+\epsilon(\lambda) e_\mu \ln \frac{\mu^\beta}{T_c^1(\lambda)^\beta} +C \end{align} $$

for some constant C. Hence,

(3.17) $$ \begin{align} \epsilon(\lambda)\leq \frac{C}{(1-\beta)e_\mu \ln \mu/T_c^1(\lambda) } = O(\lambda), \end{align} $$

where we used $\lim _{\lambda \to 0} \lambda \ln \mu /T_c^1(\lambda )=e_\mu ^{-1}$ (Remark 3.1) in the last step.

3.2 Proof of Lemma 3.4

Proof of Lemma 3.4

The goal is to prove $\lVert \Phi _\lambda \rVert _{L_1^\infty L_{2}^2} <\infty $ , as well as $\lVert \Phi _\lambda ^d \rVert _{L_1^\infty L_{2}^2}=O(1)$ and $\lVert \Phi _{\lambda }^{ex,>}\rVert _{L_1^\infty L_{2}^2}=O(\lambda )$ as $\lambda \to 0$ . If we show $\lVert \Phi _\lambda ^{d} \rVert _{L_1^\infty ({\mathbb {R}}^2) L_{2}^2({\mathbb {R}})} <\infty $ and $\lVert \Phi _\lambda ^{ex} \rVert _{L_1^\infty ({\mathbb {R}}^2) L_{2}^2({\mathbb {R}})} <\infty $ , the Schwarz inequality implies $\lVert \Phi _\lambda \rVert _{L_1^\infty ({\mathbb {R}}^2) L_{2}^2({\mathbb {R}})} <\infty $ .

We shall first prove that $\lVert \Phi _\lambda ^{d} \rVert _{L_1^\infty L_{2}^2} $ is finite and of order $O(1)$ for $\lambda \to 0$ . Using the definition of $\Phi _\lambda ^d$ (3.6), we have

(3.18) $$ \begin{align} & \lVert \Phi_\lambda^d(r,\cdot)\rVert_2^2 \nonumber\\ & =2\lambda^2 \int_{{\mathbb{R}}^5} \overline{\widehat{V^{1/2}\Psi_\lambda}(p',q_1)} B_{T_c^1}(p',(q_1,\eta)) \frac{e^{i (p-p')\cdot r}}{(2\pi)^2} B_{T_c^1}(p,(q_1,\eta))\widehat{V^{1/2}\Psi_\lambda}(p,q_1){\mathrm{d}} p {\mathrm{d}} p' {\mathrm{d}} q_1 \nonumber \\ & \leq 2\lambda^2\sup_{q_1\in {\mathbb{R}}}\sup_{\psi\in L^2({\mathbb{R}}^2),\lVert \psi \rVert_2=1} \int_{{\mathbb{R}}^4} \overline{\widehat{V^{1/2}\psi}(p')} B_{T_c^1}(p',(q_1,\eta)) \frac{e^{i (p-p')\cdot r}}{(2\pi)^2} B_{T_c^1}(p,(q_1,\eta))\widehat{V^{1/2}\psi}(p){\mathrm{d}} p {\mathrm{d}} p' \end{align} $$

For fixed r, the latter integral is the quadratic form corresponding to the projection onto the function $\phi _{q_1}(r')=\frac {1}{2\pi }F_1 B_{T_c^1}(r-r',(q_1,\eta ))V^{1/2}(r')$ . Hence, taking the supremum over $\psi $ , equation (3.18) equals

(3.19) $$ \begin{align} 2\lambda^2\sup_{q_1\in {\mathbb{R}}} \lVert \phi_{q_1}\rVert_2^2=2\lambda^2\sup_{q_1\in {\mathbb{R}}}\int_{{\mathbb{R}}^4} \frac{e^{i (p-p')\cdot r}}{(2\pi)^3} B_{T_c^1}(p,(q_1,\eta))\widehat{V}(p-p')B_{T_c^1}(p',(q_1,\eta)) {\mathrm{d}} p {\mathrm{d}} p'. \end{align} $$

We split the integration into $p^2>2\mu , p^2<2\mu $ and $p^{\prime\, 2}>2\mu , p^{\prime\, 2}<2\mu $ . Using the upper bounds on $B_T$ stated in equation (2.2) leads to the bound

(3.20) $$ \begin{align} \lVert \Phi_\lambda^d(r,\cdot)\rVert_2^2 &\leq \frac{2 \lambda^2}{(2\pi)^3} \Bigg[\lVert \widehat{V}\rVert_\infty \sup_{q_1} \Bigg( \int_{{\mathbb{R}}^2} B_{T_c^1}(p,(q_1,\eta)) \chi_{p^2<2\mu} {\mathrm{d}} p \Bigg)^2 \nonumber\\ &\quad + 2\sup_{q_1} \int_{{\mathbb{R}}^4} B_{T_c^1}(p,(q_1,\eta)) \chi_{p^2<2\mu} |\widehat{V}(p-p')| \frac{C}{1+p^{\prime\, 2}}{\mathrm{d}} p {\mathrm{d}} p' \nonumber\\ &\quad + \int_{{\mathbb{R}}^4}\frac{C}{1+p^2} |\widehat{V}(p-p')| \frac{C}{1+p^{\prime\, 2}}{\mathrm{d}} p {\mathrm{d}} p'\Bigg] \end{align} $$

for a constant C independent of $\lambda $ . We start by considering the first term in the square bracket. Note that $\lVert \widehat {V}\rVert _\infty <\frac {\lVert V\rVert _1}{2\pi }<\infty $ . For fixed $T>0$ , the function $ B_{T}(p,q)$ is bounded, hence the term is finite for fixed $\lambda $ . For $T\to 0$ , we have

(3.21) $$ \begin{align} \sup_{q\in {\mathbb{R}}^2} \int_{{\mathbb{R}}^2} B_{T}(p,q) \chi_{p^2<2\mu} {\mathrm{d}} p =O(\ln \mu/T). \end{align} $$

To see this, we first apply the inequality [12, (6.1)]

(3.22) $$ \begin{align} B_T(p,q)\leq \frac{1}{2}(B_T(p+q,0)+B_T(p-q,0)). \end{align} $$

This gives the upper bound $\sup _{q\in {\mathbb {R}}^2} \int _{{\mathbb {R}}^2} B_{T}(p,0) \chi _{(p-q)^2<2\mu } {\mathrm {d}} p $ . The vector q shifts the disk-shaped domain of integration but does not change its size. In particular, the contribution with $p^2<2\mu $ is bounded above by $ \int _{{\mathbb {R}}^2} B_{T}(p,0) \chi _{p^2<2\mu } {\mathrm {d}} p =O(\ln \mu /T) $ [14, Proposition 3.1] while the contribution with $p^2>2\mu $ is uniformly bounded in T since $B_T(p,0) \chi _{p^2>2\mu }\leq C(\mu )/(1+p^2)$ by equation (2.2). Since for $\lambda \to 0$ , we have $\ln \mu /T_c^1(\lambda )=O(1/\lambda )$ by Remark 3.1, the first term in the square bracket in equation (3.20) is of order $1/\lambda ^2$ as $\lambda \to 0$ . For the second term in the square bracket, we use Hölder’s inequality in $p'$ . By assumption, V is in $L^{t}({\mathbb {R}}^2)$ for some $t>0$ , thus by the Hausdorff–Young inequality we have $\widehat {V}\in L^{t'}$ , where $1=1/t'+1/t$ . Hence, the second term is bounded by

(3.23) $$ \begin{align} 2\sup_{q_1} \int_{{\mathbb{R}}^4} B_{T_c^1}(p,(q_1,\eta)) \chi_{p^2<2\mu}{\mathrm{d}} p \lVert\widehat{V}\rVert_{t'} \left \lVert \frac{C}{1+|\cdot|^2}\right \rVert_{L^{t}({\mathbb{R}}^2)}, \end{align} $$

which is finite for fixed $\lambda $ and of order $O(1/\lambda )$ for $\lambda \to 0$ by equation (3.21). Using Young’s inequality, one sees that the third term in the square bracket is bounded. Taking into account the factor $\lambda ^2$ in front of the square bracket, we conclude that $\lVert \Phi _\lambda ^d(r,\cdot )\rVert _2^2=O(1)$ uniformly in r.

We shall now show that for fixed $\lambda $ , $\lVert \Phi ^{ex}_\lambda \rVert _{L_1^\infty L_{2}^2}<\infty $ and $\lVert \Phi ^{ex,>}_\lambda \rVert _{L_1^\infty L_{2}^2} =O(\lambda )$ as $\lambda \to 0$ . We have

(3.24) $$ \begin{align} \lVert \Phi_\lambda^{ex}(r,\cdot)\rVert_2^2=2\lambda^2 \int_{{\mathbb{R}}^{2d+1}}\overline{ \widehat{V^{1/2}\Psi_\lambda}(( q_1,p_2'), p_1')}B_{T_c^1}& (p',(q_1,\eta)) \frac{e^{i (p-p')\cdot r }}{(2\pi)^{d}} B_{T_c^1}(p,(q_1,\eta)) \nonumber \\ & \quad \times \widehat{V^{1/2}\Psi_\lambda}(( q_1,p_2), p_1) {\mathrm{d}} p {\mathrm{d}} p' {\mathrm{d}} q_1. \end{align} $$

Similarly, we get an expression for $\lVert \Phi ^{ex,>}_\lambda (r,\cdot )\rVert _2^2$ if we multiply the above integrand by the characteristic functions $\chi _{p^2+q_1^2>2\mu } \chi _{p^{\prime\, 2}+q_1^2>2\mu }$ . Using the bounds for $B_T$ in equation (2.2), we bound $\lVert \Phi _\lambda ^{ex}\rVert _{L_1^\infty L_{2}^2}^2$ and $\lVert \Phi ^{ex,>}_\lambda \rVert _{L_1^\infty L_{2}^2}^2$ above by

(3.25) $$ \begin{align} C \lambda^2 \int_{{\mathbb{R}}^{2d+1}}\vert \overline{ \widehat{V^{1/2}\Psi_\lambda}(( q_1,p_2'), p_1')}\vert\frac{1}{1+p^{\prime\, 2}+q_1^2}\frac{1}{1+p^2+q_1^2}\vert \widehat{V^{1/2}\Psi_\lambda}((q_1,p_2),p_1)\vert {\mathrm{d}} p {\mathrm{d}} p' {\mathrm{d}} q_1, \end{align} $$

where the constant C depends on $\mu $ and $\lambda $ for the bound on $\lVert \Phi ^{ex}_\lambda \rVert _{L_1^\infty L_{2}^2}^2$ but is independent of $\lambda $ for the bound on $\lVert \Phi ^{ex,>}_\lambda \rVert _{L_1^\infty L_{2}^2}^2$ . Using the Schwarz inequality in $p_1$ and $p_1'$ and then the bound on the mixed Lebesgue norm in Lemma 3.3, we get the upper bound

(3.26) $$ \begin{align} & C\lambda^2 \lVert \widehat{V^{1/2}\Psi_\lambda} \rVert_{L_1^\infty L_{2}^2}^2 \int_{{\mathbb{R}}^{2d+1}}\left(\int_{\mathbb{R}} \frac{1}{(1+p^{\prime\, 2}+q_1^2)^2}{\mathrm{d}} p^{\prime}_1\right)^{1/2} & \left(\int_{\mathbb{R}} \frac{1}{(1+p^2+q_1^2)^2}{\mathrm{d}} p_1\right)^{1/2} {\mathrm{d}} p_2 {\mathrm{d}} p^{\prime}_2 {\mathrm{d}} q_1 \nonumber \\ &\quad \leq \tilde C \lambda^2 \lVert V\rVert_1 \lVert \Psi_\lambda \rVert_2^2. \end{align} $$

Therefore, $\lVert \Phi ^{ex}_\lambda \rVert _{L_1^\infty L_{2}^2}$ is finite and $\lVert \Phi ^{ex,>}_\lambda \rVert _{L_1^\infty L_{2}^2}=O(\lambda )$ .

3.3 Proof of Lemma 3.5

Proof of Lemma 3.5

The goal is to show that the function $(r,z)\mapsto V^{1/2}(r) \vert \Phi _\lambda (r_1,z_2,z_1)\vert $ is in $L^2({\mathbb {R}}^4)$ and that for $\lambda \to 0$ the $L^2({\mathbb {R}}^4)$ -norms of the functions $V^{1/2}(r) \vert \Phi _\lambda ^{>}(r_1,z_2,z_1)\vert $ , $V^{1/2}(r) \vert \Phi _\lambda ^{d,<}(r_1,z_2,z_1)\vert $ and $V^{1/2}(r) \vert \Phi _\lambda ^{ex,<}(r_1,z_2,z_1)\vert $ are of order $O(\lambda )$ , $O(\lambda ^{-1/2})$ , and $O(\lambda ^{1/2})$ , respectively.

By the Schwarz inequality, it suffices to prove that for $j\in \{d,ex\}$ and $\#\in \{<,>\}$ the integrals $\int _{{\mathbb {R}}^4} V(r) \vert \Phi _\lambda ^{j,\#} (r_1,z_2,z_1)\vert ^2 {\mathrm {d}} r {\mathrm {d}} z$ are finite for all $\lambda _0\geq \lambda>0$ and that as $\lambda \to 0$ , we have $\int _{{\mathbb {R}}^4} V(r) \vert \Phi _\lambda ^{j,>}(r_1,z_2,z_1)\vert ^2 {\mathrm {d}} r {\mathrm {d}} z=O(\lambda ^2)$ for $j\in \{d,ex\}$ , $\int _{{\mathbb {R}}^4} V(r) \vert \Phi _\lambda ^{d,<}(r_1,z_2,z_1)\vert ^2 {\mathrm {d}} r {\mathrm {d}} z=O(\lambda ^{-1})$ and $\int _{{\mathbb {R}}^4} V(r) \vert \Phi _\lambda ^{ex,<}(r_1,z_2,z_1)\vert ^2 {\mathrm {d}} r {\mathrm {d}} z=O(\lambda )$ .

Using the definitions of the different $\Phi _\lambda ^{j,\#}$ (see equations (3.6) and (3.7)), one can rewrite for $\#\in \{<,>\}$

(3.27) $$ \begin{align} & \int_{{\mathbb{R}}^4}V(r)|\Phi_\lambda^{d,\#}(r_1,z_2,z_1) |^2 {\mathrm{d}} r {\mathrm{d}} z= 2\lambda^2 \int_{{\mathbb{R}}^4} \widehat{V}(p_1-p_1',0) B_{T_c^1}((p_1',p_2),(q_1,\eta))\overline{\widehat{ V^{1/2}\Psi_\lambda}( p_1',p_2, q_1) } \nonumber\\ &\qquad\qquad\qquad\quad \times B_{T_c^1}(p,(q_1,\eta))\widehat{ V^{1/2}\Psi_\lambda}(p,q_1) \chi_{p^2+q_1^2\#2\mu}\chi_{p_1^{\prime\, 2}+p_2^2+q_1^2\#2\mu} {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2 {\mathrm{d}} q_1 \end{align} $$

and

(3.28) $$ \begin{align} & \int_{{\mathbb{R}}^4}V(r)|\Phi_\lambda^{ex,\#}(r_1,z_2,z_1) |^2 {\mathrm{d}} r {\mathrm{d}} z =2 \lambda^2 \int_{{\mathbb{R}}^4} \widehat{V}(p_1-p_1',0) B_{T_c^1}((p_1',p_2),(q_1,\eta))\overline{\widehat{ V^{1/2}\Psi_\lambda}(q_1,p_2,p_1')} \nonumber\\ & \qquad\qquad\qquad\qquad\times B_{T_c^1}(p,(q_1,\eta))\widehat{ V^{1/2}\Psi_\lambda}(q_1,p_2, p_1) \chi_{p^2+q_1^2\#2\mu}\chi_{p_1^{\prime\, 2}+p_2^2+q_1^2\#2\mu} {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2 {\mathrm{d}} q_1. \end{align} $$

For $\Phi _\lambda ^{d,>}$ , with the aid of the bound on $B_T$ in equation (2.2) and the estimate for mixed Lebesgue norms in Lemma 3.3 the expression is bounded by

(3.29) $$ \begin{align} C \lambda^2 \lVert V \rVert_1 \int_{{\mathbb{R}}^4} \frac{1}{1+p_1^{\prime\, 2}+p_2^2}\frac{1}{1+p_1^2+p_2^2} \lVert \widehat{V^{1/2}\Psi_\lambda}(\cdot, q_1)\rVert_\infty^2 {\mathrm{d}} q_1 {\mathrm{d}} p_1' & {\mathrm{d}} p_1 {\mathrm{d}} p_2 \leq \tilde C \lambda^2 \lVert V \rVert_1^2 \lVert \Psi_\lambda\rVert_2^2 <\infty, \end{align} $$

where the constants $C,\tilde C$ depend only on $\mu $ . For $\Phi _\lambda ^{ex,>}$ we use the bound on $B_T$ in equation (2.2) and the Schwarz inequality in $p_1$ and $p_1'$ to bound equation (3.28) by

(3.30) $$ \begin{align} C \lambda^2 \lVert V\rVert_1\int_{{\mathbb{R}}^2} \left \lVert \frac{1}{1+|\cdot |^2+p_2^2+q_1^2}\right\rVert_{L^2({\mathbb{R}})}^2 {\mathrm{d}} p_2 {\mathrm{d}} q_1 \lVert \widehat{V^{1/2}\Psi_\lambda}\rVert_{L_p^\infty L_q^2}^2 \leq \tilde C \lambda^2 \lVert V\rVert_1^2\lVert\Psi_\lambda \rVert_2^2, \end{align} $$

where we used the estimate for mixed Lebesgue norms from Lemma 3.3 in the second step. Again, the constants $C,\tilde C$ depend only on $\mu $ .

For $\Phi _\lambda ^{d,<}$ we bound equation (3.27) above by

(3.31) $$ \begin{align} & \frac{\lVert V\rVert_1}{\pi} \lambda^2 \int_{{\mathbb{R}}^4} B_{T_c^1}(p,(q_1,\eta))B_{T_c^1}((p_1',p_2),(q_1,\eta))\lVert \widehat{V^{1/2}\Psi_\lambda} (\cdot,q_1)\rVert_\infty^2 \chi_{p^2+q_1^2<2\mu}\nonumber \\ & \qquad\times\chi_{p_1^{\prime\, 2}+p_2^2+q_1^2<2\mu}{\mathrm{d}} p {\mathrm{d}} p_1' {\mathrm{d}} q_1 \nonumber \\ & \quad\leq \frac{\lVert V\rVert_1^2}{4\pi^3} \lambda^2 \sup_{q_1\in {\mathbb{R}}} \int_{{\mathbb{R}}^3} B_{T_c^1}(p,(q_1,\eta))B_{T_c^1}((p_1',p_2),(q_1,\eta)) \chi_{p^2+q_1^2<2\mu}\chi_{p_1^{\prime\, 2}+p_2^2+q_1^2<2\mu}{\mathrm{d}} p {\mathrm{d}} p_1', \end{align} $$

where we used the bound on mixed Lebesgue norms from Lemma 3.3 and $\lVert \Psi _\lambda \rVert _2=1$ in the second step. For fixed $\lambda $ , this is finite because $B_{T_c^1}$ is a bounded function. For $\lambda \to 0$ , the first part of the following lemma together with the weak coupling asymptotics of $T_c^1$ stated in Remark 3.1 imply that this is of order $O(\lambda ^{-1})$ .

Lemma 3.7. Let $\mu ,C>0$ . For $T\to 0$ , we have

(3.32) $$ \begin{align} \sup_{q,q'\in {\mathbb{R}}^2}\int_{{\mathbb{R}}^3} B_{T}(p,q) B_{T}((p^{\prime}_1,p_2),q'){\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2 =O(\ln \mu/T)^3. \end{align} $$

Furthermore, for every $0<\delta _1<\mu $ there is a $\delta _2>0$ such that for $T\to 0$

(3.33) $$ \begin{align} & \sup_{|q|,|q'|<\delta_2}\int_{{\mathbb{R}}^3}(1-\chi_{\mu-\delta_1<p_2^2<\mu+\delta_1}\chi_{p_1^2<4\delta_1}\chi_{p_1^{\prime\, 2}<4\delta_1}) B_{T}(p,q) B_{T}((p^{\prime}_1,p_2),q') {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2 \nonumber \\ &\quad =O(\ln \mu/T)^{5/2}. \end{align} $$

The second part of this lemma will be used in the proof of Lemma 1.10 to compute the asymptotics of $L_2$ . The proof of Lemma 3.7 can be found in Section 7.2.

For $\Phi _\lambda ^{ex,<}$ we bound equation (3.28) above using the bound on mixed Lebesgue norms in Lemma 3.3 and $\lVert \Psi _\lambda \rVert _2=1$ , which gives

(3.34) $$ \begin{align} \frac{\lambda^2}{2\pi^2} \lVert V\rVert_1^2 \lVert B_{T_c^1}^{{ ex}, 2}(\eta)\rVert, \end{align} $$

where $B_{T}^{{ ex}, 2}(\xi )$ is the operator acting on $L^2(-\sqrt {2\mu },\sqrt {2\mu })$ with integral kernel

(3.35) $$ \begin{align} B_{T}^{{ ex}, 2}(\xi)(p_1',p_1)=\int_{{\mathbb{R}}^2} B_T((p_1',p_2),(q_1,\xi)) B_T(p,(q_1,\xi)) \chi_{q_1^2+p_2^2<2\mu}{\mathrm{d}} q_1 {\mathrm{d}} p_2. \end{align} $$

The superscript 2 indicates that there are two factors of $B_T$ , as opposed to $B_T^{ex}$ which is defined later in equation (5.8). The following lemma together with the asymptotics of $T_c^1(\lambda )$ from Remark 3.1 and the fact that $\eta (\lambda )=O(T_c^1(\lambda ))$ (see Lemma 3.2(1)) implies that equation (3.34) is bounded for fixed $\lambda $ and of order $O(\lambda )$ for $\lambda \to 0$ .

Lemma 3.8. Let $c,\mu>0$ . Then $\sup _{|\xi |<c T}\lVert B_{T}^{{ ex}, 2}(\xi )\rVert $ is finite for all $T>0$ and of order $O(\ln \mu /T)$ as $T\to 0$ .

The proof of Lemma 3.8 is given in Section 7.3.

3.4 Proof of Lemma 3.6

Proof of Lemma 3.6

Recall the functions $g_0$ , $g_+$ and $g_{-}$ on ${\mathbb {R}}^2$ defined as

(3.36)

and

(3.37) $$ \begin{align} g_\pm (p_2,q_2):=\int_{{\mathbb{R}}^2}\overline{\widehat \Phi_\lambda(p,q_1) } \Big[B_{T_c^1}^{-1}(p,q) -B_{T_c^1}^{-1}(p,(q_1,\eta)) \Big] \widehat \Phi_\lambda((p_1,\pm q_2),q_1) {\mathrm{d}} p_1 {\mathrm{d}} q_1. \end{align} $$

We aim to prove that the functions $g_0$ and $g_\pm $ are continuous and bounded and $g_\pm (p_2,\eta )=0$ for all $p_2 \in {\mathbb {R}}$ .

For functions $\psi $ on ${\mathbb {R}}^3$ , let $S\psi (p_1,p_2,q_1)=\psi (p,q_1)+\psi (-p_1,p_2,-q_1)\mp \psi (q_1,p_2,p_1)\mp \psi (-q_1,p_2,-p_1)$ . For $p,q\in {\mathbb {R}}^2$ , let

(3.38) $$ \begin{align} L^0(p,q)&:=\lambda B_{T_c^1}(p,(q_1,\eta)), \end{align} $$

(3.39) $$ \begin{align} L^{\pm}(p,q)&:=\lambda^2 B_{T_c^1}(p,(q_1,\eta))\Big[B_{T_c^1}^{-1}(p,q)-B_{T_c^1}^{-1}(p,(q_1,\eta)) \Big] B_{T_c^1}((p_1,\pm q_2),(q_1,\eta). \end{align} $$

Using the expression for $\widehat {\Phi _\lambda }$ in equation (3.5) obtained from the eigenvalue equation we have

(3.40)

and

(3.41)

Note that $g_\pm (p_2,\eta )=0$ since $L^\pm (p,(q_1,\eta ))=0$ . For measurable functions $\psi _1,\psi _2$ on ${\mathbb {R}}^3$ and $p_2,q_2\in {\mathbb {R}}$ we obtain using the Schwarz inequality in $q_1$

(3.42) $$ \begin{align} & \int_{{\mathbb{R}}^2} |\psi_1(p_1,p_2,q_1)|\frac{1}{1+p_1^2} |\psi_2(p_1,q_2,q_1)| {\mathrm{d}} p_1 {\mathrm{d}} q_1 \nonumber \\ &\quad \leq \int_{{\mathbb{R}}}\frac{1}{1+p_1^2} {\mathrm{d}} p_1 \sup_{p\in {\mathbb{R}}^2}\lVert \psi_1(p,\cdot)\rVert_{ L^2({\mathbb{R}})} \sup_{p\in {\mathbb{R}}^2}\lVert \psi_2(p,\cdot)\rVert_{ L^2({\mathbb{R}})} \end{align} $$

and using the Schwarz inequality in $q_1,p_1$

(3.43) $$ \begin{align} &\int_{{\mathbb{R}}^2} |\psi_1(p_1,p_2,q_1)|\frac{1}{1+p_1^2+q_1^2} | \psi_2(q_1,q_2,p_1)| {\mathrm{d}} p_1 {\mathrm{d}} q_1 \nonumber\\ &\quad \leq \int_{{\mathbb{R}}}\frac{1}{1+p_1^2} {\mathrm{d}} p_1 \sup_{p\in {\mathbb{R}}^2}\lVert \psi_1(p,\cdot)\rVert_{ L^2({\mathbb{R}})} \sup_{p\in {\mathbb{R}}^2}\lVert \psi_2(p,\cdot)\rVert_{ L^2({\mathbb{R}})}. \end{align} $$

There is a constant C independent of $p,q$ (but dependent on $\lambda $ ) such that $L^0(p,q)\leq \frac {C}{1+p_1^2+q_1^2}$ by equation (2.2). Similarly, the bounds on $B_T$ in equation (2.2) and Lemma 2.1 imply that there is a constant C independent of $p,q$ but dependent on $\lambda $ such that

(3.44) $$ \begin{align} L^\pm(p,q)\leq \frac{C(1+p^2+q^2)}{(1+p^2+q_1^2)(1+p_1^2+q^2)}\leq \frac{2C}{1+p_1^2+q_1^2}. \end{align} $$

It follows from equations (3.42) and (3.43) that there is a constant C such that for all measurable functions $\psi _1,\psi _2$ on ${\mathbb {R}}^3$ and $p_2,p_2',q_2,q_2'\in {\mathbb {R}}$

(3.45) $$ \begin{align} & \Big \vert \int_{{\mathbb{R}}^2} \overline{S\psi_1(p,q_1)} L^0(p_1,p_2', q_1, q_2') \psi_2(p_1,q_2,q_1) {\mathrm{d}} p_1 {\mathrm{d}} q_1 \Big \vert \nonumber\\ &\quad \leq C\sup_{p\in {\mathbb{R}}^2}\lVert \psi_1(p,\cdot)\rVert_{ L^2({\mathbb{R}})} \sup_{p\in {\mathbb{R}}^2}\lVert \psi_2(p,\cdot)\rVert_{ L^2({\mathbb{R}})}, \end{align} $$

and similarly

(3.46) $$ \begin{align} &\Big \vert \int_{{\mathbb{R}}^2} \overline{S\psi_1(p,q_1)} L^{\pm}(p_1,p_2', q_1, q_2') S\psi_2(p_1,\pm q_2,q_1) {\mathrm{d}} p_1 {\mathrm{d}} q_1 \Big \vert \nonumber \\ &\quad \leq C\sup_{p\in {\mathbb{R}}^2}\lVert \psi_1(p,\cdot)\rVert_{ L^2({\mathbb{R}})} \sup_{p\in {\mathbb{R}}^2}\lVert \psi_2(p,\cdot)\rVert_{ L^2({\mathbb{R}})}. \end{align} $$

In particular it follows from equations (3.40) and (3.41) with the mixed Lebesgue norm bounds in Lemma 3.3 and the normalization $\lVert V^{1/2}\chi _{\tilde \Omega _1}\Phi _\lambda \rVert _2=1$ that $g_0$ and $g_\pm $ are bounded.

To prove continuity, first note that

(3.47)

where $W_\epsilon (r)=V(r)(e^{-i \epsilon r_2}-1)$ . We only spell out the proof for $g_\pm $ , the argument for $g_0$ is analogous. For all $p_2,q_2\in {\mathbb {R}}$ , we have

(3.48)

Using equation (3.44) it follows by dominated convergence that the last line vanishes as $\epsilon ,\epsilon '\to 0$ . Furthermore, note that by the mixed Lebesgue norm estimates in Lemma 3.3

(3.49)

where $ \lVert \Phi _\lambda \lVert _{L_r^\infty L_{z_1}^2}<\infty $ was shown in Lemma 3.4. Since $\lVert W_\epsilon \Vert _1\leq |\epsilon | \lVert |\cdot |V \rVert _1$ , it follows from equation (3.46) that the first two lines in equation (3.48) vanish as $\epsilon ,\epsilon '\to 0$ . In particular, $g_\pm $ are continuous.

4 Proof of Lemma 1.9

This section contains the proof of Lemma 1.9, where we compute $\lim _{\epsilon \to 0} \langle \psi _\lambda ^\epsilon , UH^{\Omega _2}_{T_c^1(\lambda )}U^\dagger \psi _\lambda ^\epsilon \rangle $ . Recall from (2.6) that

(4.1) $$ \begin{align} t (p_1,q_1,r_1,z_1)=\frac{1}{2}\left(e^{-i(p_1 r_1+q_1 z_1)}+e^{i(p_1 r_1+q_1 z_1)}\mp e^{-i(p_1 z_1+q_1 r_1)} \mp e^{i(p_1 z_1+q_1 r_1)}\right). \end{align} $$

Let $\tilde \Omega _2=\{(r,z)\in {\mathbb {R}}^{2}\times {\mathbb {R}}^{2} \vert \vert r_1\vert < z_1,\vert r_2\vert < z_2\}$ . Analogously to the expression for $UK_T^{\Omega _1}U^\dagger $ in equation (2.7), we have

(4.2) $$ \begin{align} \langle \psi_\lambda^\epsilon, UH^{\Omega_2}_{T}U^\dagger \psi_\lambda^\epsilon \rangle & = \int_{{\mathbb{R}}^{4}}B_{T}(p,q)^{-1} \left|\int_{\tilde\Omega_2}\frac{1}{(2\pi)^2} t (p_1,q_1,r_1,z_1) t (p_2,q_2,r_2,z_2) \psi_\lambda^\epsilon(r,z) {\mathrm{d}} r {\mathrm{d}} z\right|^2{\mathrm{d}} p{\mathrm{d}} q \nonumber\\ &\quad - \lambda \int_{\tilde \Omega_2} V(r)| \psi_\lambda^\epsilon(r,z)|^2 {\mathrm{d}} r {\mathrm{d}} z. \end{align} $$

Since the function $\psi _\lambda ^\epsilon $ defined in equation (1.5) is symmetric under $(r_2,z_2)\to -(r_2,z_2)$ and (anti)symmetric under $(r_2,z_2)\to (z_2,r_2)$ , we have

(4.3) $$ \begin{align} \int_{|r_2|<z_2} t (p_2,q_2,r_2,z_2) \psi_\lambda^\epsilon(r,z) {\mathrm{d}} r_2 {\mathrm{d}} z_2 = \frac{1}{2} \int_{{\mathbb{R}}^2} e^{-i p_2 r_2-i q_2 z_2} \psi_\lambda^\epsilon(r,z) {\mathrm{d}} r_2 {\mathrm{d}} z_2 \end{align} $$

and

(4.4) $$ \begin{align} \int_{|r_2|<z_2} V(r) |\psi_\lambda^\epsilon(r,z)|^2 {\mathrm{d}} r_2 {\mathrm{d}} z_2 = \frac{1}{4} \int_{{\mathbb{R}}^2} (V(r)\chi_{ \vert r_2\vert< \vert z_2\vert }+ V(r_1,z_2)\chi_{\vert z_2\vert < \vert r_2\vert}) |\psi_\lambda^\epsilon(r,z)|^2 {\mathrm{d}} r_2 {\mathrm{d}} z_2. \end{align} $$

Comparing with the expression for $UK_T^{\Omega _1}U^\dagger $ in equation (2.7), we obtain

$$\begin{align*}\langle \psi_\lambda^\epsilon, UH^{\Omega_2}_{T_c^1(\lambda)}U^\dagger \psi_\lambda^\epsilon \rangle=\frac{1}{4} \langle \psi_\lambda^\epsilon, H^{2}_{T_c^1(\lambda)} \psi_\lambda^\epsilon \rangle, \end{align*}$$

where the operator $H_T^2$ is given by

(4.5) $$ \begin{align} H^2_T=UK_T^{\Omega_1}U^\dagger-\lambda V(r)\chi_{ \vert r_2\vert< \vert z_2\vert }-\lambda V(r_1,z_2)\chi_{\vert z_2\vert < \vert r_2\vert} \end{align} $$

acting on $L^2(\tilde \Omega _1\times {\mathbb {R}})$ functions symmetric in r and antisymmetric/symmetric under swapping $r_2\leftrightarrow z_2$ for Dirichlet/Neumann boundary conditions, respectively. Let us define $K_T^2:=UK_T^{\Omega _1}U^\dagger $ .

The trial state $\psi _\lambda ^\epsilon $ has four summands, which we number from one to four in the order they appear in equation (1.5) and refer to as $|j\rangle $ for $j\in \{1,2,3,4\}$ . By symmetry under $(z_2,r_2)\to -(z_2,r_2)$ and $(r_2,z_2)\to (z_2,r_2)$ , we have

(4.6) $$ \begin{align} \langle \psi_\lambda^\epsilon, H^2_{T_c^1} \psi_\lambda^\epsilon \rangle = 4 \sum_{j=1}^4 \langle 1, H^2_{T_c^1} j\rangle. \end{align} $$

For each $j\in \{1,2,3,4\}$ , we write

(4.7) $$ \begin{align} \langle 1, H^2_{T_c^1} j\rangle = \langle 1, (K_{T_c^1}^{2}-\lambda V(r) )j\rangle+\langle 1, ( \lambda V(r) \chi_{|z_2|<|r_2|} +\lambda V(r_1,z_2)\chi_{|r_2|<|z_2|}) j\rangle-\langle 1, \lambda V(r_1,z_2)\ j\rangle. \end{align} $$

We shall prove that

(4.8) $$ \begin{align} \lim_{\epsilon\to 0}\sum_{j=1}^4 \langle 1, (K_{T_c^1}^{2}-\lambda V(r) ) j\rangle=0, \end{align} $$

(4.9) $$ \begin{align} L_1=\lim_{\epsilon\to 0}\sum_{j=1}^4 \langle 1, (V(r) \chi_{|z_2|<|r_2|} + V(r_1,z_2)\chi_{|r_2|<|z_2|} )j\rangle, \end{align} $$

and

(4.10) $$ \begin{align} L_2=-\lim_{\epsilon\to 0}\sum_{j=1}^4 \langle 1, V(r_1,z_2)\ j\rangle, \end{align} $$

where $L_1$ and $L_2$ are the expressions in equations (1.7) and (1.8). In particular, it follows that

$$\begin{align*}\lim_{\epsilon\to 0}\langle \psi_\lambda^\epsilon, U H^{\Omega_2}_{T_c^1} U^\dagger \psi_\lambda^\epsilon \rangle =\lambda(L_1+L_2). \end{align*}$$

4.1 Proof of (4.8):

We argue that all summands vanish as $\epsilon \to 0$ .

j=1: We first show that

(4.11) $$ \begin{align} \langle 1, (K_{T_c^1}^{2}-\lambda V(r) ) 1\rangle = \frac{1}{2\pi}\int_{{\mathbb{R}}^4} \Bigg[ B_{T_c^1}^{-1}(p,(q_1,q_2+\eta)) -B_{T_c^1}^{-1}(p,(q_1,\eta)) \Bigg] \frac{\epsilon^2}{(\epsilon^2+q_2^2)^2}|\widehat{\Phi_\lambda}(p,q_1)|^2{\mathrm{d}} p {\mathrm{d}} q. \end{align} $$

Using eigenvalue equation $K_{T_c^1}^{1}(\eta )\chi _{\tilde \Omega _1}\Phi _\lambda =\lambda V \chi _{\tilde \Omega _1}\Phi _\lambda $ together with the expressions (2.7) and (2.9) for $K_T^{\Omega _1}$ and $K_T^1(q_2)$ , respectively, we observe that

(4.12) $$ \begin{align} & \langle 1, (K_{T_c^1}^{2}-\lambda V(r) ) 1\rangle \nonumber\\ &\quad =\frac{1}{(2\pi)^4}\int_{( \tilde \Omega_1\times {\mathbb{R}})^2\times {\mathbb{R}}^3} \overline{\Phi_\lambda}(r,z_1)\overline{t(p_1,q_1,r_1,z_1)}e^{i p_2 r_2}\Bigg[\int_{\mathbb{R}} B_{T_c^1}^{-1}(p,q) e^{i (\eta-q_2) (z_2'-z_2)-\epsilon (|z_2|+|z_2'|)}{\mathrm{d}} q_2 \nonumber\\ &\qquad -B_{T_c^1}^{-1}(p,(q_1,\eta))e^{-2\epsilon |z_2|} 2\pi \delta(z_2-z_2') \Bigg]t(p_1,q_1,r^{\prime}_1,z_1')e^{-i p_2 r^{\prime}_2}\Phi_\lambda(r',z_1'){\mathrm{d}} r {\mathrm{d}} z {\mathrm{d}} r' {\mathrm{d}} z' {\mathrm{d}} p {\mathrm{d}} q_1 \end{align} $$

We shall carry out the $r,r',z,z'$ integrations. Integration of $\frac {1}{(2\pi )^{3/2}} t\cdot e^{-i p_2 r_2} \Phi _\lambda $ over $r,z_1$ gives $\frac {1}{2} \widehat {\Phi _\lambda }$ (c.f. equation (3.4)), and for the integration over $z_2, z_2'$ , we observe

$$ \begin{align*} \int_{\mathbb{R}} e^{i (\eta-q_2) z_2-\epsilon |z_2|} {\mathrm{d}} z_2&=\frac{2\epsilon}{\epsilon^2+(\eta-q_2)^2}, \\ 2\pi \int_{\mathbb{R}} e^{-2\epsilon |z_2|}=2\pi \epsilon^{-1}&= \int_{\mathbb{R}} \frac{4\epsilon^2}{(\epsilon^2+(\eta-q_2)^2)^2} {\mathrm{d}} q_2. \end{align*} $$

In total, we obtain

(4.13) $$ \begin{align} \langle 1,( K_{T_c^1}^{2}-\lambda V(r) ) 1\rangle = \frac{1}{2\pi}\int_{{\mathbb{R}}^4}\Bigg[ B_{T_c^1}^{-1}(p,q) -B_{T_c^1}^{-1}(p,(q_1,\eta)) \Bigg] \frac{\epsilon^2}{(\epsilon^2+(\eta-q_2)^2)^2} |\widehat{\Phi_\lambda}(p,q_1)|^2 {\mathrm{d}} p {\mathrm{d}} q \end{align} $$

and substituting $q_2\to q_2+\eta $ we arrive at equation (4.11).

For $|q_2|>1$ , using $B_T^{-1}(p,q)\leq \tilde C (1+p^2+q^2)$ (see Lemma 2.1), we bound the integrand in equation (4.11) above by $\frac {C \epsilon ^2 (1+p^2+q_1^2)}{q_2^2}|\widehat {\Phi _\lambda }(p,q_1)|^2$ . Since $\Phi _\lambda \in H^1({\mathbb {R}}^3)$ , the integral vanishes as $\epsilon \to 0$ . For $|q_2|<1$ , substitute $q_2\to \epsilon q_2$ and use that

$$\begin{align*}q_2^{-1}( B_{T_c^1}^{-1}(p,(q_1,q_2+\eta) -B_{T_c^1}^{-1}(p,(q_1,\eta))) =-f(p,(q_1,\eta),q_2) B_{T_c^1}^{-1}(p,(q_1,q_2+\eta) B_{T_c^1}^{-1}(p,(q_1,\eta)), \end{align*}$$

where f is defined as in Lemma 2.2. The integral then equals

(4.14) $$ \begin{align} -\frac{1}{2\pi}\int_{{\mathbb{R}}^4}\chi_{|q_2|<\epsilon^{-1}} f(p,(q_1,\eta),\epsilon q_2) B_{T_c^1}^{-1}(p,(q_1,\epsilon q_2+\eta) B_{T_c^1}^{-1}(p,(q_1,\eta)) \frac{q_2}{(1+q_2^2)^2}|\widehat{\Phi_\lambda}(p,q_1)|^2{\mathrm{d}} p {\mathrm{d}} q. \end{align} $$

By Lemma 2.2 and Lemma 2.1, the integrand is bounded above by the integrable function

(4.15) $$ \begin{align} C (1+p^2+q_1^2) \frac{|q_2|}{(1+q_2^2)^2}|\widehat{\Phi_\lambda}(p,q_1)|^2. \end{align} $$

Thus, by dominated convergence, continuity of f and $B_T$ and since $\int _{\mathbb {R}} \frac {q_2}{(1+q_2^2)^2} {\mathrm {d}} q_2=0$ , we have $\lim _{\epsilon \to 0} \langle 1, K_{T_c^1}^{2}-\lambda V(r) 1\rangle =0$ .

j=2: We distinguish the cases $\eta (\lambda )=0$ and $\eta (\lambda )\neq 0$ . If $\eta (\lambda )=0$ , $\Phi _\lambda (r,z_1)$ is either even or odd in $r_2$ . The term for $j=2$ hence agrees with the term for $j=1$ or its negative and hence vanishes in the limit. For $\eta (\lambda )\neq 0$ , the intuition is that integration over $z_2,z_2'$ approximately gives a product of delta functions $\delta (q_2-\eta )\delta (q_2+\eta )=0$ . Using that the integral of $\frac {1}{(2\pi )^{3/2}} t \cdot e^{-i p_2 r_2} \Phi _\lambda $ over $r,z_1$ gives $\frac {1}{2} \widehat {\Phi _\lambda }$ (see (3.4)) and $e^{-i p_2 r_2}=e^{-i (-p_2)(-r_2)}$ we have

(4.16) $$ \begin{align} & \langle 1, ( K_{T_c^1}^{2}-\lambda V(r) )2\rangle \nonumber\\ &\quad =\frac{1}{8\pi}\int_{{\mathbb{R}}^6}\overline{\widehat \Phi_\lambda(p,q_1) } B_{T_c^1}^{-1}(p,q) e^{-i (\eta-q_2) z_2-i (\eta+q_2) z_2'-\epsilon (|z_2|+|z_2'|)}\widehat \Phi_\lambda((p_1,-p_2),q_1){\mathrm{d}} z_2 {\mathrm{d}} z_2' {\mathrm{d}} p {\mathrm{d}} q \nonumber\\ &\qquad -\int_{\tilde \Omega_1\times {\mathbb{R}}} \overline{\Phi_\lambda(r,z_1)} \lambda V(r) \Phi_\lambda(r_1,-r_2,z_1) e^{-2i \eta z_2-2\epsilon |z_2|} {\mathrm{d}} r {\mathrm{d}} z. \end{align} $$

Carrying out the $z_2$ and $z_2'$ integrations gives

(4.17) $$ \begin{align} & \langle 1, (K_{T_c^1}^{2}-\lambda V(r) ) 2\rangle \nonumber\\ &\quad =\frac{1}{2\pi}\int_{{\mathbb{R}}^4}\overline{\widehat \Phi_\lambda(p,q_1) } B_{T_c^1}^{-1}(p,q) \frac{\epsilon^2}{(\epsilon^2+(\eta-q_2)^2)(\epsilon^2+(\eta+q_2)^2)}\widehat \Phi_\lambda((p_1,-p_2),q_1){\mathrm{d}} p {\mathrm{d}} q \nonumber\\ & \qquad -\int_{\tilde \Omega_1} \overline{\Phi_\lambda(r,z_1)} \lambda V(r) \Phi_\lambda(r_1,-r_2,z_1) \frac{\epsilon}{\epsilon^2+\eta^2} {\mathrm{d}} r {\mathrm{d}} z_1. \end{align} $$

Using the Schwarz inequality in the $r_2$ variable, we bound the absolute value of the second term by $\frac { \epsilon \lambda }{\eta ^2}\int _{\tilde \Omega _1}V(r)\vert \Phi _\lambda (r,z_1)|^2 {\mathrm {d}} r {\mathrm {d}} z_1 \leq \frac { \epsilon \lambda }{\eta ^2}\lVert V\rVert _1 \lVert \Phi _\lambda \rVert _{L_1^\infty L_{2}^2}^2$ . It was shown in Lemma 3.4 that $ \lVert \Phi _\lambda \rVert _{L_1^\infty L_{2}^2}<\infty $ and hence the term vanishes for $\epsilon \to 0$ . To bound the absolute value of the first term in equation (4.17), we first use that $B_T^{-1}(p,q)\leq C(1+p^2+q^2)$ by Lemma 2.1 and the Schwarz inequality in the $p_2$ variable and then use symmetry to restrict to $q_2>0$ and distinguish the cases $|q_2-\eta |\lessgtr \epsilon $ :

(4.18) $$ \begin{align} & C \int_{{\mathbb{R}}^4} \frac{\epsilon^2(1+p^2+q^2)}{(\epsilon^2+(\eta-q_2)^2)(\epsilon^2+(\eta+q_2)^2)}|\widehat \Phi_\lambda(p,q_1)|^2{\mathrm{d}} p {\mathrm{d}} q \nonumber\\ &\quad \leq 2C \int_{{\mathbb{R}}^3} \Bigg(\int_0^\infty \Bigg[\frac{\chi_{|q_2-\eta|<\epsilon}(1+p^2+q^2)}{(\eta-q_2)^2+(\eta+q_2)^2}+ \frac{\chi_{|q_2-\eta|>\epsilon}\epsilon^2(1+p^2+q^2)}{(\eta-q_2)^2(\eta+q_2)^2}\Bigg] {\mathrm{d}} q_2 \Bigg)|\widehat \Phi_\lambda(p,q_1)|^2{\mathrm{d}} p {\mathrm{d}} q_1. \end{align} $$

There is a constant $C(\eta )$ such that the first term in the square brackets is bounded above by $C(\eta )\chi _{|q_2-\eta |<\epsilon }(1+p^2+q_1^2)$ , and the second term is bounded by $C(\eta )\frac {\chi _{|q_2-\eta |>\epsilon }\epsilon ^2(1+p^2+q_1^2)}{(\eta -q_2)^2}$ . This gives the upper bound

(4.19) $$ \begin{align} \tilde C \Bigg(\int_0^\infty \Bigg[\chi_{|q_2-\eta|<\epsilon}+ \frac{\chi_{|q_2-\eta|>\epsilon}\epsilon^2}{(\eta-q_2)^2}\Bigg] {\mathrm{d}} q_2 \Bigg) \lVert \Phi_\lambda\rVert_{H^1({\mathbb{R}}^3)}^2. \end{align} $$

The remaining integral is of order $O(\epsilon )$ as $\epsilon \to 0$ , and thus the term vanishes in the limit $\epsilon \to 0$ .

j=3,4: Using the eigenvalue equation $K_{T_c^1(\lambda )}^{1}(\eta )\chi _{\tilde \Omega _1} \Phi _\lambda =\lambda V\chi _{\tilde \Omega _1} \Phi _\lambda $ and that the integral of $\frac {1}{(2\pi )^{3/2}}t\cdot \Phi _\lambda $ over the spatial variables gives $\frac {1}{2}\widehat {\Phi _\lambda }$ (see equation (3.4)), we have

(4.20) $$ \begin{align} & | \langle 1, (K_{T_c^1}^{2}-\lambda V(r)) j\rangle| \nonumber\\ &\quad =\Big \vert \frac{1}{8\pi}\int_{{\mathbb{R}}^6}\overline{\widehat \Phi_\lambda(p,q_1) } \left(B_{T_c^1}^{-1}(p,q)-B_{T_c^1}^{-1}(p,(q_1,\eta))\right) e^{-i (\eta-q_2) z_2-i (\mp \eta+p_2) r_2'-\epsilon (|z_2|+|r_2'|)} \nonumber\\ &\qquad \times \widehat \Phi_\lambda((p_1,\pm q_2),q_1){\mathrm{d}} z_2 {\mathrm{d}} r_2' {\mathrm{d}} p {\mathrm{d}} q\Big \vert, \end{align} $$

where the upper signs correspond to $j=3$ and the lower ones to $j=4$ , respectively. Carrying out the integration over $r_2'$ and $z_2$ and substituting $q_2\to \epsilon q_2+\eta , p_2\to \epsilon p_2\pm \eta $ we obtain

(4.21) $$ \begin{align} & | \langle 1, (K_{T_c^1}^{2}-\lambda V(r)) j\rangle| \nonumber\\ &\qquad =\Big \vert\frac{1}{2\pi}\int_{{\mathbb{R}}^4}\overline{\widehat \Phi_\lambda((p_1,\epsilon p_2\pm \eta),q_1) } \frac{1}{1+ p_2^2}\frac{1}{1+q_2^2}\Big[B_{T_c^1}^{-1}((p_1,\epsilon p_2\pm \eta),(q_1,\epsilon q_2+\eta)) \nonumber\\ &\qquad\qquad\qquad\qquad\qquad\quad -B_{T_c^1}^{-1}((p_1,\epsilon p_2\pm \eta),(q_1,\eta)) \Big] \widehat \Phi_\lambda((p_1,\pm(\epsilon q_2+ \eta)),q_1) {\mathrm{d}} p {\mathrm{d}} q\Big \vert. \end{align} $$

With the definition of $g_\pm $ as in Lemma 3.6, the latter equals

(4.22) $$ \begin{align} \Big \vert\frac{1}{2\pi}\int_{{\mathbb{R}}^2} \frac{g_{\pm}(\epsilon p_2\pm \eta ,\epsilon q_2+\eta)}{(1+ p_2^2)(1+q_2^2)}{\mathrm{d}} p_2 {\mathrm{d}} q_2\Big \vert. \end{align} $$

With Lemma 3.6, it follows by dominated convergence that $\lim _{\epsilon \to 0} \langle 1, ( K_{T_c^1}^{2}-\lambda V(r) )j\rangle =0$ .

4.2 Proof of equation (5.9):

We have

(4.23) $$ \begin{align} & \sum_{j=1}^4 \langle 1, (V(r) \chi_{|z_2|<|r_2|} + V(r_1,z_2)\chi_{|r_2|<|z_2|} )j\rangle =\int_{\tilde \Omega_1\times {\mathbb{R}}}(V(r)\chi_{|z_2|<|r_2|}+V(r_1,z_2)\chi_{|r_2|<|z_2|} ) \overline{\Phi_\lambda(r,z_1)} \nonumber\\ &\qquad \times \Big(\Phi_\lambda(r,z_1)e^{-2\epsilon|z_2|}+ \Phi_\lambda(r_1,-r_2,z_1)e^{-2\epsilon|z_2|-2i\eta z_2} \mp \Phi_\lambda(r_1,z_2,z_1)e^{-\epsilon(|r_2|+|z_2|)-i\eta(z_2- r_2)} \nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad \mp \Phi_\lambda(r_1,- z_2,z_1)e^{-\epsilon(|r_2|+|z_2|)-i\eta(z_2+ r_2)}\Big){\mathrm{d}} r {\mathrm{d}} z. \end{align} $$

The claim follows from dominated convergence provided that

(4.24) $$ \begin{align} \int_{{\mathbb{R}}^4}(V(r)\chi_{|z_2|<|r_2|}+V(r_1,z_2)\chi_{|r_2|<|z_2|} )|\Phi_\lambda(r,z_1)|&\Big(|\Phi_\lambda(r,z_1)|+ |\Phi_\lambda(r_1,-r_2,z_1)| \nonumber\\ & +| \Phi_\lambda(r_1,z_2,z_1)|+| \Phi_\lambda(r_1,- z_2,z_1)|\Big){\mathrm{d}} r {\mathrm{d}} z \end{align} $$

is finite. Using the Schwarz inequality in $z_1$ and carrying out the integration over $z_2$ , this is bounded above by

(4.25) $$ \begin{align} 4 \int_{{\mathbb{R}}^3}(V(r)\chi_{|z_2|<|r_2|}+V(r_1,z_2)\chi_{|r_2|<|z_2|} ) \lVert \Phi_\lambda \rVert_{L_1^\infty L_{2}^2}{\mathrm{d}} r {\mathrm{d}} z_2 \leq 16 \int_{{\mathbb{R}}^2} V(r)|r_2|{\mathrm{d}} r \lVert \Phi_\lambda \rVert_{L_1^\infty L_{2}^2}. \end{align} $$

This is finite since $\lVert \Phi _\lambda \rVert _{L_1^\infty L_{2}^2}<\infty $ was shown in Lemma 3.4 and $|\cdot |V \in L^1$ by assumption.

4.3 Proof of equation (4.10):

j=1,2: We have

(4.26) $$ \begin{align} \langle 1, V(r_1,z_2) 1\rangle=\int_{\tilde \Omega_1\times {\mathbb{R}}} V(r_1,z_2)|\Phi_\lambda(r,z_1)|^2e^{-2\epsilon|z_2|}{\mathrm{d}} r {\mathrm{d}} z \end{align} $$

and

(4.27) $$ \begin{align} \langle 1, V(r_1,z_2) 2\rangle=\int_{\tilde \Omega_1\times {\mathbb{R}}} V(r_1,z_2) \overline{\Phi_\lambda(r,z_1)}\Phi_\lambda(r_1,-r_2,z_1)e^{-2\epsilon|z_2|-2i\eta z_2}{\mathrm{d}} r {\mathrm{d}} z. \end{align} $$

In both cases, we can apply dominated convergence since $V(r_1,z_2)|\Phi _\lambda (r,z_1)|^2\in L^1({\mathbb {R}}^4)$ by Lemma 3.5 (and using additionally the Schwarz inequality in the second case) and obtain the first two terms in $L_2$ .

j=3,4: We start with the case of Neumann boundary conditions. Rewriting the expression in momentum space, we have

(4.28)

where the upper/lower signs correspond to $j=3$ and $j=4$ , respectively, and $g_0$ is defined as in Lemma 3.6. It follows from Lemma 3.6, dominated convergence and $\int _{\mathbb {R}} \frac {1}{1+x^2} {\mathrm {d}} x = \pi $ that

(4.29) $$ \begin{align} \lim_{\epsilon\to0} \langle 1, V(r_1,z_2) j\rangle=2\pi g_0(\pm \eta,\pm \eta ). \end{align} $$

For Dirichlet boundary conditions, this comes with a minus sign.

5 Weak coupling asymptotics

In this section, we shall prove Lemma 1.10. We prove the desired asymptotic bounds $L_1=O(1)$ and $L_2\leq -C/\lambda $ as $\lambda \to 0$ in Sections 5.1 and 5.2, respectively.

5.1 Asymptotics of $L_1$

We recall the definition of $L_1$

(5.1) $$ \begin{align} L_1 & = \int_{\tilde \Omega_1\times {\mathbb{R}}} \chi_{\vert z_2\vert <\vert r_2\vert}V(r)\Bigg(\vert \Phi_\lambda(r_1,r_2,z_1)\vert^2+\vert \Phi_\lambda(r_1,z_2,z_1)\vert^2 \nonumber\\ &\qquad +\overline{\Phi_\lambda(r_1,r_2,z_1)}\Phi_\lambda(r_1,-r_2,z_1)e^{-2i\eta(\lambda) z_2} +\overline{\Phi_\lambda(r_1,z_2,z_1)}\Phi_\lambda(r_1,-z_2,z_1)e^{-2i\eta(\lambda) r_2} \nonumber\\ &\quad \mp \overline{\Phi_\lambda(r_1,r_2,z_1)}\Phi_\lambda(r_1,z_2,z_1)e^{i\eta(\lambda)(r_2- z_2)} \mp \overline{\Phi_\lambda(r_1,z_2,z_1)}\Phi_\lambda(r_1,r_2,z_1)e^{-i\eta(\lambda) (r_2-z_2)} \nonumber\\ & \mp \overline{\Phi_\lambda(r_1,r_2,z_1)}\Phi_\lambda(r_1,-z_2,z_1)e^{-i\eta(\lambda)(r_2+ z_2)} \mp \overline{\Phi_\lambda(r_1,z_2,z_1)}\Phi_\lambda(r_1,-r_2,z_1)e^{i\eta(\lambda) (-r_2+z_2)} \Bigg){\mathrm{d}} r {\mathrm{d}} z. \end{align} $$

The goal is to show that $ L_1$ is of order $O(1)$ as $\lambda \to 0$ . By the Schwarz inequality, it suffices to prove that $ \int _{\tilde \Omega _1\times {\mathbb {R}}} \chi _{|z_2|<|r_2|} V(r) (|\Phi _\lambda (r_1,r_2,z_1)|^2 +|\Phi _\lambda (r_1,z_2,z_1)|^2){\mathrm {d}} r {\mathrm {d}} z=O(1)$ . Furthermore, since $\Phi _\lambda =\Phi _\lambda ^d\mp \Phi _\lambda ^{ex,<}\mp \Phi _\lambda ^{ex,>}$ (see equations (3.6) and (3.7) for the definitions), again by the Schwarz inequality it suffices to prove

(5.2) $$ \begin{align} \int_{ \tilde \Omega_1\times {\mathbb{R}}} \chi_{|z_2|<|r_2|} V(r) |\Phi^j_\lambda(r_1,r_2,z_1)|^2 {\mathrm{d}} r {\mathrm{d}} z =O(1) \end{align} $$

and

(5.3) $$ \begin{align} \int_{ \tilde \Omega_1\times {\mathbb{R}}} \chi_{|z_2|<|r_2|} V(r) |\Phi^j_\lambda(r_1,z_2,z_1)|^2 {\mathrm{d}} r {\mathrm{d}} z =O(1) \end{align} $$

for $j\in \{d,(ex,<),(ex,>)\}$ .

Case $j\in \{d,(ex,>)\}$ : In Lemma 3.4, we show that $\sup _{r\in {\mathbb {R}}^2}\int _{\mathbb {R}} |\Phi ^j_\lambda (r,z_1)|^2{\mathrm {d}} z_1 = O(1)$ . Both equations (5.2) and (5.3) follow since $|\cdot | V \in L^1$ .

Case $j=(ex,<)$ : Let $W_1(r):=2|r_2| V(r)$ and $W_2(r):=\int _{{\mathbb {R}}} V(r_1,z_2)\chi _{|r_2|<|z_2|} {\mathrm {d}} z_2$ . We have $W_1,W_2\in L^1({\mathbb {R}}^2)$ . Note that

(5.4) $$ \begin{align} \int_{ \tilde \Omega_1\times {\mathbb{R}}} \chi_{|z_2|<|r_2|} V(r) |\Phi^{ex,<}_\lambda(r_1,r_2,z_1)|^2 {\mathrm{d}} r {\mathrm{d}} z = \int_{\tilde \Omega_1} W_1(r) |\Phi^{ex,<}_\lambda(r_1,r_2,z_1)|^2 {\mathrm{d}} r {\mathrm{d}} z_1 \end{align} $$

and

(5.5) $$ \begin{align} \int_{\tilde \Omega_1\times {\mathbb{R}}} \chi_{|z_2|<|r_2|} V(r) |\Phi^{ex,<}_\lambda(r_1,z_2,z_1)|^2 {\mathrm{d}} r {\mathrm{d}} z =\int_{\tilde \Omega_1} W_2(r) |\Phi^{ex,<}_\lambda(r_1,r_2,z_1)|^2 {\mathrm{d}} r {\mathrm{d}} z_1, \end{align} $$

where we renamed $z_2\leftrightarrow r_2$ . For any $L^1$ -function $W\geq 0$ , we have

(5.6) $$ \begin{align} & \left(\int_{\tilde \Omega_1} W(r) |\Phi^{ex,<}_\lambda(r_1,r_2,z_1)|^2 {\mathrm{d}} r {\mathrm{d}} z_1\right)^{1/2}\nonumber\\ &\quad =\lVert W^{1/2} \Phi^{ex,<}_\lambda \rVert_2=\sup_{\psi\in L^2(\tilde \Omega_1),\lVert \psi\rVert_2=1}| \langle \psi, W^{1/2} \Phi^{ex,<}_\lambda\rangle| \nonumber\\ &\quad \leq \sqrt{2}\lambda \sup_{\psi_1,\psi_2\in L^2({\mathbb{R}}^3),\lVert \psi_1\rVert=\lVert \psi_2\rVert=1}\int_{{\mathbb{R}}^3}\big| \widehat{W^{1/2} \psi_1}(p,q_1) B_{T_c^1}(p,(q_1,\eta)) \chi_{p_2^2<2\mu} \nonumber\\ &\qquad\times\widehat{V^{1/2} \psi_2}(( q_1,p_2), p_1)\big| {\mathrm{d}} p {\mathrm{d}} q_1, \end{align} $$

where we used the definition of $\Phi ^{ex,<}_\lambda $ (see equation (3.7)) and the normalization $\lVert \Psi _\lambda \rVert =1$ in the last step. We bound $|\widehat {W^{1/2} \psi _1}(p,q_1)|\leq \lVert W \rVert _1^{1/2} \lVert F_2\psi _1(\cdot ,q_1)\rVert _2$ , and similarly for $|\widehat {V^{1/2} \psi _2}(p,q_1)|$ . Thus, equation (5.6) is bounded above by

(5.7) $$ \begin{align} \sqrt{2}\lambda \lVert W \rVert_1^{1/2}\lVert V \rVert_1^{1/2}\lVert B_T^{ex}(\eta) \rVert, \end{align} $$

where $B_T^{ ex}(q_2)$ is the operator on $L^2({\mathbb {R}})$ with integral kernel

(5.8) $$ \begin{align} B_T^{ ex}(q_2)(p_1,q_1)=\int_{\mathbb{R}} B_{T}(p,q)\chi_{p_2^2<2\mu} {\mathrm{d}} p_2. \end{align} $$

It was shown in [16, Proof of Lemma 6.1] (see equation (5.16) and rest of argument), that

(5.9) $$ \begin{align} \sup_T \sup_{q_2} \lVert B_T^{ ex}(q_2)\rVert<\infty. \end{align} $$

In particular, we conclude that $\int _{\tilde \Omega _1} W_k(r) |\Phi ^{ex,<}_\lambda (r_1,r_2,z_1)|^2 {\mathrm {d}} r {\mathrm {d}} z_1 =O(\lambda ^2)$ for $k\in \{1,2\}$ .

5.2 Asymptotics of $L_2$

Recall that

(5.10)

The goal is to prove that $L_2$ diverges like $-\lambda ^{-1}$ to negative infinity as $\lambda \to 0$ . We shall prove that the second line in equation (5.10) is of order $O(1)$ as $\lambda \to 0$ . For the first line in equation (5.10), we shall prove that it is bounded above by $-c\lambda ^{-1}$ for some $c>0$ as $\lambda \to 0$ .

Second line of equation (5.10): Let $\xi \in \{\eta ,-\eta \}$ . Consider the expression

which agrees with $|g_0(\xi , \xi )|$ in equation (3.8). Recalling the expression for $g_0$ in equation (3.40) involving $L^0$ and S defined at the beginning of Section 3.4, we have

(5.11)

Using the Schwarz inequality and this is bounded above by

(5.12)

where in the second step we used that $\int _{\mathbb {R}} B_{T_c^1}((p_1,\xi ),(q_1,\eta )) {\mathrm {d}} p_1$ acts as multiplication operator on . Using the bound on the mixed Lebesgue norm in Lemma 3.3 and since $\lVert V^{1/2} \chi _{\tilde \Omega _1} \Phi _\lambda \rVert _2=1$ , we have . The following lemma together with the weak coupling asymptotics of $T_c^1(\lambda )$ and $\eta (T)$ in Remark 3.1 and Lemma 3.2(1) imply that equation (5.12) is of order $O(1)$ .

Lemma 5.1. Let $\xi (T),\xi '(T)$ be functions of T with $\lim _{T\to 0} \xi (T)=\lim _{T\to 0} \xi '(T)=0$ . Then as $T\to 0$ ,

(5.13) $$ \begin{align} \sup_{q_1}\int_{{\mathbb{R}}} B_{T}((p_1,\xi(T)),(q_1,\xi'(T))){\mathrm{d}} p_1 =O(\ln \mu/T). \end{align} $$

The proof can be found in Section 7.4.

First line of equation (5.10): Recall from Section 4 that $\Phi _\lambda =\Phi _\lambda ^{>}+\Phi _\lambda ^{d,<}\mp \Phi _\lambda ^{ex,<}$ . We show in Lemma 3.5 that the $L^2$ -norms of $V^{1/2}(r)\Phi _\lambda ^{>}(r_1,z_2,z_1)$ , $V^{1/2}(r)\Phi _\lambda ^{d,<}(r_1,z_2,z_1)$ , and $V^{1/2}(r)\Phi _\lambda ^{ex,<}(r_1,z_2,z_1)$ are of order $O(\lambda )$ , $O(\lambda ^{-1/2})$ , and $O(\lambda ^{1/2})$ , respectively. It follows with the Schwarz inequality that the first line of $L_2$ in equation (5.10) equals

(5.14) $$ \begin{align} - \int_{\tilde \Omega_1\times {\mathbb{R}}} V(r)\Bigg(\vert \Phi_\lambda^{d,<}(r_1,z_2,z_1)\vert^2 +\overline{\Phi_\lambda^{d,<}(r_1,z_2,z_1)}\Phi_\lambda^{d,<}(r_1,-z_2,z_1)e^{-2i\eta(\lambda) r_2}\Bigg) {\mathrm{d}} r {\mathrm{d}} z +O(1) \end{align} $$

Note that $\Phi _\lambda ^{d,<}(r_1,z_2,z_1)=\Phi _\lambda ^{d,<}(-r_1,z_2,-z_1)$ . We rewrite the expression in equation (5.14) as

(5.15) $$ \begin{align} & -\frac{1}{2}\int_{{\mathbb{R}}^4} V(r)\overline{\Phi_\lambda^{d,<}(r_1,z_2,z_1)}\Bigg( \Phi_\lambda^{{d,<}}(r_1,z_2,z_1)+\Phi_\lambda^{{d,<}}(r_1,-z_2,z_1)e^{-2i\eta(\lambda) r_2}\Bigg) \chi_{|r_1|<|z_1|} {\mathrm{d}} r {\mathrm{d}} z \nonumber\\ &\qquad =-\frac{1}{2}\int_{{\mathbb{R}}^4}V(r)\overline{\Phi_\lambda^{d,<}(r_1,z_2,z_1)}\Bigg( \Phi_\lambda^{{d,<}}(r_1,z_2,z_1)+\Phi_\lambda^{{d,<}}(r_1,-z_2,z_1)e^{-2i\eta(\lambda) r_2}\Bigg) {\mathrm{d}} r {\mathrm{d}} z \nonumber\\ & +\frac{1}{2}\int_{{\mathbb{R}}^4} V(r)\overline{\Phi_\lambda^{d,<}(r_1,z_2,z_1)}\Bigg( \Phi_\lambda^{{d,<}}(r_1,z_2,z_1)+\Phi_\lambda^{{d,<}}(r_1,-z_2,z_1)e^{-2i\eta(\lambda) r_2}\Bigg) \chi_{|z_1|<|r_1|} {\mathrm{d}} r {\mathrm{d}} z. \end{align} $$

We first consider the last line in equation (5.15) with the restriction to $|z_1|<|r_1|$ . We prove that this term is of order $O(1)$ as $\lambda \to 0$ . Second, we will prove that the expression on the second line in equation (5.15) is bounded above by $-c \lambda ^{-1}$ for some constant $c>0$ as $\lambda \to 0$ .

Asymptotics of third line in equation (5.15): Define $W\in L^1({\mathbb {R}}^3)$ by $W(r,z_1):= V(r) \chi _{|z_1|<|r_1|}$ . By the Schwarz inequality, it suffices to prove that $\int _{{\mathbb {R}}^4}W(r,z_1)|\Phi _\lambda ^{d,<}(r_1,z_2,z_1)|^2 {\mathrm {d}} r {\mathrm {d}} z=O(1)$ for $\lambda \to 0$ . Using the definition of $\Phi _\lambda ^{d,<}$ , we have

(5.16) $$ \begin{align} & \int_{{\mathbb{R}}^4}W(r,z_1)|\Phi_\lambda^{d,<}(r_1,z_2,z_1)|^2 {\mathrm{d}} r {\mathrm{d}} z \nonumber\\ &\quad =\frac{2\lambda^2}{(2\pi)^{1/2}} \int_{{\mathbb{R}}^5} \widehat{W}((p_1-p_1',0),q_1-q_1')B_{T_c^1}(p,(q_1,\eta)) \nonumber\\ &\qquad \times \overline{\widehat{V^{1/2}\Psi_\lambda}(p,q_1)}B_{T_c^1}((p^{\prime}_1,p_2),(q^{\prime}_1,\eta)) \widehat{V^{1/2}\Psi_\lambda}(p^{\prime}_1,p_2,q^{\prime}_1)\chi_{p^2+q_1^2< 2\mu}\chi_{p_1^{\prime\, 2}+p_2^2+q_1^{\prime\, 2}< 2\mu}{\mathrm{d}} p {\mathrm{d}} p_1' {\mathrm{d}} q_1 {\mathrm{d}} q_1'. \end{align} $$

Using $|\widehat {W}(p,q_1)|\leq \frac {\lVert W \rVert _1}{(2\pi )^{3/2}}$ and $\lVert \widehat {V^{1/2}\Psi _\lambda }(\cdot ,q_1)\rVert _\infty \leq \lVert V\rVert _1^{1/2} \lVert F_2 \Psi _\lambda (\cdot ,q_1)\rVert _2$ , we bound this from above by

(5.17) $$ \begin{align} & \frac{\lambda^2}{2\pi^2}\lVert W \rVert_1 \lVert V\rVert_1\int_{{\mathbb{R}}^5} B_{T_c^1}(p,(q_1,\eta)) B_{T_c^1}((p^{\prime}_1,p_2),(q^{\prime}_1,\eta))\chi_{p^2+q_1^2< 2\mu}\chi_{p_1^{\prime\, 2}+p_2^2+q_1^{\prime\, 2}< 2\mu} \nonumber\\ &\qquad \times \lVert F_2\Psi_\lambda(\cdot ,q_1)\rVert_2 \lVert F_2\Psi_\lambda(\cdot ,q^{\prime}_1)\rVert_2 {\mathrm{d}} p {\mathrm{d}} p_1' {\mathrm{d}} q_1 {\mathrm{d}} q_1' \nonumber\\ & \leq \frac{\lambda^2}{2\pi^2}\lVert W \rVert_1\lVert V\rVert_1\Bigg[\sup_{q_1,q_1'\in {\mathbb{R}}}\int_{{\mathbb{R}}^3} B_{T_c^1}(p,(q_1,\eta))B_{T_c^1}((p^{\prime}_1,p_2),(q^{\prime}_1,\eta)) \chi_{p_1^{\prime\, 2}+q_1^{\prime\, 2}+p_2^2<2\mu}\chi_{p^2+q_1^2<2\mu} {\mathrm{d}} p {\mathrm{d}} p_1'\Bigg] \nonumber\\ &\qquad \times \Big( \int_{\mathbb{R}} \lVert F_2\Psi_\lambda(\cdot ,q_1)\rVert_2 \chi_{q_1^2<2\mu} {\mathrm{d}} q_1 \Big)^2. \end{align} $$

The integral over the product of the two $B_{T_c^1}$ terms is of order $O((\ln \mu /T_c^1(\lambda ))^3)$ by Lemma 3.7. Together with the asymptotics of $T_c^1(\lambda )$ in Remark 3.1, the term in the square bracket in equation (5.17) is thus of order $O(\lambda ^{-3})$ . Splitting the domain of integration into $|q_1|/\sqrt {\mu }\gtrless (T_c^1/\mu )^\beta $ for some $0< \beta <1$ and using the Schwarz inequality, we observe that

(5.18) $$ \begin{align} \int_{\mathbb{R}} \lVert F_2\Psi_\lambda(\cdot ,q_1)\rVert_2 \chi_{q_1^2< 2\mu} {\mathrm{d}} q_1 \leq (2\sqrt{\mu}(T_c^1/\mu)^\beta)^{1/2} \lVert \Psi_\lambda \rVert_2 +(2\sqrt{2\mu})^{1/2} \lVert F_2\Psi_\lambda \chi_{|q_1|/\sqrt{\mu}>(T_c^1/\mu)^\beta} \rVert_2. \end{align} $$

It was shown in Lemma 3.2(3) that $\lVert F_2\Psi _\lambda \chi _{|q_1|/\sqrt {\mu }>(T_c^1/\mu )^\beta } \rVert _2=O(\lambda ^{1/2})$ . With the asymptotics of $T_c^1(\lambda )$ in Remark 3.1, we have $(T_c^1/\mu )^{\beta /2}\leq O((\ln \mu /T_c^1)^{-1})=O(\lambda )$ . Thus,

$$\begin{align*}\Big( \int_{\mathbb{R}} \lVert F_2\Psi_\lambda(\cdot ,q_1)\rVert_2 \chi_{q_1^2<2\mu} {\mathrm{d}} q_1 \Big)^2=O(\lambda) \end{align*}$$

and equation (5.17) is of order $O(1)$ .

Asymptotics of second line in equation (5.15): Writing out the definition of $\Phi _\lambda ^{d,<}$ , we have

(5.19) $$ \begin{align} & \int_{{\mathbb{R}}^4}V(r)\overline{\Phi_\lambda^{d,<}(r_1,z_2,z_1)}\Phi_\lambda^{d,<}(r_1,-z_2,z_1)e^{-2i\eta(\lambda) r_2} {\mathrm{d}} r {\mathrm{d}} z =2\lambda^2\int_{{\mathbb{R}}^4}\widehat V(p_1+p_1',2\eta) B_{T_c^1}(p,(q_1,\eta)) \nonumber\\ & \times \overline{ \widehat{ V^{1/2}\Psi_\lambda}(p,q_1)}B_{T_c^1}((p_1',p_2),(q_1,\eta))\widehat{ V^{1/2}\Psi_\lambda}(p_1',p_2,q_1) \chi_{p^2+q_1^2<2\mu}\chi_{p_1^{\prime\, 2}+p_2^2+q_1^2<2\mu}{\mathrm{d}} p {\mathrm{d}} p_1' {\mathrm{d}} q_1. \end{align} $$

We can thus write

(5.20) $$ \begin{align} \frac{1}{2}\int_{{\mathbb{R}}^4}V(r)\overline{\Phi_\lambda^{<,d}(r_1,z_2,z_1)}\Big(\Phi_\lambda^{<,d}(r_1,z_2,z_1) +\Phi_\lambda^{<,d}(r_1,-z_2,z_1)e^{-2i\eta(\lambda) r_2}\Big) {\mathrm{d}} r {\mathrm{d}} z =\langle F_2 \Psi_\lambda, M_{\lambda} F_2 \Psi_\lambda \rangle , \end{align} $$

where $M_\lambda $ is the operator acting on $L^2({\mathbb {R}}^3)$ given by

(5.21) $$ \begin{align} \langle \psi, M_\lambda \psi \rangle= \lambda^2\int_{{\mathbb{R}}^4}& (\widehat V(p_1-p_1',0)+\widehat V(p_1+p_1',2\eta)) B_{T_c^1}(p,(q_1,\eta))\overline{ F_1 V^{1/2}\psi (p,q_1)} \chi_{p^2+q_1^2<2\mu} \nonumber\\ &\quad \times B_{T_c^1}((p_1',p_2),(q_1,\eta))\chi_{p_1^{\prime\, 2}+p_2^2+q_1^2<2\mu} F_1 V^{1/2}\psi (p_1',p_2,q_1){\mathrm{d}} p {\mathrm{d}} p_1' {\mathrm{d}} q_1. \end{align} $$

By the same argument as in the proof of $\int _{{\mathbb {R}}^4} V(r) \vert \Phi _\lambda ^{d,<}(r_1,z_2,z_1)\vert ^2 {\mathrm {d}} r {\mathrm {d}} z=O(\lambda ^{-1})$ in Lemma 3.5 (see equation (3.31)), we have $\lVert M_\lambda \rVert = O(\lambda ^{-1})$ . Recall the projections ${\mathbb {P}}$ and ${\mathbb {Q}}_\beta $ from Section 4. Let ${\mathbb {T}}$ be the projection ${\mathbb {T}}={\mathbb {P}} {\mathbb {Q}}_\beta $ for some $0<\beta <1$ and ${\mathbb {T}}^\perp =1-{\mathbb {T}}$ . We have

(5.22) $$ \begin{align} \langle F_2 \Psi_\lambda, M_\lambda F_2 \Psi_\lambda \rangle = \langle {\mathbb{T}} F_2 \Psi_\lambda, M_\lambda {\mathbb{T}} F_2 \Psi_\lambda \rangle + \langle {\mathbb{T}} F_2 \Psi_\lambda, M_\lambda {\mathbb{T}}^\perp F_2 \Psi_\lambda \rangle + \langle {\mathbb{T}}^\perp F_2 \Psi_\lambda, M_\lambda F_2 \Psi_\lambda \rangle. \end{align} $$

Since ${\mathbb {P}} $ and ${\mathbb {Q}}_\beta $ commute, we have $\lVert {\mathbb {T}}^\perp F_2 \Psi _\lambda \rVert =\lVert {\mathbb {Q}}_\beta ^\perp F_2\Psi _\lambda +{\mathbb {Q}}_\beta {\mathbb {P}}^\perp F_2 \Psi _\lambda \rVert =O(\lambda ^{1/2})$ according to the asymptotics for $\lVert {\mathbb {Q}}^\perp F_2 \Psi _\lambda \rVert $ and $\lVert {\mathbb {P}}^\perp F_2 \Psi _\lambda \rVert $ proved in Lemma 3.2(2) and equation (3). In particular, the last two terms in equation (5.22) are of order $O(\lambda ^{-1/2})$ . The remaining term in equation (5.22) is bounded below by

(5.23) $$ \begin{align} & \langle {\mathbb{T}} F_2 \Psi_\lambda, M_\lambda {\mathbb{T}} F_2 \Psi_\lambda \rangle \nonumber\\ & \geq \inf_{|q_1|/\sqrt{\mu}<(T_c^1/\mu)^\beta} \lambda^2\int_{{\mathbb{R}}^3}(\widehat V(p_1-p_1',0)+\widehat V(p_1+p_1',2\eta)) B_{T_c^1}((p_1,p_2),(q_1,\eta)) \widehat{ V j_2} (p) \chi_{p^2+q_1^2<2\mu} \nonumber\\ &\qquad \times B_{T_c^1}((p_1',p_2),(q_1,\eta))\chi_{p_1^{\prime\, 2}+p_2^2+q_1^2<2\mu}\widehat{Vj_2} (p_1',p_2){\mathrm{d}} p {\mathrm{d}} p_1' \lVert {\mathbb{T}} F_2 \Psi_\lambda \rVert_2^2\lVert V^{1/2}j_2\rVert_2^{-2}. \end{align} $$

The remainder of the proof follows the same ideas as the proof of [16, Lemma 4.11]. Since $V\geq 0$ , we have $\widehat {V}(0)>0$ . Furthermore, the eigenvalue equation $e_\mu V^{1/2}j_2=O_\mu V^{1/2}j_2=\widehat {Vj_2}(|p|=\sqrt {\mu }) V^{1/2}j_2 $ implies that $\widehat {Vj_2}(|p|=\sqrt {\mu })=e_\mu>0$ . By continuity of $\widehat {V}$ and $\widehat {Vj_2}$ and since $\eta (\lambda )\to 0$ for $\lambda \to 0$ (see Lemma 3.2(1)), there exist $\tilde \lambda>0$ , $0<\delta <\mu $ and $c_1>0$ such that for all $\sqrt {\mu -\delta }<p_2<\sqrt {\mu +\delta }, p_1^2<4\delta ,p_1^{\prime\, 2}<4 \delta $ and $\lambda <\tilde \lambda $ we have

(5.24) $$ \begin{align} (\widehat V(p_1-p_1',0)+\widehat V(p_1+p_1',2\eta)) \widehat{ Vj_2} (p) \widehat{Vj_2} (p_1',p_2)\chi_{p^2+q_1^2<2\mu}\chi_{p_1^{\prime\, 2}+p_2^2+q_1^2<2\mu}\lVert V^{1/2}j_2\rVert_2^{-2}>c_1. \end{align} $$

Using the second part of Lemma 3.7 and the boundedness of $\widehat {V}, \widehat {Vj_2}$ , it follows that up to an error of order $O(\lambda ^2 (\ln \mu /T_c^1)^{5/2})=O(\lambda ^{-1/2})$ we may restrict the domain of integration in equation (5.23) to $\sqrt {\mu -\delta }<p_2<\sqrt {\mu +\delta }, p_1^2<4\delta ,p_1^{\prime\, 2}<4 \delta $ . Since $\lVert {\mathbb {T}} F_2 \Psi _\lambda \rVert _2^2=1-O(\lambda ) \geq \frac {1}{2}$ for small $\lambda $ , we obtain

(5.25) $$ \begin{align} \langle {\mathbb{T}} F_2 \Psi_\lambda, M_\lambda {\mathbb{T}} F_2 \Psi_\lambda \rangle & \geq \frac{c_1}{2}\inf_{|q_1|/\sqrt{\mu}<(T_c^1/\mu)^\beta} \lambda^2\int_{{\mathbb{R}}^3} B_{T_c^1}((p_1,p_2),(q_1,\eta)) \nonumber\\ & \times B_{T_c^1}((p_1',p_2),(q_1,\eta))\chi_{\mu-\delta<p_2^2<\mu+\delta}\chi_{p_1^2<4 \delta} \chi_{p_1^{\prime\, 2}<4 \delta}{\mathrm{d}} p {\mathrm{d}} p_1' +O(\lambda^{-1/2}). \end{align} $$

Using Lemma 3.7 once more, we may leave away the characteristic functions at the expense of an error of order $O(\lambda ^{-1/2})$ . Since $\eta (\lambda )=O(T_c^1(\lambda ))$ , there is a $c_2>0$ such that $\eta ^2+(\sqrt {\mu }(T_c^1/\mu )^\beta )^2\leq c_2^2 \mu (T_c^1/\mu )^{2\beta }$ for $T_c^1<\mu $ . The following lemma, whose proof is given in Section 7.5, thus concludes the proof of Lemma 1.10.

Lemma 5.2. Let $\mu ,c_2>0$ , $0<\beta <1$ and $\epsilon :=c_2 \sqrt {\mu } (T/\mu )^{\beta }$ for $T>0$ . Then there are constants $T_0,C>0$ such that

(5.26) $$ \begin{align} \inf_{|q|<\epsilon} \int_{\mathbb{R}} \left(\int_{{\mathbb{R}}} B_{T}(p,q) {\mathrm{d}} p_1\right)^2{\mathrm{d}} p_2\geq C(\ln \mu/T)^3 \end{align} $$

for all $0<T<T_0$ .

6 Proof of Theorem 1.6

This section is dedicated to the proof of Theorem 1.6, which states that the relative difference of $T_c^2$ and $T_c^0$ vanishes in the weak coupling limit. It has been shown in [16, Theorem 1.7] that the relative difference of $T_c^1$ and $T_c^0$ vanishes in the weak coupling limit and we follow the same proof strategy here. We first switch to the Birman–Schwinger picture. Recall the Birman–Schwinger operator $A_T^0$ corresponding to $H_T^{\Omega _0}$ defined in equation (2.10). Furthermore, recall the notation $ t$ , $\tilde \Omega _2$ and the representation of $UH_T^{\Omega _2}U^\dagger $ in equation (4.2) from Section 5. The corresponding Birman–Schwinger operator $A_T^2:L^2_{\textrm {s}}(\tilde \Omega _2)\to L^2_{\textrm {s}}(\tilde \Omega _2)$ is given by

(6.1) $$ \begin{align} \langle \psi, A_T^2 \psi \rangle = \int_{{\mathbb{R}}^{4}}B_{T}(p,q) \left|\int_{\tilde\Omega_2}\frac{1}{(2\pi)^2} t (p_1,q_1,r_1,z_1) t (p_2,q_2,r_2,z_2) V^{1/2}(r)\psi(r,z) {\mathrm{d}} r {\mathrm{d}} z\right|^2{\mathrm{d}} p{\mathrm{d}} q, \end{align} $$

and it follows from the Birman–Schwinger principle that $\mathrm {sgn} \inf \sigma (H_T^{\Omega _2}) = \mathrm {sgn} (1/\lambda -\sup \sigma (A_T^{2}))$ . Let $a_T^j=\sup \sigma (A_T^j)$ . For $\lambda \to 0$ asymptotically $a_T^0=e_\mu \ln (\mu /T)+O(1)$ , see for example, [16, Section 6]. It is a straightforward generalization of [12, Lemma 4.1] that the claim (1.4) is equivalent to

(6.2) $$ \begin{align} \lim_{T\to0} (a_T^0-a_T^2)=0, \end{align} $$

and we refer to [12] for the proof.

To verify equation (6.2), the first step is to argue that $a_T^2\geq a_T^0$ for all $T>0$ . Lemma 1.1 together with [16, Lemma 2.3] imply that $\inf \sigma (H_T^{\Omega _2})\leq \inf \sigma (H_T^{\Omega _0})$ for all $\lambda ,T>0$ . Using the Birman–Schwinger principle, it follows that $a_T^2\geq a_T^0$ for all $T>0$ . For details, we refer to the proof of [16, Theorem 1.7].

It remains to show that $\lim _{T\to 0} (a_T^0-a_T^2)\geq 0$ . We decompose $A_T^2$ in the same spirit as we decomposed $A_T^1(q_2)$ in equation (2.16). For $A_T^1$ , the decomposition consisted of the ‘unperturbed’ term $A_T^0$ and the ‘perturbation term’ $G_T$ , where the first components of the momentum variables were swapped. For $A_T^2$ , we additionally get the terms arising from swapping the variables in the second component, which leads to four terms in total. Let $\tilde \iota : L^2(\tilde \Omega _2)\to L^2({\mathbb {R}}^{4})$ be the isometry

(6.3) $$ \begin{align} \tilde \iota \psi(r,z) = \frac{1}{2} \Big(\psi(r,z) \chi_{\tilde \Omega_2}& (r,z) +\psi(-r_1, r_2,-z_1,z_2) \chi_{\tilde \Omega_2}(-r_1,r_2,-z_1,z_2) \nonumber\\ & +\psi(r_1, -r_2,z_1,-z_2) \chi_{\tilde \Omega_2}(r_1,-r_2,z_1,-z_2)+\psi(-r,-z) \chi_{\tilde \Omega_2}(-r,-z) \Big). \end{align} $$

Using the definition of $ t$ and evenness of V in $r_1$ and $r_2$ , we rewrite equation (6.1) as

(6.4)

Define the self-adjoint operators $G_T^1, G_T^2$ and $N_T$ on $L^2({\mathbb {R}}^{4})$ through

(6.5) $$ \begin{align} \langle \psi, G_{T}^1\psi \rangle&=\int_{{\mathbb{R}}^{4}} \overline{F_1 V^{1/2}\psi((q_1,p_2),(p_1,q_2))} B_{T}(p,q) F_1 V^{1/2}\psi(p,q) {\mathrm{d}} p {\mathrm{d}} q, \end{align} $$

(6.6) $$ \begin{align} \langle \psi, G_{T}^2\psi \rangle&=\int_{{\mathbb{R}}^{4}} \overline{F_1 V^{1/2}\psi((p_1,q_2),(q_1,p_2))} B_{T}(p,q) F_1 V^{1/2}\psi(p,q) {\mathrm{d}} p {\mathrm{d}} q, \ \mathrm{and} \end{align} $$

(6.7) $$ \begin{align} \langle \psi, N_{T}\psi \rangle&=\int_{{\mathbb{R}}^{4}} \overline{F_1 V^{1/2}\psi(q,p)} B_{T}(p,q) F_1 V^{1/2}\psi(p,q) {\mathrm{d}} p {\mathrm{d}} q. \end{align} $$

We slightly abuse notation and write $F_2$ for the Fourier transform in the second variable also when the second variable has two components, that is, $F_2 \psi (r, q)=\frac {1}{2\pi } \int _{{\mathbb {R}}^2} e^{-iq \cdot z} \psi (r,z) {\mathrm {d}} z$ . It follows from equation (6.4) and $B_T(p,q)=B_T((q_1,p_2),(p_1,q_2))=B_T(q,p)$ that

(6.8) $$ \begin{align} A_T^2= \tilde \iota^\dagger (A_T^0- F_2^\dagger R_T F_2) \tilde \iota, \end{align} $$

where $R_T=\pm G_T^1 \pm G_T^2 - N_T$ . Let $B_T(\cdot ,q):L^2({\mathbb {R}}^2)\to L^2({\mathbb {R}}^2)$ denote multiplication by $B_T(p,q)$ in momentum space and define the function $E_T(q)$ on ${\mathbb {R}}^2$ through

(6.9) $$ \begin{align} E_T(q):=a_T^0-\lVert V^{1/2} B_T(\cdot,q) V^{1/2}\rVert_{\textrm{s}}, \end{align} $$

where $\lVert \cdot \rVert _{\textrm {s}}$ denotes the operator norm of the operator restricted to even functions. Note that $a_T^0=\sup _{q\in {\mathbb {R}}^2}\lVert V^{1/2} B_T(\cdot ,q) V^{1/2}\rVert _{\textrm {s}}$ and therefore $E_T(q)\geq 0$ . For $\psi \in L^2({\mathbb {R}}^4)$ , let $E_T \psi (r,q)=E_T(q) \psi (r,q)$ . We get the operator inequality $a_T^0 {\mathbb {I}} -A_T^0 \geq F_2^\dagger E_T F_2$ , where ${\mathbb {I}}$ denotes the identity operator on $L_{\textrm {s}}^2({\mathbb {R}}^4)$ . Using equation (6.8), the above inequality and that $\lVert F_2 \tilde \iota \psi \rVert _2=\lVert \psi \rVert _2$ we obtain

(6.10) $$ \begin{align} a_T^0-a_T^2 \geq \inf_{\psi \in L^2_s(\tilde \Omega_2), \lVert \psi\rVert_2=1} \langle F_2\tilde \iota \psi,( E_T +R_T) F_2 \tilde \iota \psi \rangle \geq \inf_{\psi \in L^2({\mathbb{R}}^4), \lVert \psi\rVert_2=1} \langle \psi,( E_T +R_T) \psi \rangle. \end{align} $$

Therefore, it suffices to show that $\lim _{T\to 0} \inf \sigma ( E_{T}+R_T)\geq 0$ . The proof relies on the following three lemmas.

Lemma 6.1. Let $\mu>0$ and let V satisfy Assumption 1.2. Then $\sup _{T>0} \lVert R_{T} \rVert <\infty $ .

Lemma 6.2. Let $\mu>0$ and let V satisfy Assumption 1.2. Let ${\mathbb {I}}_{\leq \epsilon }$ act on $L^2({\mathbb {R}}^{4})$ as ${\mathbb {I}}_{\leq \epsilon } \psi (r,q)=\psi (r,q)\chi _{\vert q\vert \leq \epsilon }$ . Then $\lim _{\epsilon \to 0} \sup _{T>0} \lVert {\mathbb {I}}_{\leq \epsilon } R_{T} {\mathbb {I}}_{\leq \epsilon } \lVert =0$ .

Lemma 6.3. Let $\mu>0$ and let V satisfy Assumption 1.2. Let $0<\epsilon <\sqrt {\mu }$ . There are constants $c_1,c_2,T_0>0$ such that for $0<T<T_0$ and $|q|>\epsilon $ we have $ E_{T}(q)>c_1 \vert \ln (c_2/T)\vert $ .

The first two lemmas are extensions of [16, Lemma 6.1 and Lemma 6.2] and proved in Sections 7.6 and 7.7, respectively. The third lemma is contained in [16, Lemma 6.3].

With these lemmas, the claim follows completely analogously to the proof of [12, Theorem 1.2 (ii)] and we provide a sketch for completeness. Using that $E_{T}(q)\geq 0$ , we write

(6.11) $$ \begin{align} E_{T}+ R_{T}+\delta=\sqrt{E_{T}+\delta}\left({\mathbb{I}} + \frac{1}{\sqrt{E_{T}+\delta}}R_{T}\frac{1}{\sqrt{E_{T}+\delta}}\right)\sqrt{E_{T}+\delta} \end{align} $$

for any $\delta>0$ . It suffices to prove that for all $\delta>0$ the norm of the second term in the bracket vanishes in the limit $T\to 0$ . With the notation from Lemma 6.2, we estimate for all $0<\epsilon <\sqrt {\mu }$

(6.12) $$ \begin{align} \left\lVert \frac{1}{\sqrt{E_{T}+\delta}}R_{T}\frac{1}{\sqrt{E_{T}+\delta}} \right\rVert & \leq \left\lVert {\mathbb{I}}_{\leq\epsilon} \frac{1}{\sqrt{E_{T}+\delta}}R_{T}\frac{1}{\sqrt{E_{T}+\delta}}{\mathbb{I}}_{\leq\epsilon}\right\rVert \nonumber\\ & \quad +\left\lVert {\mathbb{I}}_{\leq\epsilon} \frac{1}{\sqrt{E_{T}+\delta}}R_{T}\frac{1}{\sqrt{E_{T}+\delta}}{\mathbb{I}}_{>\epsilon}\right\rVert +\left\lVert {\mathbb{I}}_{>\epsilon} \frac{1}{\sqrt{E_{T}+\delta}}R_{T}\frac{1}{\sqrt{E_{T}+\delta}}\right\rVert\,. \end{align} $$

Lemma 6.3 and $E_{T}\geq 0$ imply

(6.13) $$ \begin{align} \lim_{T\to 0}\left\lVert \frac{1}{\sqrt{E_{T}+\delta}}R_{T}\frac{1}{\sqrt{E_{T}+\delta}}\right\rVert \leq \sup_{T>0} \frac{1}{\delta}\left\lVert {\mathbb{I}}_{\leq\epsilon} R_{T} {\mathbb{I}}_{\leq\epsilon}\right\rVert+\lim_{T\to 0} \frac{2}{(\delta c_1 \vert \ln(c_2/T)\vert)^{1/2}} \lVert R_{T} \rVert. \end{align} $$

The first term can be made arbitrarily small by Lemma 6.2, and the second term vanishes by Lemma 6.1. Hence, Theorem 1.6 follows.

7 Proofs of Auxiliary Lemmas

7.1 Proof of Lemma 2.2

Proof of Lemma 2.2

Using the Mittag–Leffler series (as in [12, (2.1)]), one can write

(7.1) $$ \begin{align} f(p,q,x) & =2T\sum_{n\in {\mathbb{Z}}} \Xi_n^{-1}\Big[(2q_2+ x ) (2\mu -2q^2-2p^2-x^2+2(p_2-q_2)x) \nonumber\\ &\quad +2p_2(4 p \cdot q- 2 i w_n+2(p_2-q_2)x -x^2)\Big], \end{align} $$

where

(7.2) $$ \begin{align} \Xi_n &=\left(\left(p+q+(0,x)\right)^2-\mu-iw_n\right) \left(\left(p-q-(0,x)\right)^2-\mu+iw_n\right) \nonumber\\ &\quad\times \left(\left(p+q\right)^2-\mu-iw_n\right)\left(\left(p-q\right)^2-\mu+iw_n\right) \end{align} $$

and $w_n=(2n+1)\pi T$ . Continuity of f follows from dominated convergence. For $x>\sqrt {\mu }/4$ , the bound on f follows from the bound on $B_T$ in (2.2). Let $Q_2=Q_1+\sqrt {\mu }/4$ . For $x<\sqrt {\mu }/4$ , we have

(7.3) $$ \begin{align} |f(p,q,x)|\leq \sup_{|q_2|\leq Q_2} |\frac{\partial}{\partial q_2} B_T(p,q)|=\sup_{|q_2|\leq Q_2}| f(p,q,0)|. \end{align} $$

To bound $| f(p,q,0)|$ , first note that for $x=0$ with the notation $y=(p+q)^2-\mu $ , $z=(p-q)^2-\mu $ and $v=\max \{\left (|p_1|+|q_1|\right )^2+(|p_2|-|q_2|)^2-\mu ,0\} $ ,

(7.4) $$ \begin{align} |\Xi_n| = \left(y^2+w_n^2\right)\left(z^2+w_n^2\right) \geq \left(v^2+w_n^2\right)\left(\max\{(|p_2|-|q_2|)^2-\mu,0\})^2+w_n^2\right). \end{align} $$

Furthermore,

(7.5) $$ \begin{align} & \sup_{(p,q)\in {\mathbb{R}}^{4}, \vert q_2 \vert\leq Q_2}\left \vert \frac{4 i w_n p_2}{\max\{(|p_2|-|q_2|)^2-\mu,0\})^2+w_n^2}\right \vert \nonumber\\ &\qquad\qquad\qquad\qquad\qquad \leq \sup_{(p,q)\in {\mathbb{R}}^{4}, \vert q_2 \vert<Q_2} \frac{ 4\vert p_2\vert }{\sqrt{\max\{(|p_2|-|q_2|)^2-\mu,0\})^2+w_0^2}}=:c_1 <\infty. \end{align} $$

There is a constant $c_2>\mu $ depending only on $\mu $ and $Q_2$ such that $|p_2|^2\leq 4(\min \{y,z\}+c_2)$ for $|q_2|\leq Q_2$ and all $p_1,q_1\in {\mathbb {R}}$ . One obtains that for $|q_2|\leq Q_2$

(7.6) $$ \begin{align} \vert f(p,q,0) \vert \leq 2T\sum_{n\in {\mathbb{Z}}} \frac{2Q_2|y+z|+4 \sqrt{\min\{y,z\}+c_2} |y-z|}{(y^2+w_n^2)(z^2+w_n^2)} + 2T\sum_{n\in {\mathbb{Z}}}\frac{c_1}{v^2+w_n^2}. \end{align} $$

Since the summands are decreasing in n, we can estimate the sums by integrals. The second term is bounded by

(7.7) $$ \begin{align} 4T c_1\left[ \frac{1}{v^2 +w_0^2} +\int_{1/2}^\infty \frac{1}{v^2+4\pi^2T^2 x^2} {\mathrm{d}} x \right] &=4T c_1 \left[ \frac{1}{v^2+w_0^2} +\frac{\arctan \left(\frac{v}{\pi T}\right)}{2\pi T v}\right] <\frac{C}{1+p_1^2+q_1^2+p_2^2} \end{align} $$

for some constant C independent of p and $q_1$ since $\sup _{(p,q)\in {\mathbb {R}}^{4}, \vert q_2 \vert \leq Q_2} \frac {1+p_1^2+q_1^2+p_2^2}{1+v}<\infty $ . The first term in equation (7.6) is bounded by

(7.8) $$ \begin{align} & 16T (Q_2+2 \sqrt{\min\{|y|,|z|\}+c_2} )\max\{|y|,|z|\} \Bigg[ \frac{1}{(y^2+w_0^2)(z^2+w_0^2)} \nonumber\\ &\quad +\int_{1/2}^\infty \frac{1}{(y^2+4\pi^2T^2 x^2)(z^2+4\pi^2T^2 x^2)}{\mathrm{d}} x \Bigg]. \end{align} $$

Note that $y+z+2\mu +1=1+2p^2+2q^2$ . The claim thus follows if we prove that for $c_3>0$

(7.9) $$ \begin{align} \sup_{y>z>0}(1+y+z)(1+\sqrt{z+1})y\Bigg[ \frac{1}{(y^2+1)(z^2+1)} +\int_{c_3}^\infty \frac{1}{(y^2+ x^2)(z^2+x^2)}{\mathrm{d}} x \Bigg]<\infty. \end{align} $$

The supremum over the first summand is obviously finite. The supremum over the second summand is bounded by

(7.10) $$ \begin{align} \sup_{y>z>0}\frac{(1+2y)y}{y^2+ c_3^2} \frac{1+\sqrt{z+1}}{(z^2+c_3^2)^{1/4}}\int_{c_3}^\infty \frac{1}{x^{3/2}}{\mathrm{d}} x <\infty. \end{align} $$

7.2 Proof of Lemma 3.7

Proof of Lemma 3.7

Using the inequality (3.22) and substituting $p_1 \pm q_1\to p_1, p_1'\pm q_1' \to p_1'$ , we have

(7.11) $$ \begin{align} \int_{{\mathbb{R}}^3} B_{T}(p,q) B_{T}((p^{\prime}_1,p_2),q')& {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2 \leq \frac{1}{4}\int_{{\mathbb{R}}^3}( B_{T}((p_1,p_2+q_2),0) +B_{T}((p_1,p_2-q_2),0) ) \nonumber\\ & \times(B_{T}((p^{\prime}_1,p_2+q_2'),0) +B_{T}((p^{\prime}_1,p_2-q_2'),0) ) {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2. \end{align} $$

One can bound this from above by

(7.12) $$ \begin{align} & \sup_{q_2,q_2'\in {\mathbb{R}}}\int_{{\mathbb{R}}} \left(\int_{\mathbb{R}} B_{T}((p_1,p_2+q_2),0){\mathrm{d}} p_1 \right) \left(\int_{\mathbb{R}} B_{T}((p^{\prime}_1,p_2+q_2'),0) {\mathrm{d}} p_1' \right){\mathrm{d}} p_2 \nonumber\\ &\quad \leq \sup_{q_2\in {\mathbb{R}}}\int_{{\mathbb{R}}^3}B_{T}((p_1,p_2+q_2),0) B_{T}((p^{\prime}_1,p_2+q_2),0) {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2 \nonumber\\ &\quad =\int_{{\mathbb{R}}^3}B_{T}((p_1,p_2),0) B_{T}((p^{\prime}_1,p_2),0) {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2, \end{align} $$

where in the second step we used the Schwarz inequality in $p_2$ . The latter expression is of order $O(\ln (\mu /T)^3)$ for $T\to 0$ , as was shown in the proof of [16, Lemma 4.10].

To prove the second statement, we shall use that for fixed $0<\delta <\mu $

(7.13) $$ \begin{align} \int_{{\mathbb{R}}^3}(1-\chi_{\mu-\delta<p_2^2<\mu}\chi_{p_1^2<2\delta}\chi_{p_1^{\prime\, 2}<2\delta}) B_{T}(p,0) B_{T}((p^{\prime}_1,p_2),0) {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2 = O((\ln \mu/T)^2) \end{align} $$

for $T\to 0$ as was shown in the proof of [16, Lemma 4.10]. We choose $\delta _2$ and $\delta $ small enough such that for all $q^2<\delta _2$ , if $ p_1^2>4\delta _1$ we have $(p_1+q_1)^2>2\delta $ and if $p_2^2<\mu -\delta _1$ or $p_2^2>\mu +\delta _1$ we have $(p_2+q_2)^2<\mu -\delta $ or $(p_2+q_2)^2>\mu $ , respectively. Using the same inequality (3.22) as above, we have

(7.14) $$ \begin{align} & \sup_{q^2,q^{\prime\, 2}<\delta_2}\int_{{\mathbb{R}}^3}(1-\chi_{\mu-\delta_1<p_2^2<\mu+\delta_1}\chi_{p_1^2<4\delta_1}\chi_{p_1^{\prime\, 2}<4\delta_1}) B_{T}(p,q) B_{T}((p^{\prime}_1,p_2),q') {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2 \nonumber\\ & \leq \sup_{q^2,q^{\prime\, 2}<\delta_2}\int_{{\mathbb{R}}^3}(1-\chi_{\mu-\delta_1<p_2^2<\mu+\delta_1}\chi_{p_1^2<4\delta_1}\chi_{p_1^{\prime\, 2}<4\delta_1}) B_{T}(p+q,0) B_{T}((p^{\prime}_1,p_2)+q',0) {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2. \end{align} $$

Note that $1-\chi _{\mu -\delta _1<p_2^2<\mu +\delta _1}\chi _{p_1^2<4\delta _1}\chi _{p_1^{\prime\, 2}<4\delta _1} \leq \chi _{\mu -\delta _1>p_2^2}+ \chi _{\mu +\delta _1<p_2^2}+ \chi _{p_1^2>4\delta _1}+ \chi _{p_1^{\prime\, 2}>4\delta _1}$ . Using the Schwarz inequality in $p_2$ we bound equation (7.15) above by

(7.15) $$ \begin{align} &\quad \sup_{q^2<\delta_2}\int_{{\mathbb{R}}^3}( \chi_{\mu-\delta_1>p_2^2}+ \chi_{\mu+\delta_1<p_2^2}) B_{T}(( p_1+q_1, p_2+q_2),0) B_{T}(( p^{\prime}_1+q_1, p_2+q_2),0) {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2 \nonumber\\ & + 2 \sup_{q^2,q^{\prime\, 2}<\delta_2} \Big(\int_{{\mathbb{R}}^3} B_T((p_1+q_1,p_2+q_2),0) B_T((p_1'+q_1,p_2+q_2),0)\chi_{p_1^2>4\delta_1}\chi_{p_1^{\prime\, 2}>4\delta_1}{\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2\Big)^{1/2} \nonumber\\ &\qquad\qquad \times\Big(\int_{{\mathbb{R}}^3} B_T((p_1,p_2+q_2),0) B_T((p_1',p_2+q_2),0){\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2\Big)^{1/2}. \end{align} $$

Substituting $p_j+q_j\to p_j$ and by choice of $\delta _2$ and $\delta $ , this is bounded above by

(7.16) $$ \begin{align} & \int_{{\mathbb{R}}^3}( \chi_{\mu-\delta>p_2^2}+ \chi_{\mu<p_2^2}) B_{T}(p,0) B_{T}(( p^{\prime}_1, p_2),0) {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2 \nonumber\\ &\qquad + 2 \Big(\int_{{\mathbb{R}}^3} B_T(p,0) B_T((p_1',p_2),0)\chi_{p_1^2>2\delta}\chi_{p_1^{\prime\, 2}>2\delta}{\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2\Big)^{1/2} \nonumber\\ & \qquad \times\Big(\int_{{\mathbb{R}}^3} B_T(p,0) B_T((p_1',p_2),0){\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} p_2\Big)^{1/2}. \end{align} $$

By equation (7.14) and the first part of this lemma, this is of order $O((\ln \mu /T)^2)+O((\ln \mu /T)(\ln \mu /T)^{3/2})=O((\ln \mu /T)^{5/2})$ .

7.3 Proof of Lemma 3.8

Proof of Lemma 3.8

For $p_2,q_2\in {\mathbb {R}}$ let $B_{T}((\cdot ,p_2),(\cdot ,q_2)) $ , denote the self-adjoint operator on $L^2((-\sqrt {2\mu },\sqrt {2\mu }))$ acting as $\langle \psi ,B_{T}((\cdot ,p_2),(\cdot ,q_2)) \psi \rangle = \int _{-\sqrt {2\mu }}^{\sqrt {2\mu }}\int _{-\sqrt {2\mu }}^{\sqrt {2\mu }}\overline {\psi (p_1)}B_T(p,q) \psi (q_1) {\mathrm {d}} p_1{\mathrm {d}} q_1$ . Enlarging the domain of integration for $(q_1,p_2)$ from a disk to square, we have

(7.17) $$ \begin{align} \lVert B_{T}^{{ ex}, 2}(\xi) \rVert &\leq \sup_{\lVert \psi \rVert_2=1} \int_{(-\sqrt{2\mu},\sqrt{2\mu})^4} \overline{\psi(p_1')}B_{T} ((p_1',p_2),(q_1,\xi)) B_{T}(p,(q_1,\xi))\psi(p_1) {\mathrm{d}} p_1 {\mathrm{d}} p_1' {\mathrm{d}} q_1 {\mathrm{d}} p_2 \nonumber \\ & = \sup_{\lVert \psi \rVert_2=1} \int_{-\sqrt{2\mu}}^{\sqrt{2\mu}}\langle \psi, B_{T}((\cdot,p_2),(\cdot,\xi)) ^2\psi \rangle {\mathrm{d}} p_2. \end{align} $$

By the triangle inequality,

(7.18) $$ \begin{align} \lVert B_{T}^{{ ex}, 2}(\xi) \rVert\leq \int_{-\sqrt{2\mu}}^{\sqrt{2\mu}}\lVert B_{T}((\cdot,\xi),(\cdot,p_2)) \rVert^2 {\mathrm{d}} p_2. \end{align} $$

For fixed $p_2,q_2$ , we derive two bounds on $\lVert B_{T}((\cdot ,p_2),(\cdot ,q_2)) \rVert ^2$ . For the first bound, we estimate the Hilbert–Schmidt norm using the bounds on $B_T$ (2.2):

(7.19) $$ \begin{align} \lVert B_{T}((\cdot,p_2),(\cdot,q_2)) \rVert^2 &\leq \lVert B_{T,\mu}((\cdot,p_2),(\cdot,q_2)) \rVert_{\mathrm{HS}}^2 \nonumber\\ & \leq \int_{-\sqrt{2\mu}}^{\sqrt{2\mu}}\int_{-\sqrt{2\mu}}^{\sqrt{2\mu}}\frac{1}{\max\{|p_1^2+q_1^2+p_2^2+q_2^2-\mu|^2,T^2\}} {\mathrm{d}} p_1 {\mathrm{d}} q_1 \nonumber\\ & \leq 2\pi \int_0^{2\sqrt{\mu}} \frac{r}{\max\{|r^2+p_2^2+q_2^2-\mu|^2,T^2\}} {\mathrm{d}} r \leq \pi \int_{\mathbb{R}} \frac{1}{\max\{x^2,T^2\}} {\mathrm{d}} x=\frac{4\pi}{T}, \end{align} $$

where we first switched to angular coordinates and then substituted $x=r^2+p_2^2+q_2^2-\mu $ .

For the second bound, the idea is to apply [16, Lemma 6.5]. For $\mu _1,\mu _2\in {\mathbb {R}}$ , let $D_{\mu _1,\mu _2}$ be the operator on $L^2({\mathbb {R}})$ with integral kernel

(7.20) $$ \begin{align} D_{\mu_1,\mu_2}(p_1,q_1)=\frac{2}{|(p_1+q_1)^2-\mu_1|+|(p_1-q_1)^2-\mu_2|}. \end{align} $$

It was shown in [12, Lemma 4.6] that

(7.21) $$ \begin{align} B_T(p,q)\leq \frac{2}{|(p+q)^2-\mu|+|(p-q)^2-\mu|}. \end{align} $$

In particular, we have $\lVert B_{T}((\cdot ,p_2),(\cdot ,q_2)) \rVert \leq \lVert D_{\mu -(p_2+q_2)^2,\mu -(p_2-q_2)^2}\rVert $ and

(7.22) $$ \begin{align} \lVert B_T^{{ ex},2}(\xi) \rVert \leq \int_{-\sqrt{2\mu}}^{\sqrt{2\mu}}\min\Big\{ \frac{4\pi}{T},\lVert D_{\mu-(\xi+q_2)^2,\mu-(\xi-q_2)^2}\rVert ^2\Big\} {\mathrm{d}} q_2. \end{align} $$

According to [16, Lemma 6.5], for $\mu _1,\mu _2\leq \mu $ there is a constant $C>0$ such that

(7.23) $$ \begin{align} \lVert D_{\mu_1,\mu_2} \rVert \leq C+\frac{C \mu^{1/2}}{|\min\{\mu_1,\mu_2\}|^{1/2}}\Bigg[1+\chi_{\min\{\mu_1,\mu_2\}<0<\max\{\mu_1,\mu_2\} }\ln \left(1+\frac{\max\{\mu_1,\mu_2\}}{\vert \min\{\mu_1,\mu_2\}\vert}\right)\Bigg]. \end{align} $$

The condition $\mu -(|q_2|+|\xi |)^2<0<\mu -(|q_2|-|\xi |)^2 $ can only be satisfied for $\sqrt {\mu }-|\xi | \leq |q_2|\leq \sqrt {\mu }+|\xi |$ . We get the bound

(7.24) $$ \begin{align} \sup_{|\xi|<cT} \lVert B_T^{{ ex},2}(\xi) \rVert & \leq C \Bigg(\int_{||q_2|-\sqrt{\mu}|<2cT}\frac{1}{T} {\mathrm{d}} q_2 \nonumber\\ & \quad + \sup_{|\xi|<cT}\int_{-\sqrt{2\mu}}^{\sqrt{2\mu}} \chi_{||q_2|-\sqrt{\mu}|>2cT}\left[1+\frac{1}{|\mu-(|q_2|+|\xi|)^2|^{1/2}}\right]^2{\mathrm{d}} q_2\Bigg) \leq \tilde C(1+\ln \mu/T). \end{align} $$

7.4 Proof of Lemma 5.1

Proof of Lemma 5.1

Applying the inequality (3.22), we have

(7.25) $$ \begin{align} &\sup_{q_1}\int_{{\mathbb{R}}} B_{T,\mu}((p_1,\xi(T)),(q_1,\xi'(T))){\mathrm{d}} p_1 \nonumber\\ &\quad \leq \frac{1}{2} \left[\int_{{\mathbb{R}}} B_{T,\mu}((p_1,\xi(T)+\xi'(T)),0){\mathrm{d}} p_1 +\int_{{\mathbb{R}}} B_{T,\mu}((p_1,\xi(T)-\xi'(T)),0){\mathrm{d}} p_1\right]. \end{align} $$

The first integral equals

(7.26) $$ \begin{align} \int_{{\mathbb{R}}} B_{T,\mu-(\xi(T)+ \xi'(T))^2}(p_1,0){\mathrm{d}} p_1, \end{align} $$

where here $B_{T,\mu }$ is understood as the function defined through the same expression as $B_T$ in equation (2.1) on ${\mathbb {R}}\times {\mathbb {R}}$ instead of ${\mathbb {R}}^2\times {\mathbb {R}}^2$ . For the second integral, replace $ \xi '(T)$ by $- \xi '(T)$ . The claim follows from the asymptotics

(7.27) $$ \begin{align} \int_{{\mathbb{R}}} B_{T,\mu}(p_1,0){\mathrm{d}} p_1= \frac{2}{\sqrt{\mu}}(\ln(\mu/T)+O(1)) \end{align} $$

for $T/\mu \to 0$ ; see, for example, [12, Lemma 3.5].

7.5 Proof of Lemma 5.2

Proof of Lemma 5.2

Let $\gamma =\mu (T/\mu )^{\beta /2}$ . By invariance of $B_T(p,q)$ under $(p_j,q_j)\to -(p_j,q_j) $ for $j\in \{1,2\}$ , we may assume without loss of generality that $q\in [0,\infty )^2$ . For a lower bound, we restrict the integration to $p_1,p_2>0$ , $p_2^2<\mu -\epsilon ^2-\gamma $ and $p_1^2>(\sqrt {\mu }+\epsilon )^2+T-p_2^2$ . For $p,q\in [0,\infty )^2$ with $|q|<\epsilon $ and $p^2>(\sqrt {\mu }+\epsilon )^2+T$ , we have $(p-q)^2-\mu \geq ||p|-|q||^2-\mu \geq 0$ and $(p+q)^2-\mu \geq p^2+q^2-\mu \geq T$ . Therefore, in this regime

(7.28) $$ \begin{align} B_T(p,q)\geq \frac{1}{2}\frac{\tanh(1/2)}{p^2+q^2-\mu}. \end{align} $$

This is minimal if $|q|=\epsilon $ . Since for $a>b>0$

$$\begin{align*}\int_a^\infty \frac{1}{p_1^2-b^2} {\mathrm{d}} p_1=\frac{\operatorname{\mathrm{artanh}}(b/a)}{b}=\frac{1}{b}\operatorname{\mathrm{artanh}}\left(\sqrt{1-(a^2-b^2)/a^2}\right), \end{align*}$$

the left-hand side of equation (5.26) is bounded below by

(7.29) $$ \begin{align} \frac{\tanh(1/2)^2}{4}\int_{\sqrt{\mu-\delta}}^{\sqrt{\mu-\epsilon^2-\gamma}} \frac{\operatorname{\mathrm{artanh}}\left(\sqrt{1-\frac{2\sqrt{\mu}\epsilon+2\epsilon^2+T}{(\sqrt{\mu}+\epsilon)^2+T-p_2^2}}\right)^2}{\mu-\epsilon^2-p_2^2}{\mathrm{d}} p_2. \end{align} $$

By monotonicity of $\operatorname {\mathrm {artanh}}$ , the $\operatorname {\mathrm {artanh}}$ term in the integrand is minimal for $p_2=\sqrt {\mu -\epsilon ^2-\gamma }$ . Since $\int _{\sqrt {\mu -\delta }}^{\sqrt {\mu -\epsilon ^2-\gamma }} \frac {1}{\mu -\epsilon ^2-p_2^2}{\mathrm {d}} p_2=\frac {1}{\mu -\epsilon ^2}(\operatorname {\mathrm {artanh}}(\sqrt {1-(\epsilon ^2+\gamma )/\mu })-\operatorname {\mathrm {artanh}}(\sqrt {1-\delta /\mu }))$ , the left-hand side of equation (5.26) is bounded below by

(7.30) $$ \begin{align} \frac{\tanh(1/2)^2}{4(\mu-\epsilon^2)} \operatorname{\mathrm{artanh}}\left(\sqrt{1-\frac{2\sqrt{\mu}\epsilon+2\epsilon^2+T}{2\sqrt{\mu}\epsilon+2\epsilon^2+T+\gamma}}\right)^2\Bigg[\operatorname{\mathrm{artanh}}\left(\sqrt{1-\frac{\epsilon^2+\gamma}{\mu}}\right)-\operatorname{\mathrm{artanh}}\left(\sqrt{1-\frac{\delta}{\mu}}\right)\Bigg]. \end{align} $$

With $\operatorname {\mathrm {artanh}}(\sqrt {1-x})=\frac {1}{2}\ln (4/x)+o(1)$ as $x\to 0$ , we have for $T\to 0$

(7.31) $$ \begin{align} \operatorname{\mathrm{artanh}}\left(\sqrt{1-\frac{2\sqrt{\mu}\epsilon+2\epsilon^2+T}{2\sqrt{\mu}\epsilon+2\epsilon^2+T+\gamma}}\right)=\frac{\beta}{4}\ln(\mu/T)+O(1) \end{align} $$

and

(7.32) $$ \begin{align} \operatorname{\mathrm{artanh}}\left(\sqrt{1-\frac{\epsilon^2+\gamma}{\mu}}\right)=\frac{\beta}{4}\ln(\mu/T)+O(1). \end{align} $$

Hence, the left-hand side of equation (5.26) is bounded below by $\frac {\tanh (1/2)^2}{4^3}\frac { \beta ^3}{\mu }(\ln \mu /T)^3+O(\ln \mu /T)^2$ , and the claim follows.

7.6 Proof of Lemma 6.1

Proof of Lemma 6.1

According to [16, Lemma 6.1], $\sup _T\lVert G_T^j\rVert <\infty $ for $j\in \{1,2\}$ and it suffices to prove $\sup _T\lVert N_T\rVert <\infty $ . We have $\lVert N_T \rVert \leq \lVert N_T^<\rVert + \lVert N_T^>\rVert $ , where

(7.33) $$ \begin{align} \langle \psi, N_{T}^<\psi \rangle=\int_{{\mathbb{R}}^{4}} \overline{F_1 V^{1/2}\psi(q,p)} B_{T}(p,q)\chi_{p^2,q^2<2\mu} F_1 V^{1/2}\psi(p,q) {\mathrm{d}} p {\mathrm{d}} q \end{align} $$

and for $N_T^>$ replace the characteristic function by $1-\chi _{p^2,q^2<2\mu }$ .

To bound $\lVert N_T^> \rVert $ , we first use the Schwarz inequality to obtain

(7.34) $$ \begin{align} \lVert N_T^> \rVert \leq \sup_{\psi \in L^2({\mathbb{R}}^4), \lVert \psi\rVert_2=1} \int_{{\mathbb{R}}^{4}}B_{T}(p,q)(1-\chi_{p^2,q^2<2\mu}) |F_1 V^{1/2}\psi(p,q)|^2 {\mathrm{d}} p {\mathrm{d}} q. \end{align} $$

By the bound on $B_T$ in equation (2.2), there is a constant $C>0$ independent of T such that $\lVert N_T^> \rVert \leq C \lVert M \rVert $ , where $M:=V^{1/2} \frac {1}{1-\Delta } V^{1/2}$ on $L^2({\mathbb {R}}^2)$ . The Young and Hölder inequalities imply that M is a bounded operator [15].

To bound $\lVert N_T^< \rVert $ , we use that $\lVert F_1 V^{1/2} \psi ( \cdot ,q)\rVert _\infty \leq \lVert V\rVert _1^{1/2} \lVert \psi (\cdot ,q)\rVert _2$ by the Schwarz inequality and the upper bound for $B_T$ in (7.22) to obtain

(7.35) $$ \begin{align} \langle \psi, N_T^< \psi \rangle \leq 2 \lVert V \rVert_1 \int_{{\mathbb{R}}^4} \frac{\lVert \psi(\cdot,q)\rVert_2 \lVert \psi(\cdot,p)\rVert_2 }{|(p+q)^2-\mu|+|(p-q)^2-\mu|}\chi_{p^2,q^2<2\mu} {\mathrm{d}} p {\mathrm{d}} q. \end{align} $$

Recalling the definition of the operator $D_{\mu _1,\mu _2}$ from (7.21), this is further bounded by

(7.36) $$ \begin{align} 2 \lVert V \rVert_1 \int_{{\mathbb{R}}^2}\lVert \psi(\cdot,(\cdot, q_2))\rVert_2 \lVert D_{\mu-(p_2+q_2)^2,\mu-(p_2-q_2)^2} \rVert \lVert \psi(\cdot,(\cdot,p_2))\rVert_2 \chi_{p_2^2,q_2^2<2\mu} {\mathrm{d}} p {\mathrm{d}} q. \end{align} $$

It follows from the bound on $\lVert D_{\mu _1,\mu _2}\rVert $ in equation (7.24) that for any $\alpha>0$ there is a constant $C_\alpha $ independent of $p_2,q_2$ such that

$$\begin{align*}\lVert D_{\mu-(p_2+q_2)^2,\mu-(p_2-q_2)^2} \rVert \leq C_\alpha (1+|\mu-(|p_2|+|q_2|)^2|^{-1/2-\alpha}). \end{align*}$$

Let $\tilde D_\alpha $ denote the operator on $L^2((-\sqrt {2\mu },\sqrt {2\mu }))$ with integral kernel

$$\begin{align*}\tilde D_\alpha(q_2,p_2)=(1+|\mu-(|p_2|+|q_2|)^2|^{-1/2-\alpha}). \end{align*}$$

Then we have $\lVert N_T^<\rVert \leq 2 C_\alpha \lVert V\rVert _1 \lVert \tilde D_\alpha \rVert $ , and it remains to prove that $\lVert \tilde D_\alpha \rVert <\infty $ for a suitable choice of $\alpha $ . Applying the Schur test with constant test function gives

(7.37) $$ \begin{align} \lVert \tilde D_\alpha\rVert\leq \sup_{|q_2|<\sqrt{2\mu}} \int_{-\sqrt{2\mu}}^{\sqrt{2\mu}}(1+|\mu-(|p_2|+|q_2|)^2|^{-1/2-\alpha}) {\mathrm{d}} p_2, \end{align} $$

which is finite for $\alpha <1/2$ .

7.7 Proof of Lemma 6.2

Proof of Lemma 6.2

It was shown in [16, Lemma 6.2] that $\lim _{\epsilon \to 0} \sup _{T>0} \lVert {\mathbb {I}}_{\leq \epsilon } G_{T}^j {\mathbb {I}}_{\leq \epsilon } \lVert =0$ for $j\in \{1,2\}$ , and it remains to prove $\lim _{\epsilon \to 0} \sup _{T>0} \lVert {\mathbb {I}}_{\leq \epsilon } N_{T} {\mathbb {I}}_{\leq \epsilon } \lVert =0$ . We use the Schwarz inequality twice to bound

(7.38) $$ \begin{align} & \lVert {\mathbb{I}}_{\leq \epsilon} N_{T} {\mathbb{I}}_{\leq \epsilon} \lVert \leq \lVert V\rVert_1\sup_{\psi \in L^2({\mathbb{R}}^4), \lVert \psi\rVert_2=1} \int_{{\mathbb{R}}^4} \lVert \psi(\cdot,p)\rVert_2 B_T(p,q) \chi_{\vert p\vert,\vert q \vert\leq \epsilon} \lVert \psi(\cdot,q)\rVert_2 {\mathrm{d}} p {\mathrm{d}} q \nonumber\\ & \leq \lVert V\rVert_1 \sup_{\psi \in L^2({\mathbb{R}}^4), \lVert \psi\rVert_2=1} \int_{{\mathbb{R}}^4} B_T(p,q) \chi_{\vert p\vert,\vert q \vert\leq \epsilon} \lVert \psi(\cdot,q)\rVert_2^2 {\mathrm{d}} p {\mathrm{d}} q \leq \lVert V\rVert_1 \sup_{|q|\leq \epsilon} \int_{\vert p\vert\leq \epsilon} B_T(p,q){\mathrm{d}} p. \end{align} $$

Applying the bound on $B_T$ in equation (2.2), for $\epsilon <\sqrt {\mu /2}$ one can bound the right-hand side uniformly in T by

(7.39) $$ \begin{align} \lVert V\rVert_1 \sup_{|q|\leq \epsilon}\int_{\vert p\vert\leq \epsilon} \frac{1}{\mu-p^2-q^2} {\mathrm{d}} p, \end{align} $$

which vanishes as $\epsilon \to 0$ . The claim follows.