Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-06T15:44:53.251Z Has data issue: false hasContentIssue false
  • English
  • Français

VALUE PATTERNS OF MULTIPLICATIVE FUNCTIONS AND RELATED SEQUENCES

Part of: Ergodic theory Multiplicative number theory

Published online by Cambridge University Press:  26 September 2019

TERENCE TAO  and
JONI TERÄVÄINEN
TERENCE TAO
Affiliation:
Department of Mathematics, UCLA, 405 Hilgard Ave, Los Angeles CA 90095, USA; [email protected]
JONI TERÄVÄINEN
Affiliation:
Mathematical Institute, University of Oxford, Radcliffe Observatory Quarter, Woodstock Rd, Oxford OX2 6GG, UK; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the existence of various sign and value patterns in sequences defined by multiplicative functions or related objects. For any set 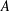$A$ whose indicator function is ‘approximately multiplicative’ and uniformly distributed on short intervals in a suitable sense, we show that the density of the pattern $n+1\in A$, $n+2\in A$, 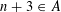$n+3\in A$ is positive as long as 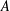$A$ has density greater than $\frac{1}{3}$. Using an inverse theorem for sumsets and some tools from ergodic theory, we also provide a theorem that deals with the critical case of 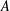$A$ having density exactly $\frac{1}{3}$, below which one would need nontrivial information on the local distribution of 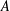$A$ in Bohr sets to proceed. We apply our results first to answer in a stronger form a question of Erdős and Pomerance on the relative orderings of the largest prime factors 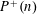$P^{+}(n)$, 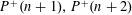$P^{+}(n+1),P^{+}(n+2)$ of three consecutive integers. Second, we show that the tuple 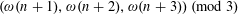$(\unicode[STIX]{x1D714}(n+1),\unicode[STIX]{x1D714}(n+2),\unicode[STIX]{x1D714}(n+3))~(\text{mod}~3)$ takes all the 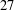$27$ possible patterns in 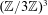$(\mathbb{Z}/3\mathbb{Z})^{3}$ with positive lower density, with $\unicode[STIX]{x1D714}(n)$ being the number of distinct prime divisors. We also prove a theorem concerning longer patterns $n+i\in A_{i}$, 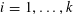$i=1,\ldots ,k$ in approximately multiplicative sets 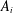$A_{i}$ having large enough densities, generalizing some results of Hildebrand on his ‘stable sets conjecture’. Finally, we consider the sign patterns of the Liouville function 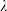$\unicode[STIX]{x1D706}$ and show that there are at least 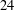$24$ patterns of length 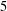$5$ that occur with positive upper density. In all the proofs, we make extensive use of recent ideas concerning correlations of multiplicative functions.

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Secondary: 37A45: Relations with number theory and harmonic analysis
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e33
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Balog, A., ‘Problem in ‘Tagunsbericht 41/1982”, Math. Forschungsinstitut Oberwolfach. 1982. p. 29.Google Scholar
Balog, A., ‘On triplets with descending largest prime factors’, Studia Sci. Math. Hungar. 38 (2001), 45–50.Google Scholar
Balog, A. and Wooley, T. D., ‘On strings of consecutive integers with no large prime factors’, J. Austral. Math. Soc. Ser. A 64(2) (1998), 266–276.Google Scholar
Chowla, S., The Riemann Hypothesis and Hilbert’s Tenth Problem, Mathematics and Its Applications, 4 (Gordon and Breach Science Publishers, New York–London–Paris, 1965).Google Scholar
Christ, M. and Iliopoulou, M., ‘Inequalities of Riesz–Sobolev type for compact connected Abelian groups’, Preprint, 2018.Google Scholar
De Koninck, J.-M. and Doyon, N., ‘On the distance between smooth numbers’, Integers 11(A25) (2011), 22.Google Scholar
de la Bretèche, R., Pomerance, C. and Tenenbaum, G., ‘Products of ratios of consecutive integers’, Ramanujan J. 9(1–2) (2005), 131–138.Google Scholar
Dickman, K., ‘On the frequency of numbers containing prime factors of a certain relative magnitude’, Ark. Mat. 22A(10) (1930), 1–14.Google Scholar
Elliott, P. D. T. A., ‘On the correlation of multiplicative and the sum of additive arithmetic functions’, Mem. Amer. Math. Soc. 112(538) (1994), viii+88.Google Scholar
Erdős, P., ‘Some unconventional problems in number theory’, inJournées Arithmétiques de Luminy (Colloq. Internat. CNRS, Centre Univ. Luminy, Luminy, 1978), Astérisque, 61 (Soc. Math. France, Paris, 1979), 73–82.Google Scholar
Erdős, P. and Pomerance, C., ‘On the largest prime factors of n and n + 1’, Aequationes Math. 17(2–3) (1978), 311–321.Google Scholar
Frantzikinakis, N. and Host, B., ‘Furstenberg systems of bounded multiplicative functions and applications’, Int. Math. Res. Not. IMRN to appear.Google Scholar
Frantzikinakis, N. and Host, B., ‘The logarithmic Sarnak conjecture for ergodic weights’, Ann. of Math. (2) 187(3) (2018), 869–931.Google Scholar
Frantzikinakis, N., Host, B. and Kra, B., ‘Multiple recurrence and convergence for sequences related to the prime numbers’, J. Reine Angew. Math. 611 (2007), 131–144.Google Scholar
Furstenberg, H., ‘Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions’, J. Anal. Math. 31 (1977), 204–256.Google Scholar
Furstenberg, H. and Weiss, B., ‘A mean ergodic theorem for (1/N)∑n=1 N f (T n x)g (T n 2 x)’, inConvergence in Ergodic Theory and Probability (Columbus, OH, 1993), Ohio State Univ. Math. Res. Inst. Publ., 5 (de Gruyter, Berlin, 1996), 193–227.Google Scholar
Glasner, E., Ergodic Theory via Joinings, Mathematical Surveys and Monographs, 101 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Green, B. and Tao, T., ‘Linear equations in primes’, Ann. of Math. (2) 171(3) (2010), 1753–1850.Google Scholar
Green, B. and Tao, T., ‘The Möbius function is strongly orthogonal to nilsequences’, Ann. of Math. (2) 175(2) (2012), 541–566.Google Scholar
Green, B., Tao, T. and Ziegler, T., ‘An inverse theorem for the Gowers U s+1[N]-norm’, Ann. of Math. (2) 176(2) (2012), 1231–1372.Google Scholar
Griesmer, J. T., ‘Semicontinuity of structure for small sumsets in compact abelian groups’, Preprint, 2018.Google Scholar
Hildebrand, A., ‘On a conjecture of Balog’, Proc. Amer. Math. Soc. 95(4) (1985), 517–523.Google Scholar
Hildebrand, A., ‘On consecutive values of the Liouville function’, Enseign. Math. (2) 32(3–4) (1986), 219–226.Google Scholar
Hildebrand, A., ‘On integer sets containing strings of consecutive integers’, Mathematika 36(1) (1989), 60–70.Google Scholar
Hildebrand, A., ‘Multiplicative properties of consecutive integers’, inAnalytic Number Theory (Kyoto, 1996), London Math. Soc. Lecture Note Ser., 247 (Cambridge Univ. Press, Cambridge, 1997), 103–117.Google Scholar
Hildebrand, A. and Tenenbaum, G., ‘Integers without large prime factors’, J. Théor. Nombres Bordeaux 5(2) (1993), 411–484.Google Scholar
Host, B. and Kra, B., ‘Nonconventional ergodic averages and nilmanifolds’, Ann. of Math. (2) 161(1) (2005), 397–488.Google Scholar
Klurman, O. and Mangerel, A. P., ‘Effective asymptotic formulae for multilinear averages of multiplicative functions’. Preprint, August 2017.Google Scholar
Matomäki, K. and Radziwiłł, M., ‘Multiplicative functions in short intervals’, Ann. of Math. (2) 183(3) (2016), 1015–1056.Google Scholar
Matomäki, K., Radziwiłł, M. and Tao, T., ‘An averaged form of Chowla’s conjecture’, Algebra Number Theory 9(9) (2015), 2167–2196.Google Scholar
Matomäki, K., Radziwiłł, M. and Tao, T., ‘Sign patterns of the Liouville and Möbius functions’, Forum Math. Sigma 4(e14) (2016), 44.Google Scholar
Matomäki, K., Radziwiłł, M. and Tao, T., ‘Fourier uniformity of bounded multiplicative functions in short intervals on average’, Preprint, 2018.Google Scholar
McNamara, R., ‘Sarnak’s conjecture for sequences of almost quadratic word growth’, Preprint, 2019.Google Scholar
Pollard, J. M., ‘A generalisation of the theorem of Cauchy and Davenport’, J. Lond. Math. Soc. (2) 8 (1974), 460–462.Google Scholar
Sós, V. T., ‘Turbulent years: Erdős in his correspondence with Turán from 1934 to 1940’, inPaul Erdős and His Mathematics, I (Budapest, 1999), Bolyai Soc. Math. Stud., 11 (János Bolyai Math. Soc., Budapest, 2002), 85–146.Google Scholar
Tao, T., ‘A variant of Kemperman’s theorem’, https://terrytao.wordpress.com/2011/12/26/.Google Scholar
Tao, T., ‘The logarithmically averaged Chowla and Elliott conjectures for two-point correlations’, Forum Math. Pi 4(e8) (2016), 36.Google Scholar
Tao, T., ‘Equivalence of the logarithmically averaged Chowla and Sarnak conjectures’, inNumber Theory—Diophantine Problems, Uniform Distribution and Applications (Springer, Cham, 2017).Google Scholar
Tao, T., ‘An inverse theorem for an inequality of Kneser’, Proc. Steklov Inst. Math. 303(1) (2018), 193–219. Published in Russian in Tr. Mat. Inst. Steklova 303 (2018) 209–238.Google Scholar
Tao, T. and Teräväinen, J., ‘Odd order cases of the logarithmically averaged chowla conjecture’, J. Théor. Nombres Bordeaux 30(3) (2018), 997–1015.Google Scholar
Tao, T. and Teräväinen, J., ‘The structure of logarithmically averaged correlations of multiplicative functions, with applications to the Chowla and Elliott conjectures’, Duke Math. J. 168(11) (2019), 1977–2027.Google Scholar
Teräväinen, J., ‘On binary correlations of multiplicative functions’, Forum Math. Sigma 6(e10) (2018), 41.Google Scholar
Wang, Z., ‘Sur les plus grands facteurs premiers d’entiers consécutifs’, Mathematika 64(2) (2018), 343–379.Google Scholar
Wooley, T. D. and Ziegler, T. D., ‘Multiple recurrence and convergence along the primes’, Amer. J. Math. 134(6) (2012), 1705–1732.Google Scholar
Ziegler, T., ‘Universal characteristic factors and Furstenberg averages’, J. Amer. Math. Soc. 20(1) (2007), 53–97.Google Scholar