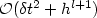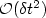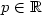We illustrate how some interesting new variational principles can beused for the numerical approximation of solutions to certain (possiblydegenerate) parabolic partial differential equations. One remarkablefeature of the algorithms presented here is that derivatives do notenter into the variational principles, so, for example, discontinuousapproximations may be used for approximating the heat equation. Wepresent formulae for computing a Wasserstein metric which entersinto the variational formulations.

In this short note we correct a conceptual error in theheuristic derivation of a kinetic equation used for thedescription of a one-dimensional granular medium in the socalled quasi-elastic limit, presented by the same authors inreference[1]. The equation we derived is however correct so that,the rigorous analysis on this equation, which constituted themain purpose of that paper, remains unchanged.

We study the asymptotic behaviour of the following nonlinear problem: $$\{\begin{array}{ll}-{\rm div}(a( Du_h))+\vert u_h\vert^{p-2}u_h =f \quad\hbox{in }\Omega_h, a( Du_h)\cdot\nu = 0 \quad\hbox{on }\partial\Omega_h, \end{array}.$$

in a domain Ωh of $\mathbb{R}^n$ whose boundary ∂Ωh contains an oscillating part with respect to hwhen h tends to ∞. The oscillating boundary is defined by a set of cylinders with axis 0xn that are h -1-periodically distributed. We prove that the limit problem in the domain corresponding tothe oscillating boundary identifieswith a diffusion operator with respect tox n coupled with an algebraic problemfor the limit fluxes.

The Navier–Stokes equations are approximated by means ofa fractional step, Chorin–Temam projection method; the time derivativeis approximated by a three-level backward finite difference, whereasthe approximation in space is performed by a Galerkin technique.It is shown that the proposed scheme yields an errorof ${\cal O}(\delta t^2 + h^{l+1})$ for the velocity in the norm of l 2(L2(Ω)d), where l ≥ 1 isthe polynomial degree of the velocity approximation. It is also shownthat the splitting error of projection schemes based on theincremental pressure correction is of ${\cal O}(\delta t^2)$ independent of theapproximation order of the velocity time derivative.

In the case of an elastic strip we exhibit two properties ofdispersion curves λn,n ≥ 1, that were not pointed outpreviously. We show cases where λ'n(0) = λ''n(0) = λ'''n(0) = 0 and we point out that these curves are not automatically monotoneous on ${\mathbb{R}}_{+}$ 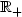. The non monotonicity was an open question (see [2],for example) and, for the first time, we give a rigourous answer. Recall thecharacteristic property of the dispersion curves: {λn(p);n ≥ 1} isthe set of eigenvalues of A p , counted with their multiplicity. Theoperators Ap , $p\in{\mathbb{R}}$ 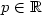, are the reduced operators deduced from the elasticoperator A using a partial Fourier transform. The second goal of this article is the introduction of a dispersion relationD(p,λ) = 0 in a general framework, and not only for a homogeneous situation(in this last case the relation is explicit). Recall that a dispersionrelation isan implicit equation the solutions of which are eigenvalues of A p . The mainproperty of the function D that we build is the following one: themultiplicity of an eigenvalue λ of A p is equal to the multiplicity ithas as a root of D(p,λ) = 0. We give also some applications.

This note deals with the approximation, by a P 1 finite element method with numerical integration,of solution curves of a semilinear problem. Because of both mixed boundary conditions and geometrical properties of the domain, some of the solutions do not belong to H 2. So, classical results for convergence lead to poor estimates. We show how to improve such estimates with the use of weighted Sobolev spaces together with a mesh“a priori adapted” to the singularity. For the H 1 or L 2-norms,we achieve optimal results.

We consider coupled structures consisting of two different linear elastic materials bonded along an interface. The material discontinuities combined with geometrical peculiarities of the outer boundary lead to unbounded stresses. The mathematical analysis of the singular behaviour of the elastic fields, especially near points where the interface meets the outer boundary, can be performed by means of asymptotic expansions with respect to the distance from the geometrical and structural singularities. The coefficients in the asymptotics, which are called generalized stress intensity factors, play an important role in classical fracture criteria. In this paper we present several formulas for the generalized stress intensity factors for 2D and 3D coupled elastic structures. The formulas have the form of scalar products or convolution integrals of the given data or the unknown displacement field and the so–called weight functions, similar to Maz'ya/Plamenevsky functionals introduced in [19] for elliptic boundary value problems. The weight functions are non–energetic elastic fields, which admit a decomposition into a known singular part and a more regular one, which is computed by boundary element domain decomposition methods. Numerical experiments for two–dimensional problems illustrate the theoretical results.

We show that Boltzmann's collision operator can be written explicitlyin divergence and double divergence forms. These conservativeformulations may be of interest for both theoretical and numericalpurposes. We give an application to the asymptotics of grazing collisions.