We consider the question raised in [1] of whether relaxed energy densities involving both bulk and surface energies can be written as a sum of two functions, one depending on the net gradient of admissible functions, and the other on net singular part. We show that, in general, they cannot. In particular, if the bulk density is quasiconvex but not convex, there exists a convex and homogeneous of degree 1 function of the jump such that there is no such representation.

Integral representation of relaxed energies and of Γ-limits of functionals $$ (u,v)\mapsto \int_\Omega f( x,u(x),v(x))\,dx $$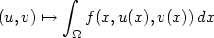 are obtained when sequences of fields v may develop oscillations and are constrained to satisfy a system of first order linear partial differential equations. This framework includes the treatement of divergence-free fields, Maxwell's equations in micromagnetics, and curl-free fields. In the latter case classical relaxation theorems in W1,p, are recovered.

We give necessary and sufficient conditions which characterize the Young measures associated to two oscillating sequences of functions, un on $\omega_1\times \omega_2$ and vn on $\omega_2$ satisfying the constraint $v_n(y)=\frac{1}{|\omega_1|} \int_{\omega_1} u_n (x, y) dx$. Our study is motivated by nonlinear effects induced by homogenization. Techniques based on equimeasurability and rearrangements are employed.

The problem of boundary stabilization for the isotropic linear elastodynamic system and the wave equation with Ventcel's conditions are considered (see [12]). The boundary observability and the exact controllability were etablished in [11]. We prove here the enegy decay to zero for the elastodynamic system with stationary Ventcel's conditions by introducing a nonlinear boundary feedback. We also give a boundary feedback leading to arbitrarily large energy decay rates for the elastodynamic system with evolutive Ventcel's conditions. A spectral study proves, finally, that the natural feedback is not sufficient to assure the exponential decay in the case of the wave equation with Ventcel's conditions.