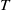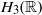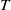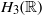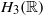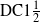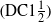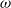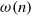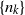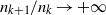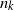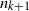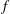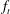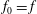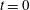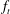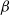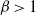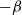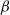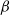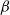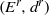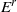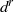Research Article
A Juzvinskii addition theorem for finitely generated free group actions
-
- Published online by Cambridge University Press:
- 01 November 2012, pp. 95-109
-
- Article
- Export citation
Multifractal formalism for Benedicks–Carleson quadratic maps
-
- Published online by Cambridge University Press:
- 11 March 2013, pp. 1116-1141
-
- Article
- Export citation
Geometric realization for substitution tilings
-
- Published online by Cambridge University Press:
- 05 December 2012, pp. 457-482
-
- Article
- Export citation
Some properties of positive entropy maps
-
- Published online by Cambridge University Press:
- 15 January 2013, pp. 765-776
-
- Article
- Export citation
Mixing actions of the Heisenberg group
-
- Published online by Cambridge University Press:
- 21 January 2013, pp. 1142-1167
-
- Article
- Export citation
Measure-theoretic chaos
-
- Published online by Cambridge University Press:
- 31 August 2012, pp. 110-131
-
- Article
- Export citation
Natural boundary for the susceptibility function of generic piecewise expanding unimodal maps
-
- Published online by Cambridge University Press:
- 25 January 2013, pp. 777-800
-
- Article
- Export citation
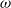 $\omega $-recurrence in skew products
$\omega $-recurrence in skew products
-
- Published online by Cambridge University Press:
- 03 April 2013, pp. 1525-1537
-
- Article
- Export citation
Intrinsic ergodicity via obstruction entropies
-
- Published online by Cambridge University Press:
- 03 April 2013, pp. 1816-1831
-
- Article
- Export citation
The entropy of a special overlapping dynamical system
-
- Published online by Cambridge University Press:
- 30 November 2012, pp. 483-500
-
- Article
- Export citation
Non-recurrence sets for weakly mixing linear dynamical systems
-
- Published online by Cambridge University Press:
- 24 August 2012, pp. 132-152
-
- Article
- Export citation
Lyapunov exponents in Hilbert geometry
-
- Published online by Cambridge University Press:
- 03 December 2012, pp. 501-533
-
- Article
- Export citation
Sharp polynomial bounds on the number of Pollicott–Ruelle resonances
-
- Published online by Cambridge University Press:
- 11 March 2013, pp. 1168-1183
-
- Article
- Export citation
Regular or stochastic dynamics in families of higher-degree unimodal maps
-
- Published online by Cambridge University Press:
- 03 April 2013, pp. 1538-1566
-
- Article
- Export citation
Distribution of approximants and geodesic flows
-
- Published online by Cambridge University Press:
- 03 June 2013, pp. 1832-1848
-
- Article
- Export citation
Law of large numbers for certain cylinder flows
-
- Published online by Cambridge University Press:
- 23 January 2013, pp. 801-825
-
- Article
- Export citation
Quantitative ergodic theorems for weakly integrable functions
-
- Published online by Cambridge University Press:
- 29 November 2012, pp. 534-542
-
- Article
- Export citation
Summability implies Collet–Eckmann almost surely
-
- Published online by Cambridge University Press:
- 21 January 2013, pp. 1184-1209
-
- Article
- Export citation
Isomorphisms between positive and negative
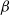 $\beta $-transformations
$\beta $-transformations
-
- Published online by Cambridge University Press:
- 09 November 2012, pp. 153-170
-
- Article
- Export citation
Continuation and bifurcation associated to the dynamical spectral sequence
-
- Published online by Cambridge University Press:
- 05 July 2013, pp. 1849-1887
-
- Article
- Export citation