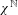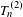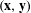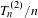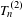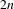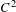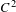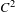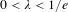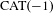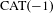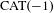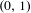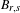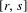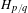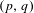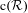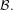Original Article
From the divergence between two measures to the shortest path between two observables
-
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1729-1744
-
- Article
- Export citation
Is a typical bi-Perron algebraic unit a pseudo-Anosov dilatation?
-
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1745-1750
-
- Article
- Export citation
On the dimension of triangular self-affine sets
-
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1751-1783
-
- Article
- Export citation
On the finiteness of attractors for piecewise
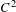 $C^{2}$ maps of the interval
$C^{2}$ maps of the interval
-
- Published online by Cambridge University Press:
- 04 December 2017, pp. 1784-1804
-
- Article
- Export citation
Hyperbolicity versus non-hyperbolic ergodic measures inside homoclinic classes
-
- Published online by Cambridge University Press:
- 07 November 2017, pp. 1805-1823
-
- Article
- Export citation
On the differentiability of hairs for Zorich maps
-
- Published online by Cambridge University Press:
- 07 November 2017, pp. 1824-1842
-
- Article
- Export citation
Surface groups acting on
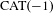 $\text{CAT}(-1)$ spaces
$\text{CAT}(-1)$ spaces
-
- Published online by Cambridge University Press:
- 04 December 2017, pp. 1843-1856
-
- Article
- Export citation
Optimal state amalgamation is NP-hard
-
- Published online by Cambridge University Press:
- 07 November 2017, pp. 1857-1869
-
- Article
- Export citation
Non-monotone periodic orbits of a rotational horseshoe
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 1870-1903
-
- Article
- Export citation
Strongly ergodic equivalence relations: spectral gap and type III invariants
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 1904-1935
-
- Article
- Export citation
Lower bounds for the decay of correlations in non-uniformly expanding maps
-
- Published online by Cambridge University Press:
- 07 November 2017, pp. 1936-1970
-
- Article
- Export citation
Birkhoff sum fluctuations in substitution dynamical systems
-
- Published online by Cambridge University Press:
- 07 September 2017, pp. 1971-2005
-
- Article
- Export citation
Cocycle rigidity of partially hyperbolic abelian actions with almost rank-one factors
-
- Published online by Cambridge University Press:
- 27 November 2017, pp. 2006-2016
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 39 Issue 7 Cover and Front matter
-
- Published online by Cambridge University Press:
- 04 June 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 39 Issue 7 Cover and Back matter
-
- Published online by Cambridge University Press:
- 04 June 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation