Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T21:28:57.846Z Has data issue: false hasContentIssue false
  • English
  • Français

Surface groups acting on 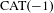$\text{CAT}(-1)$ spaces

Published online by Cambridge University Press:  04 December 2017

GEORGIOS DASKALOPOULOS ,
CHIKAKO MESE ,
ANDREW SANDERS  and
ALINA VDOVINA
GEORGIOS DASKALOPOULOS
Affiliation:
Mathematics Department, Box 1917, Brown University, Providence, RI 02912, USA email [email protected]
CHIKAKO MESE
Affiliation:
Department of Mathematics, Johns Hopkins University, 3400 N. Charles Street, Baltimore, MD 21218, USA email [email protected]
ANDREW SANDERS
Affiliation:
Mathematisches Institut, Universitat Heidelberg, Mathematikon, Im Neuenheimer Feld 205, 69120 Heidelberg, Germany email [email protected]
ALINA VDOVINA
Affiliation:
School of Mathematics and Statistics, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Harmonic map theory is used to show that a convex cocompact surface group action on a 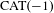$\text{CAT}(-1)$ metric space fixes a convex copy of the hyperbolic plane (i.e. the action is Fuchsian) if and only if the Hausdorff dimension of the limit set of the action is equal to 1. This provides another proof of a result of Bonk and Kleiner. More generally, we show that the limit set of every convex cocompact surface group action on a 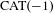$\text{CAT}(-1)$ space has Hausdorff dimension 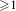$\geq 1$, where the inequality is strict unless the action is Fuchsian.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 7 , July 2019 , pp. 1843 - 1856
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bonk, M. and Kleiner, B.. Rigidity for quasi-Fuchsian actions on negatively curved spaces. Int. Math. Res. Not. IMRN 2004(61) (2004), 3309–3316.Google Scholar
Bourdon, M.. Structure conforme au bord et flot géodésique d’un CAT(-1) espace. Enseign. Math. 41 (1995), 63–102.Google Scholar
Bowen, R.. Hausdorff dimension of quasicircles. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 11–25.Google Scholar
Coornaert, M.. Mesures de Patterson–Sullivan sur le bord d’un espace hyperbolique au sens de Gromov. Pacific J. Math. 159 (1993), 241–270.Google Scholar
Deroin, B. and Tholozan, N.. Dominating surface group representations by Fuchsian ones. Int. Math. Res. Not. IMRN 2016 (2016), 4145–4166.Google Scholar
Goldman, W. and Wentworth, R.. Energy of twisted harmonic maps of Riemann surfaces. In the Tradition of Ahlfors–Bers. IV (Contemporary Mathematics, 432) . American Mathematical Society, Providence, RI, 2007, pp. 45–61.Google Scholar
Korevaar, N. and Schoen, R.. Sobolev spaces and harmonic maps into metric space targets. Comm. Anal. Geom. 1 (1993), 561–659.Google Scholar
Korevaar, N. and Schoen, R.. Global existence theorem for harmonic maps to non-locally compact spaces. Comm. Anal. Geom. 5 (1997), 333–387.Google Scholar
Manning, A.. Topological entropy for geodesic flows. Ann. of Math. (2) 110 (1979), 567–573.Google Scholar
Manning, A.. Curvature bounds for the entropy of the geodesic flow on a surface. J. Lond. Math. Soc. 24 (1981), 351–357.Google Scholar
Mese, C.. The curvature of minimal surfaces in singular spaces. Comm. Anal. Geom. 9 (2001), 3–34.Google Scholar
Sanders, A.. Entropy, minimal surfaces and negatively curved manifolds. Ergod. Th. & Dynam. Sys. Published online 4 July 2016, doi:10.1017/etds.2016.23.Google Scholar
Schoen, R. and Yau, S. T.. Existence of incompressible minimal surfaces and the topology of three dimensional manifolds with non-negative scalar curvature. Ann. of Math. (2) 110 (1979), 127–142.Google Scholar