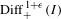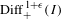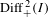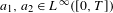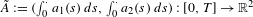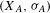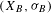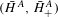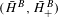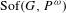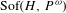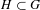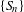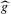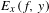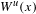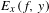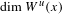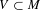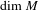Research Article
Extension of Hölder’s theorem in
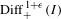 $\text{Diff}_{+}^{\,1+{\it\epsilon}}(I)$
$\text{Diff}_{+}^{\,1+{\it\epsilon}}(I)$
-
- Published online by Cambridge University Press:
- 11 February 2015, pp. 1343-1353
-
- Article
- Export citation
Polynomial multiple recurrence over rings of integers
-
- Published online by Cambridge University Press:
- 06 February 2015, pp. 1354-1378
-
- Article
- Export citation
Universal curves in the center problem for Abel differential equations
-
- Published online by Cambridge University Press:
- 15 December 2014, pp. 1379-1395
-
- Article
- Export citation
A note on operator semigroups associated to chaotic flows
-
- Published online by Cambridge University Press:
- 11 February 2015, pp. 1396-1408
-
- Article
- Export citation
Corrigendum
A note on operator semigroups associated to chaotic flows – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 01 December 2015, pp. 1409-1410
-
- Article
-
- You have access
- Export citation
Research Article
Functorial properties of Putnam’s homology theory for Smale spaces
-
- Published online by Cambridge University Press:
- 19 March 2015, pp. 1411-1440
-
- Article
- Export citation
Lyapunov spectrum for multimodal maps
-
- Published online by Cambridge University Press:
- 19 March 2015, pp. 1441-1493
-
- Article
- Export citation
On the ergodicity of hyperbolic Sinaĭ–Ruelle–Bowen measures: the constant unstable dimension case
-
- Published online by Cambridge University Press:
- 11 February 2015, pp. 1494-1515
-
- Article
- Export citation
Random affine code tree fractals and Falconer–Sloan condition
-
- Published online by Cambridge University Press:
- 15 December 2014, pp. 1516-1533
-
- Article
- Export citation
Computability of the packing measure of totally disconnected self-similar sets
-
- Published online by Cambridge University Press:
- 06 February 2015, pp. 1534-1556
-
- Article
- Export citation
Continuous orbit equivalence of topological Markov shifts and dynamical zeta functions
-
- Published online by Cambridge University Press:
- 06 February 2015, pp. 1557-1581
-
- Article
- Export citation
Shadowing, thick sets and the Ramsey property
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. 1582-1595
-
- Article
- Export citation
Convex structures revisited
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. 1596-1615
-
- Article
- Export citation
Compound Poisson statistics for multiple returns in shrinking cylinders for mixing processes
-
- Published online by Cambridge University Press:
- 11 February 2015, pp. 1616-1643
-
- Article
- Export citation
On non-contractible periodic orbits for surface homeomorphisms
-
- Published online by Cambridge University Press:
- 19 March 2015, pp. 1644-1655
-
- Article
- Export citation
Schmidt games and non-dense forward orbits of certain partially hyperbolic systems
-
- Published online by Cambridge University Press:
- 11 February 2015, pp. 1656-1678
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 36 Issue 5 Cover and Front matter
-
- Published online by Cambridge University Press:
- 29 June 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 36 Issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 29 June 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation