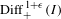Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T04:25:52.312Z Has data issue: false hasContentIssue false
  • English
  • Français

Extension of Hölder’s theorem in $\text{Diff}_{+}^{\,1+{\it\epsilon}}(I)$

Published online by Cambridge University Press:  11 February 2015

AZER AKHMEDOV
AZER AKHMEDOV*
Affiliation:
Department of Mathematics, North Dakota State University, Fargo, ND 58108, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that if ${\rm\Gamma}$ is a subgroup of 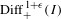$\text{Diff}_{+}^{\,1+{\it\epsilon}}(I)$ and 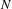$N$ is a natural number such that every non-identity element of ${\rm\Gamma}$ has at most $N$ fixed points, then ${\rm\Gamma}$ is solvable. If in addition ${\rm\Gamma}$ is a subgroup of 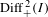$\text{Diff}_{+}^{\,2}(I)$, then we can claim that ${\rm\Gamma}$ is meta-abelian.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 5 , August 2016 , pp. 1343 - 1353
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhmedov, A.. A weak Zassenhaus lemma for subgroups of Diff(I). Algebr. Geom. Topol. 14(1) (2014), 539–550.Google Scholar
Barbot, T.. Characterization des flots d’Anosov en dimension 3 par leurs feuilletages faibles. Ergod. Th. & Dynam. Sys. 15(2) (1995), 247–270.Google Scholar
Farb, B. and Franks, J.. Groups of homeomorphisms of one-manifolds II: extension of Hölder’s theorem. Trans. Amer. Math. Soc. 355(11) (2003), 4385–4396.Google Scholar
Kovacevic, N.. Möbius-like groups of homeomorphisms of the circle. Trans. Amer. Math. Soc. 351(12) (1999), 4791–4822.Google Scholar
Navas, A.. Groups of Circle Diffeomorphisms (Chicago Lectures in Mathematics) . University of Chicago Press, Chicago, 2011.Google Scholar