Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T04:30:11.740Z Has data issue: false hasContentIssue false
  • English
  • Français

On non-contractible periodic orbits for surface homeomorphisms

Published online by Cambridge University Press:  19 March 2015

FÁBIO ARMANDO TAL
FÁBIO ARMANDO TAL*
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, Rua do Matão 1010, Cidade Universitária, 05508-090 São Paulo, SP, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work we study homeomorphisms of closed orientable surfaces homotopic to the identity, focusing on the existence of non-contractible periodic orbits. We show that, if $g$ is such a homeomorphism, and if ${\hat{g}}$ is its lift to the universal covering of $S$ that commutes with the deck transformations, then one of the following three conditions must be satisfied: (1) the set of fixed points for 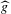${\hat{g}}$ projects to a closed subset $F$ which contains an essential continuum; (2) $g$ has non-contractible periodic points of every sufficiently large period; or (3) there exists a uniform bound 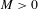$M>0$ such that, if $\hat{x}$ projects to a contractible periodic point, then the 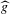${\hat{g}}$ orbit of 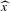$\hat{x}$ has diameter less than or equal to 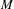$M$. Some consequences for homeomorphisms of surfaces whose rotation set is a singleton are derived.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 5 , August 2016 , pp. 1644 - 1655
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Addas-Zanata, S.. Area-preserving diffeomorphisms of the torus whose rotation sets have non-empty interior. Ergod. Th. & Dynam. Sys. (2014), to appear. Published online doi:10.1017/etds.2013.44.Google Scholar
Boyland, P., Guaschi, J. and Hall, T.. L’ensemble de rotation des homeomorphismes pseudo-Anosov. C. R. Acad. Sci., Paris 316 (1993), 1077–1080.Google Scholar
Brown, M. and Kister, J. M.. Invariance of complementary domains of a fixed point set. Proc. Amer. Math. Soc. 91 (1984), 503–504.Google Scholar
Biran, P., Polterovich, L. and Salamon, D.. Propagation in Hamiltonian dynamics and relative symplectic homology. Duke Math. J. 119 (2003), 65–118.Google Scholar
Fathi, A., Laudenbach, F. and Poenaru, V.. Travaux de Thurston sur les surfaces. Astérisque 66–67 (1979).Google Scholar
Franks, J.. Geodesics on S 2 and periodic points of annulus homeomorphisms. Invent. Math. 108 (1992), 403–418.CrossRefGoogle Scholar
Franks, J. and Handel, M.. Periodic points of Hamiltonian surface diffeomorphisms. Geom. Topol. 7 (2003), 713–756.CrossRefGoogle Scholar
Gatien, D. and Lalonde, F.. Holomorphic cylinders with Lagrangian boundaries and Hamiltonian dynamics. Duke Math. J. 102 (2000), 485–511.Google Scholar
Ginzburg, V. L.. The Conley conjecture. Ann. of Math. (2) 172 (2010), 1127–1180.CrossRefGoogle Scholar
Gürel, B. Z.. On non-contractible periodic orbits of Hamiltonian diffeomorphisms. Bull. Lond. Math. Soc. 45(6) (2013), 1227–1334.Google Scholar
Handel, M.. Global shadowing of pseudo-Anosov homeomorphisms. Ergod. Th. & Dynam. Sys. 5 (1985), 373–377.Google Scholar
Handel, M.. The rotation set of a homeomorphism of the annulus is closed. Comm. Math. Phys. 127 (1990), 339–349.Google Scholar
Hingston, N.. Subharmonic solutions of Hamiltonian equations on tori. Ann. of Math. (2) 170(2) 529–560.Google Scholar
Jäger, T.. Elliptic stars in a chaotic night. J. Lond. Math. Soc. (2) 84(3) (2011), 595–611.Google Scholar
Jaulent, O.. Existence d’un feuilletage positivement transverse à un homéomorphisme de surface. Ann. Inst. Fourier (Grenoble) 64 (2014), to appear.Google Scholar
Koropecki, A. and Tal, F. A.. Strictly toral dynamics. Invent. Math. 196(2) (2013), 339–381.Google Scholar
Koropecki, A. and Tal, F. A.. Area-preserving irrotational diffeomorphisms of the torus with sublinear diffusion. Proc. Amer. Math. Soc. 142 (2014), 3483–3490.CrossRefGoogle Scholar
Koropecki, A. and Tal, F. A.. Bounded and unbounded behavior for area-preserving rational pseudo-rotations. Proc. Lond. Math. Soc. (3) 109(3) (2014), 785–822.CrossRefGoogle Scholar
Koropecki, A. and Tal, F. A.. Boundedness of invariant domains for surface homeomorphisms. Preprint, 2013.Google Scholar
Le Calvez, P.. Une version feuilletée équivariante du théorème de translation de Brouwer. Publ. Math. Inst. Hautes Études Sci.(102) (2005), 1–98.Google Scholar
Le Calvez, P.. Periodic orbits of Hamiltonian homeomorphisms of surfaces. Duke Math. J. 133 (2006), 125–184.Google Scholar
Salomão, P. and Weber, J.. An almost existence theorem for non-contractible periodic orbits in cotangent bundles. São Paulo J. Math. Sci. 6(2) (2012), 385–394.Google Scholar
Weber, J.. Noncontractible periodic orbits in cotangent bundles and Floer homology. Duke Math. J. 133 (2006), 527–568.Google Scholar