Research Article
Minimal flows of finite almost periodic rank
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 155-172
-
- Article
-
- You have access
- Export citation
Duality for automorphisms on a compact C*-dynamical system
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 173-189
-
- Article
-
- You have access
- Export citation
Some compact invariant sets for hyperbolic linear automorphisms of torii
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 191-204
-
- Article
-
- You have access
- Export citation
The attracting centre of a continuous self-map of the interval
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 205-213
-
- Article
-
- You have access
- Export citation
Geodesic flows of negatively curved manifolds with smooth stable and unstable foliations†
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 215-239
-
- Article
-
- You have access
- Export citation
Propriétés des attracteurs de Birkhoff
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 241-310
-
- Article
-
- You have access
- Export citation
On the construction of smooth ergodic skew-products†
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 311-326
-
- Article
-
- You have access
- Export citation
Book Review
Dynamical Systems and Singular PhenomenaIn World scientific advanced series in dynamical systems, G. Ikegami (ed.) Vol. 2, World Scientific Publishers, Singapore, 1987, x + 244 pp, ISBN 9971-50-231-3
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 327-328
-
- Article
-
- You have access
- Export citation
Front matter
ETS volume 8 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
ETS volume 8 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation


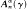 to be the subspace
to be the subspace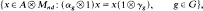
 .
. −Γ is either empty or countably infinite, where
−Γ is either empty or countably infinite, where 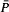 denotes the closure of the set
denotes the closure of the set 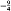 and −1 strictly.
and −1 strictly.