Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T04:14:23.582Z Has data issue: false hasContentIssue false
  • English
  • Français

The attracting centre of a continuous self-map of the interval

Published online by Cambridge University Press:  19 September 2008

Xiong Jincheng
Xiong Jincheng
Affiliation:
University of Science and Technology of China, Hefei, Anhui, People's Republic of China and International Centre for Theoretical Physics, Trieste, Italy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ƒ denote a continuous map of a compact interval I to itself. A point x ∈ I is called a γ-limit point of ƒ if it is both an ω-limit point and an α-limit point of some point y ∈ I. Let Γ denote the set of γ-limit points. In the present paper, we show that (1) −Γ is either empty or countably infinite, where 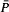denotes the closure of the set P of periodic points, (2) x ∈ I is a γ-limit point if and only if there exist y1 and y2 in I such that x is an ω-limit point of y1, and y1 is an ω-limit point of y2, and if and only if there exists a sequence y1, y2,…of points in I such that x is an ω-limit point of y1, and yi is an ω-limit point of yi+1 for every i ≥ 1, and (3) the period of each periodic point of ƒ is a power of 2 if and only if every γ-limit point is recurrent.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 8 , Issue 2 , June 1988 , pp. 205 - 213
Copyright
Copyright © Cambridge University Press 1988

References

REFERENCES

[1]Block, L. & Coven, E., ω-limit sets for maps of the interval. Preprint, Wesleyan Univ., 1985.Google Scholar
[2]Chu, H. & Xiong, J.-C.. A counterexample in dynamical systems of the interval. Proc. Amer. Math. Soc. 97 (1986), 361–366.CrossRefGoogle Scholar
[3]Coppel, W. A.. Maps of an interval. IMA Preprint Series #26, 1983.Google Scholar
[4]Coppel, W. A.. Continuous maps of the interval. Xeroxed notes, 1984.Google Scholar
[5]Coven, E. & Nitecki, Z.. Non-wandering sets of the powers of maps of the interval. Ergod. Th. Dynam. Sys., 1 (1981), 9–31.Google Scholar
[6]Sharkovskii, A. N.. On a theorem of G. D. Birkhoff. Dopovidi Akad. Nauk. Ukrain. RSR Ser. A, 1967, 429–432.Google Scholar
[7]Xiong, J.-C.. for every continuous self-map ƒ of the interval. Kexue Tongbao (Chinese Ed.) 27 (1982), 513–514, andGoogle Scholar
Kexue Tongbao (English Ed.) 28 (1983), 21–23.Google Scholar
[8]Xiong, J.-C.. Non-wandering sets of continuous interval self-maps. Kexue Tongbao (English Ed.) 29 (1984), 1432–1434.Google Scholar
[9]Xiong, J.-C.. Sets of recurrent points of continuous maps of the interval. Proc. Amer. Math. Soc. 95 (1985), 491–494.Google Scholar
[10]Xiong, J.-C.. Set of almost periodic points of a continuous self-map of an interval. Acta Mathematica Sinica (new series) 2 (1986), 73–77.Google Scholar