Research Article
Absolutely continuous conjugacy of expanding endomorphisms
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 225-230
-
- Article
- Export citation
Newton's method and a class of meromorphic functions without wandering domains
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 231-247
-
- Article
- Export citation
On the asymptotic range of cocyles for shifts of finite type
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 249-262
-
- Article
- Export citation
On the C2-creation of links of critical points
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 263-288
-
- Article
- Export citation
Amenable actions of discrete groups
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 289-318
-
- Article
- Export citation
Almost everywhere exponential convergence of the modified Jacobi—Perron algorithm
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 319-334
-
- Article
- Export citation
Lefschetz formulae for Anosov flows on 3-manifolds
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 335-347
-
- Article
- Export citation
Connectedness of the tricorn
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 349-356
-
- Article
- Export citation
Symplectic displacement energy for Lagrangian submanifolds
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 357-367
-
- Article
- Export citation
Homoclinic tangencies: moduli and topology of separatrices
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 369-385
-
- Article
- Export citation
Closed orbits in homology classes for Anosov flows
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 387-408
-
- Article
- Export citation
Some open sets of nonuniformly hyperbolic cocycles
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 409-415
-
- Article
- Export citation
Front matter
ETS volume 13 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
ETS volume 13 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

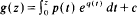 where
where 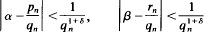
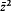 +
+