Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-04T19:33:01.920Z Has data issue: false hasContentIssue false
  • English
  • Français

Newton's method and a class of meromorphic functions without wandering domains

Published online by Cambridge University Press:  19 September 2008

Walter Bergweiler
Walter Bergweiler
Affiliation:
Lehrstuhl II für Mathematik, RWTH Aachen, Templergraben 55, D-5100 Aachen, Germany†
Get access Rights & Permissions [Opens in a new window]

Abstract

Let N be the class of meromorphic functions f with the following properties: f has finitely many poles;f′ has finitely many multiple zeros; the superattracting fixed points of f are zeros of f′ and vice versa, with finitely many exceptions; f has finite order. It is proved that if f ∈ N, then f does not have wandering domains. Moreover, if f ∈ N and if ∞ is among the limit functions of fn in a cycle of periodic domains, then this cycle contains a singularity of f−1. 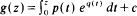(Here fn denotes the nth iterate of f) These results are applied to study Newton's method for entire functions g of the form where p and q are polynomials and where c is a constant. In this case, the Newton iteration function f(z) = z − g(z)/g′(z) is in N. It follows that fn(z) converges to zeros of g for all z in the Fatou set of f, if this is the case for all zeros z of g″. Some of the results can be extended to the relaxed Newton method.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 13 , Issue 2 , June 1993 , pp. 231 - 247
Copyright
Copyright © Cambridge University Press 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baker, I. N.. An entire function which has wandering domains. J. Australian Math. Soc. (Ser. A) 22 (1976), 173–176.CrossRefGoogle Scholar
[2]Baker, I. N.. Wandering domains in the iteration of entire functions. Proc. London Math. Soc. (3) 49 (1984), 563–576.CrossRefGoogle Scholar
[3]Baker, I. N.. Some entire functions with multiply-connected wandering domains. Ergod. Th. & Dynam. Sys. 5 (1985), 163–169.CrossRefGoogle Scholar
[4]Baker, I. N.. Iteration of entire functions: an introductory survey. In Lectures on Complex Analysis. World Scientific: Singapore, New Jersey, London, Hong Kong, 1987, pp. 1–17.Google Scholar
[5]Baker, I. N.. Infinite limits in the iteration of entire functions. Ergod. Th. & Dynam. Sys. 8 (1988), 503–507.CrossRefGoogle Scholar
[6]Baker, I. N., Kotus, J. & Yinian, L.. Iterates of meromorphic functions I. Ergod. Th. & Dynam. Sys. 11 (1991), 241–248.CrossRefGoogle Scholar
[7]Baker, I. N., Kotus, J. & Yinian, L.. Iterates of meromorphic functions II: Examples of wandering domains. J. London Math. Soc. (2) 42 (1990), 267–278.CrossRefGoogle Scholar
[8]Baker, I. N., Kotus, J. & Yinian, L.. Iterates of meromorphic functions III: Preperiodic domains. Ergod. Th. & Dynam. Sys. 11 (1991), 603–618.CrossRefGoogle Scholar
[9]Baker, I. N., Kotus, J. and Yinian, L.. Iterates of meromorphic functions IV: Critically finite functions. Results Math. 22 (1992), 651–656.CrossRefGoogle Scholar
[10]Beardon, A. F.. Iteration of Rational Functions. Springer: New York, Berlin, Heidelberg 1991.CrossRefGoogle Scholar
[11]Bergweiler, W., Haeseler, F. v., Kriete, H., Meier, H.-G. & Terglane, N.. Newton's method for meromorphic functions. Preprint.Google Scholar
[12]Blanchard, P.. Complex analytic dynamics on the Riemann sphere. Bull. Amer. Math. Soc. 11 (1984), 85–141.CrossRefGoogle Scholar
[13]Cremer, H.. Über die Schrödersche Funktionalgleichung und das Schwarzsche Eckenabbildungs problem. Ber. Verh. Sächs. Akad. Wiss. Leipzig, Math.-Phys. Kl. 84 (1932), 291–324.Google Scholar
[14]Devaney, R. L. & Keen, L.. Dynamics of meromorphic maps with polynomial Schwarzian derivative. Ann. Sci. École Norm. Sup. (4) 22 (1989), 55–81.CrossRefGoogle Scholar
[15]Eremenko, A. E. & Lyubich, M. Yu.. Iterates of entire functions. Sov. Math. Dokl. 30 (1984), 592–594; translation from Dokl. Akad. Nauk. SSSR 279 (1984).Google Scholar
[16]Eremenko, A. E. & Lyubich, M. Yu.. Examples of entire functions with pathological dynamics. J. London Math. Soc. (2) 36 (1987), 458–468.CrossRefGoogle Scholar
[17]Eremenko, A. E. & Lyubich, M. Yu.. The dynamics of analytic transforms. Leningrad Math. J. 1 (1990), 563–634.Google Scholar
[18]Eremenko, A. E. & Lyubich, M. Yu.. Dynamical properties of some classes of entire functions. Ann. Inst. Fourier 42 (1992), 989–1020.CrossRefGoogle Scholar
[19]Fatou, P.. Sur les équations fonctionelles. Bull. Soc. Math. France 47 (1919), 161–271; 48 (1920), 33–94, 208–314.Google Scholar
[20]Fatou, P.. Sur l'itération des fonctions transcendantes entières. Acta Math. 47 (1926), 337–360.CrossRefGoogle Scholar
[21]Goldberg, L. R. & Keen, L.. A finiteness theorem for a dynamical class of entire functions. Ergod. Th. & Dynam. Sys. 6 (1986), 183–192.CrossRefGoogle Scholar
[22]Haeseler, F. v. & Peitgen, H.-O.. Newton's method and complex dynamical systems, Acta Appl. Math. 13 (1988), 3–58;CrossRefGoogle Scholar
Newton's Method and Dynamical Systems. Peitgen, H.-O., ed. Kluwer Academic Publishers: Dordrecht 1989, pp 3–58.CrossRefGoogle Scholar
[23]Hayman, W. K.. Meromorphic Functions. Clarendon Press: Oxford, 1964.Google Scholar
[24]Herman, M.. Exemples de fractions rationelles ayant une orbite dense sur la sphère de Riemann. Bull. Soc. Math. France 112 (1984), 93–142.Google Scholar
[25]Herman, M.. Are there critical points on the boundary of singular domains. Commun. Math. Phys. 99 (1985), 593–612.CrossRefGoogle Scholar
[26]Hinkkanen, A.. Iteration and the zeros of the second derivative of a momorphic function. Proc. London Math. Soc. 65 (1992), 629–650.CrossRefGoogle Scholar
[27]Jank, G. & Volkmann, L.. Einführung in die Theorie der ganzen und meromorphen Funktionen mit Anwendungen auf Differentialgleichungen. Birkhäuser: Basel, Boston, Stuttgart, 1985.CrossRefGoogle Scholar
[28]Julia, G.. Sur l'itération des fonctions rationelles. J. Math. Pure Appl. (7) 4 (1918), 47–245.Google Scholar
[29]Lehto, O. & Virtanen, K. I.. Quasikonforme Abbildungen. Springer: Berlin, Heidelberg, New York, 1965.CrossRefGoogle Scholar
[30]Lyubich, M. Yu.. The dynamics of rational transforms: the topological picture. Russian Math. Surveys 41: 4 (1986), 43–117; translation from Uspekhi Mat. Nauk 41:4 (1986), 35–95.CrossRefGoogle Scholar
[31]Milnor, J.. Dynamics in one complex variable: introductory lectures. Stony Brook Institute for Mathematical Sciences. Preprint 1990/1995.Google Scholar
[32]Nevanlinna, R.. Analytic Functions. Springer: Berlin, Heidelberg, New York, 1970.CrossRefGoogle Scholar
[33]Stallard, G. W.. A class of meromorphic functions with no wandering domains. Ann. Acad. Sci. Fenn. 16 (1991), 211–226.CrossRefGoogle Scholar
[34]Steinmetz, N.. On Sullivan's classification of periodic stable domains. Complex Variables Theory Appl. 14 (1990), 211–214.Google Scholar
[35]Sullivan, D.. Itération des fonctions analytiques complexes. C.R. Acad. Sci. Paris 294 (1982), 301–303.Google Scholar
[36]Sullivan, D.. Quasiconformal homeomorphisms and dynamics I: Solution of the Fatou-Julia problem on wandering domains. Ann. Math. 122 (1985), 401–418.CrossRefGoogle Scholar
[37]Sullivan, D.. Quasiconformal homeomorphisms and dynamics III: Topological conjugacy classes of analytic endomorphisms. Preprint IHES/M/83/1, Institut des Hautes Etudes Scientifiques, 1983.Google Scholar
[38]Töpfer, H.. Komplexe Iterationsindizes ganzer und rationaler Funktionen. Math. Ann. 121 (1949), 191–222.CrossRefGoogle Scholar
[39]Tsuji, M.. Potential Theory in Modern Function Theory. Maruzen: Tokyo, 1959.Google Scholar