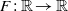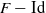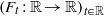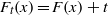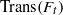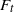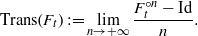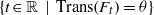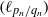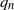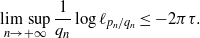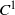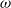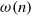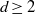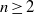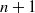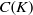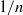Survey
The thermodynamic approach to multifractal analysis
-
- Published online by Cambridge University Press:
- 04 August 2014, pp. 1409-1450
-
- Article
- Export citation
Research Article
On the widths of the Arnol’d tongues
-
- Published online by Cambridge University Press:
- 03 May 2013, pp. 1451-1463
-
- Article
- Export citation
Rigidity and non-recurrence along sequences
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 1464-1502
-
- Article
- Export citation
A lower bound for topological entropy of generic non-Anosov symplectic diffeomorphisms
-
- Published online by Cambridge University Press:
- 03 April 2013, pp. 1503-1524
-
- Article
- Export citation
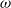 $\omega $-recurrence in skew products
$\omega $-recurrence in skew products
-
- Published online by Cambridge University Press:
- 03 April 2013, pp. 1525-1537
-
- Article
- Export citation
Regular or stochastic dynamics in families of higher-degree unimodal maps
-
- Published online by Cambridge University Press:
- 03 April 2013, pp. 1538-1566
-
- Article
- Export citation
Attractive regular stochastic chains: perfect simulation and phase transition
-
- Published online by Cambridge University Press:
- 03 April 2013, pp. 1567-1586
-
- Article
- Export citation
Topological structure and entropy of mixing graph maps
-
- Published online by Cambridge University Press:
- 30 April 2013, pp. 1587-1614
-
- Article
- Export citation
On local aspects of topological weak mixing, sequence entropy and chaos
-
- Published online by Cambridge University Press:
- 11 April 2013, pp. 1615-1639
-
- Article
- Export citation
Actions of discrete groups on stationary Lorentz manifolds
-
- Published online by Cambridge University Press:
- 05 June 2013, pp. 1640-1673
-
- Article
- Export citation
Topological Wiener–Wintner theorems for amenable operator semigroups
-
- Published online by Cambridge University Press:
- 04 April 2013, pp. 1674-1698
-
- Article
- Export citation
Aperiodic sequences and aperiodic geodesics
-
- Published online by Cambridge University Press:
- 14 March 2013, pp. 1699-1723
-
- Article
- Export citation
Polynomial decay of correlations in linked-twist maps
-
- Published online by Cambridge University Press:
- 04 April 2013, pp. 1724-1746
-
- Article
- Export citation
Cube spaces and the multiple term return times theorem
-
- Published online by Cambridge University Press:
- 14 March 2013, pp. 1747-1760
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 34 Issue 5 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 September 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 34 Issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 September 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation