Research Article
The mathematical research of William Parry FRS
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 321-337
-
- Article
- Export citation
Ledrappier’s system is almost mixing of all orders
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 339-365
-
- Article
- Export citation
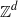 group shifts and Bernoulli factors
group shifts and Bernoulli factors
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 367-387
-
- Article
- Export citation
Particle drift in self-similar billiards
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 389-403
-
- Article
- Export citation
Ergodic fractal measures and dimension conservation
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 405-422
-
- Article
- Export citation
On spectral properties of a family of transfer operators and convergence to stable laws for affine random walks
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 423-446
-
- Article
- Export citation
Shannon entropy for stationary processes and dynamical systems
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 447-480
-
- Article
- Export citation
Flow–orbit equivalence for minimal Cantor systems
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 481-500
-
- Article
- Export citation
Thermodynamical formalism for robust classes of potentials and non-uniformly hyperbolic maps
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 501-533
-
- Article
- Export citation
An analogue of Bauer’s theorem for closed orbits of skew products
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 535-546
-
- Article
- Export citation
Addendum: An analogue of Artin reciprocity for closed orbits of skew products
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 547-552
-
- Article
- Export citation
Lifting measures to inducing schemes
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 553-574
-
- Article
- Export citation
Dynamics of two-dimensional Blaschke products
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 575-585
-
- Article
- Export citation
Large deviations in non-uniformly hyperbolic dynamical systems
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 587-612
-
- Article
- Export citation
Differentiation of SRB states for hyperbolic flows
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 613-631
-
- Article
- Export citation
Algebraic polymorphisms
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 633-642
-
- Article
- Export citation
Renewal-type limit theorem for the Gauss map and continued fractions
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 643-655
-
- Article
- Export citation
Norm convergence of multiple ergodic averages for commuting transformations
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 657-688
-
- Article
- Export citation
Two facts concerning the transformations which satisfy the weak Pinsker property
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 689-695
-
- Article
- Export citation
On the entropy of linear factors
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 697-705
-
- Article
- Export citation


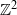 -action which is 2-mixing but not 3-mixing. Our main result is that, excluding certain small ‘constructible’ sets, the system is mixing of every order.
-action which is 2-mixing but not 3-mixing. Our main result is that, excluding certain small ‘constructible’ sets, the system is mixing of every order.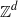 group shifts and Bernoulli factors
group shifts and Bernoulli factors
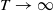 and {ln
and {ln 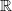 , and we study the Birkhoff sums associated with its trajectories. We show that, depending on the parameters of the random walk, the normalized Birkhoff sums converge in law to a stable law of exponent
, and we study the Birkhoff sums associated with its trajectories. We show that, depending on the parameters of the random walk, the normalized Birkhoff sums converge in law to a stable law of exponent 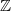 or
or 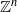 whose finite-dimensional marginals have laws which are absolutely continuous with respect to Lebesgue measure. We define an entropy theory for these continuous processes, prove an analogue of the Shannon–MacMillan–Breiman theorem and study more precisely the particular example of Gaussian processes.
whose finite-dimensional marginals have laws which are absolutely continuous with respect to Lebesgue measure. We define an entropy theory for these continuous processes, prove an analogue of the Shannon–MacMillan–Breiman theorem and study more precisely the particular example of Gaussian processes.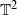 and
and 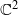 of a two-dimensional Blaschke product. We prove that in the case when the Blaschke product is a diffeomorphism of
of a two-dimensional Blaschke product. We prove that in the case when the Blaschke product is a diffeomorphism of 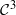 vector field
vector field 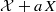 on
on 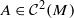 , then
, then 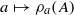 is
is 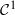 on (−ϵ,ϵ) and
on (−ϵ,ϵ) and 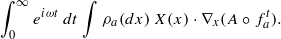
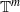 if and only if the associated rational matrix lies in
if and only if the associated rational matrix lies in 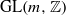 . We characterize toral polymorphisms which are factors of toral automorphisms.
. We characterize toral polymorphisms which are factors of toral automorphisms.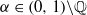 and
and 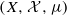 . We show that the multiple ergodic averages
. We show that the multiple ergodic averages 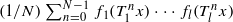 are convergent in
are convergent in 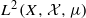 as
as 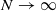 for all
for all 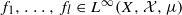 ; this was previously established for
; this was previously established for 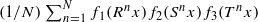 .
. 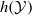 of a stationary process
of a stationary process 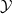 , which is a factor of the process
, which is a factor of the process 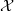 , can take any value in the interval
, can take any value in the interval 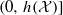 . For linear factors the situation is completely different. In fact it even matters how the class of linear factors is defined. We will investigate both moving averages of bounded sequences by coefficients in
. For linear factors the situation is completely different. In fact it even matters how the class of linear factors is defined. We will investigate both moving averages of bounded sequences by coefficients in