Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T03:53:14.070Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of two-dimensional Blaschke products

Published online by Cambridge University Press:  01 April 2008

ENRIQUE R. PUJALS  and
MICHAEL SHUB
ENRIQUE R. PUJALS
Affiliation:
IMPA Estrada Dona Castorina 110, Rio de Janeiro, Brasil 22460-320 (email: [email protected])
MICHAEL SHUB
Affiliation:
Math Department, University of Toronto, 40 St. George Street, Toronto, ON M5S 2E4, Canada (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the dynamics on 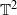and 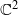of a two-dimensional Blaschke product. We prove that in the case when the Blaschke product is a diffeomorphism of 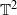with all periodic points hyperbolic then the dynamics is hyperbolic. If a two-dimensional Blaschke product diffeomorphism of 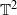is embedded in a two-dimensional family given by composition with translations of 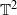, then we show that there is a non-empty open set of parameter values for which the dynamics is Anosov or has an expanding attractor with a unique SRB measure.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 2: William Parry Memorial Volume , April 2008 , pp. 575 - 585
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bonatti, C., Diaz, L. J. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective. Springer, 2005.Google Scholar
[2]Carleson, L. and Gamelin, T.. Complex Dynamics (Universitext: Tracts in Mathematics). Springer, 1993.CrossRefGoogle Scholar
[3]Franks, J.. Anosov diffeomorphisms. Global Analysis (Proceedings of Symposia in Pure Mathematics, XIV). American Mathematical Society, Providence, RI, 1970.Google Scholar
[4]Manning, A.. There are no new Anosov diffeomorphisms on tori. Amer. J. Math. 96 (1974), 422–429.CrossRefGoogle Scholar
[5]Pujals, E. R., Robert, L. and Shub, M.. Expanding maps of the circle rerevisited: positive Lyapunov exponents in a rich family. Ergod. Th. & Dynam. Sys. 26(6) (2006), 1931–1937.CrossRefGoogle Scholar
[6]Pujals, E. R. and Sambarino, M.. Homoclinic tangencies and hyperbolicity for surface diffeomorphisms. Ann. of Math. 151 (2000), 961–1023.CrossRefGoogle Scholar
[7]Pujals, E. R. and Sambarino, M.. On the dynamics of dominated splitting. Ann. of Math., to appear.Google Scholar
[8]Rudin, W.. Function Theory in Polydiscs. W.A. Benjamin, New York, 1969.Google Scholar
[9]Shub, M. and Sullivan, D.. A remark on the Lefschetz fixed point formula for differentiable maps. Topology 13 (1974), 189–191.CrossRefGoogle Scholar