Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T04:20:39.678Z Has data issue: false hasContentIssue false
  • English
  • Français

Norm convergence of multiple ergodic averages for commuting transformations

Published online by Cambridge University Press:  01 April 2008

TERENCE TAO
TERENCE TAO*
Affiliation:
UCLA Department of Mathematics, Los Angeles, CA 90095-1596, USA (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

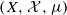Let T1,…,Tl:X→X be commuting measure-preserving transformations on a probability space . We show that the multiple ergodic averages 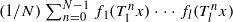are convergent in 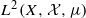as 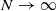for all 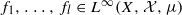; this was previously established for l=2 by Conze and Lesigne [J. P. Conze and E. Lesigne. Théorèmes ergodique por les mesures diagonales. Bull. Soc. Math. France112 (1984), 143–175] and for general l assuming some additional ergodicity hypotheses on the maps Ti and TiTj−1 by Frantzikinakis and Kra [N. Frantzikinakis and B. Kra. Convergence of multiple ergodic averages for some commuting transformations. Ergod. Th. & Dynam. Sys.25 (2005), 799–809] (with the l=3 case of this result established earlier by Zhang [Q. Zhang. On the convergence of the averages 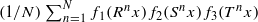. Mh. Math.122 (1996), 275–300]). Our approach is combinatorial and finitary in nature, inspired by recent developments regarding the hypergraph regularity and removal lemmas, although we will not need the full strength of those lemmas. In particular, the l=2 case of our arguments is a finitary analogue of those by Conze and Lesigne.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 2: William Parry Memorial Volume , April 2008 , pp. 657 - 688
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Avigad, J., Gerhardy, P. and Towsner, H.. Local stability of ergodic averages. Preprint.Google Scholar
[2]Berend, D. and Bergelson, V.. Jointly ergodic measure-preserving transformations. Israel J. Math. 49(4) (1984), 307–314.Google Scholar
[3]Conze, J. P. and Lesigne, E.. Théorèmes ergodique por les mesures diagonales. Bull. Soc. Math. France 112 (1984), 143–175.CrossRefGoogle Scholar
[4]Frantzikinakis, N. and Kra, B.. Convergence of multiple ergodic averages for some commuting transformations. Ergod. Th. & Dynam. Sys. 25 (2005), 799–809.CrossRefGoogle Scholar
[5]Frieze, A. and Kannan, R.. Quick approximation to matrices and applications. Combinatorica 19(2) (1999), 175–220.CrossRefGoogle Scholar
[6]Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.CrossRefGoogle Scholar
[7]Furstenberg, H.. Recurrence in Ergodic theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.Google Scholar
[8]Furstenberg, H. and Katznelson, Y.. An ergodic Szemerédi theorem for commuting transformations. J. Anal. Math. 34 (1978), 275–291.CrossRefGoogle Scholar
[9]Green, B. and Tao, T.. The primes contain arbitrarily long arithmetic progressions. Ann. Math. 167(2) (2008).Google Scholar
[10]Green, B. and Tao, T.. New bounds for Szemerédi’s theorem I: Progressions of length 4 in finite field geometries. Preprint.Google Scholar
[11]Gowers, T.. Hypergraph regularity and the multidimensional Szemerédi theorem. Preprint.Google Scholar
[12]Host, B. and Kra, B.. Non-conventional ergodic averages and nilmanifolds. Ann. Math. 161(1) (2005), 397–488.CrossRefGoogle Scholar
[13]Kohlenbach, U.. Effective bounds from proofs in abstract functional analysis. New Computational Paradigms: Changing Conceptions of What is Computable. Eds. B. Cooper, B. Löwe and A. Sorbi. Springer, Berlin, 2008, pp. 223–258.CrossRefGoogle Scholar
[14]Kreisel, G.. On the interpretation of non-finitist proofs, part I. J. Symbolic Logic 16 (1951), 241–267.Google Scholar
[15]Kriesel, G.. Interpretation of analysis by means of constructive functionals of finite type. Constructivity in Mathematics. Ed. A. Heyting. North-Holland, Amsterdam, 1959, pp. 101–128.Google Scholar
[16]Lesigne, E.. Équations fonctionelles, couplages de produits gauches et theéorèmes ergodique pour mesures diagonales. Bull. Soc. Math. France 121 (1993), 315–351.CrossRefGoogle Scholar
[17]Nagle, B., Rödl, V. and Schacht, M.. The counting lemma for regular k-uniform hypergraphs. Random Structures Algorithms 28(22) (2006), 113–179.CrossRefGoogle Scholar
[18]Paris, J. and Harrington, L.. A mathematical incompleteness in Peano arithmetic. Handbook for Mathematical Logic. Ed. J. Barwise. North-Holland, Amsterdam, Netherlands, 1977.Google Scholar
[19]Rödl, V. and Skokan, J.. Applications of the regularity lemma for uniform hypergraphs. Random Structures Algorithms 28(2) (2006), 180–194.Google Scholar
[20]Simic, K.. The pointwise ergodic theorem in subsystems of second-order arithmetic. Symbolic Logic 72 (2007), 45–66.CrossRefGoogle Scholar
[21]Solymosi, J.. Note on a generalization of Roth’s theorem. Discrete and Computational Geometry (Algorithms and Combinatorics, 25). Springer, Berlin, 2003, pp. 825–827.Google Scholar
[22]Szemerédi, E.. On sets of integers containing no k elements in arithmetic progression. Acta Arith. 27 (1975), 299–345.CrossRefGoogle Scholar
[23]Tao, T.. A variant of the hypergraph removal lemma. J. Combin. Theory Ser. A 113 (2006), 1257–1280.CrossRefGoogle Scholar
[24]Tao, T.. The Gaussian primes contain arbitrarily shaped constellations. J. Anal. Math. 99 (2006), 109–176.CrossRefGoogle Scholar
[25]Tao, T.. A correspondence principle between (hyper)graph theory and probability theory, and the (hyper)graph removal lemma. Preprint.Google Scholar
[26]Tao, T.. A quantitative version of the Besicovitch projection theorem via multiscale analysis. Preprint.Google Scholar
[27]Tao, T. and Ziegler, T.. The primes contain arbitrarily long polynomial progressions. Preprint.Google Scholar
[28]Wiener, N.. The ergodic theorem. Duke Math. J. 5 (1939), 1–18.CrossRefGoogle Scholar
[29]Yu, X.. Lebesgue convergence theorems and reverse mathematics. Math. Logic Quart. 40 (1994), 1–13.Google Scholar
[30]Zhang, Q.. On the convergence of the averages . Mh. Math. 122 (1996), 275–300.CrossRefGoogle Scholar
[31]Ziegler, T.. Universal characteristic factors and Furstenberg averages. J. Amer. Math. Soc. 20 (2007), 53–97.Google Scholar