Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T04:41:47.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower bounds for the decay of correlations in non-uniformly expanding maps

Published online by Cambridge University Press:  07 November 2017

HUYI HU  and
SANDRO VAIENTI
HUYI HU
Affiliation:
Mathematics Department, Michigan State University, East Lansing, MI 48824, USA email [email protected]
SANDRO VAIENTI
Affiliation:
Aix-Marseille Université, CNRS, CPT, UMR 7332, Marseille, France Université de Toulon, CNRS, CPT, UMR 7332, 83957 La Garde, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give conditions under which non-uniformly expanding maps exhibit lower bounds of polynomial type for the decay of correlations and for a large class of observables. We show that if the Lasota–Yorke-type inequality for the transfer operator of a first return map is satisfied in a Banach space 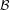${\mathcal{B}}$, and the absolutely continuous invariant measure obtained is weak mixing, in terms of aperiodicity, then, under some renewal condition, the maps have polynomial decay of correlations for observables in 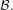${\mathcal{B}}.$ We also provide some general conditions that give aperiodicity for expanding maps in higher dimensional spaces. As applications, we obtain lower bounds for piecewise expanding maps with an indifferent fixed point and for which we also allow non-Markov structure and unbounded distortion. The observables are functions that have bounded variation or satisfy quasi-Hölder conditions and have their support bounded away from the neutral fixed points.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 7 , July 2019 , pp. 1936 - 1970
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J. and Denker, M.. Local limit theorems for partial sums of stationary sequences generated by Gibbs–Markov maps. Stoch. Dyn. 1 (2001), 193–237.Google Scholar
Aaronson, J., Denker, M., Sarig, O. and Zweimüller, R.. Aperiodicity of cocycles and conditional local limit theorems. Stoch. Dyn. 4 (2004), 31–62.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470) . Springer, New York, 1975.Google Scholar
Broise, A.. Transformations dilatantes de l’intervalle et théorèmes limites. Astérisque 238 (1996), 5–110.Google Scholar
Gouëzel, S.. Sharp polynomial estimates for the decay of correlations. Israel J. Math. 139 (2004), 29–65.Google Scholar
Hu, H., Pesin, Ya. and Talitskaya, A.. A volume preserving diffeomorphism with essential coexistence of zero and nonzero Lyapunov exponents. Comm. Math. Phys. 319 (2013), 331–378.Google Scholar
Hu, H.. Decay of correlations for piecewise smooth maps with indifferent fixed points. Ergod. Th. & Dynam. Sys. 24 (2004), 495–524.Google Scholar
Hu, H. and Vaienti, S.. Absolutely continuous invariant measures for nonuniformly expanding maps. Ergod. Th. & Dynam. Sys. 29 (2009), 1185–1215.Google Scholar
Krengel, U.. Ergodic Theorems (de Gruyter Studies in Mathematics, 6) . Walter de Gruyter, Berlin, 1985.Google Scholar
Liverani, C., Saussol, B. and Vaienti, S.. A probabilistic approach to intermittency. Ergod. Th. & Dynam. Sys. 19 (1999), 671–685.Google Scholar
Melbourne, I. and Terhesiu, D.. Decay of correlations for nonuniformly expanding systems with general return times. Ergod. Th. & Dynam. Sys. 34 (2014), 893–918.Google Scholar
Parry, W. and Pollicott, M.. Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérisque 187–188 (1990), 1–268.Google Scholar
Pollicott, M. and Yuri, M.. Statistical properties of maps with indifferent periodic points. Comm. Math. Phys. 217 (2001), 503–520.Google Scholar
Quas, A.. Non-ergodicity for C 1 expanding maps and g-measures. Ergod. Th. & Dynam. Sys. 16 (1996), 531–543 (English summary).Google Scholar
Sarig, O.. Subexponential decay of correlations. Invent. Math. 150 (2002), 629–653.Google Scholar
Saussol, B.. Absolutely continuous invariant measures for multidimensional expanding maps. Israel J. Math. 116 (2000), 223–248.Google Scholar
Yan, J.-A.. A Simple Proof of Two Generalized Borel–Cantelli Lemmas (Lecture Notes in Mathematics, 1874) . Springer, Berlin, 2006, pp. 77–79.Google Scholar
Young, L.-S.. Recurrence times and rates of mixing. Israel J. Math. 110 (1999), 153–188.Google Scholar