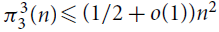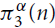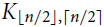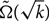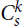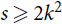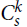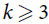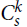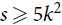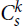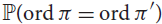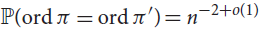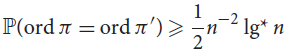Paper
Making Kr+1-free graphs r-partite
- Part of:
-
- Published online by Cambridge University Press:
- 10 November 2020, pp. 609-618
-
- Article
-
- You have access
- Open access
- Export citation
Sharp bounds for decomposing graphs into edges and triangles
- Part of:
-
- Published online by Cambridge University Press:
- 12 October 2020, pp. 271-287
-
- Article
-
- You have access
- Open access
- Export citation
Large complete minors in random subgraphs
- Part of:
-
- Published online by Cambridge University Press:
- 03 December 2020, pp. 619-630
-
- Article
- Export citation
Universal and unavoidable graphs
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2021, pp. 942-955
-
- Article
-
- You have access
- Open access
- Export citation
A counterexample to the Bollobás–Riordan conjectures on sparse graph limits
- Part of:
-
- Published online by Cambridge University Press:
- 27 January 2021, pp. 796-799
-
- Article
- Export citation
Subgraph counts for dense random graphs with specified degrees
- Part of:
-
- Published online by Cambridge University Press:
- 05 November 2020, pp. 460-497
-
- Article
- Export citation
Covering and tiling hypergraphs with tight cycles
- Part of:
-
- Published online by Cambridge University Press:
- 13 October 2020, pp. 288-329
-
- Article
- Export citation
Many disjoint triangles in co-triangle-free graphs
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2020, pp. 153-162
-
- Article
- Export citation
Counting matchings via capacity-preserving operators
- Part of:
-
- Published online by Cambridge University Press:
- 30 April 2021, pp. 956-981
-
- Article
-
- You have access
- Open access
- Export citation
Permutations with equal orders
- Part of:
-
- Published online by Cambridge University Press:
- 27 January 2021, pp. 800-810
-
- Article
- Export citation
Counting Hamilton cycles in Dirac hypergraphs
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2020, pp. 631-653
-
- Article
- Export citation
Turán-type results for intersection graphs of boxes
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2021, pp. 982-987
-
- Article
-
- You have access
- Open access
- Export citation