Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guy, Richard K.
1994.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
105.
Graham, S. W.
1996.
Analytic Number Theory.
p.
431.
Ruzsa, Imre Z.
1999.
Erdős and the Integers.
Journal of Number Theory,
Vol. 79,
Issue. 1,
p.
115.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
159.


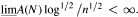 Here it is shown that
Here it is shown that