Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T07:53:43.759Z Has data issue: false hasContentIssue false
  • English
  • Français

Curvature of K-contact Semi-Riemannian Manifolds

Published online by Cambridge University Press:  20 November 2018

Domenico Perrone
Domenico Perrone*
Affiliation:
Universitá del Salento, Dipartimento di Matematica e Fisica “E. De Giorgi”, Via Provinciale Lecce-Arnesano, 73100 Lecce, Italy e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we characterize 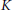$K$-contact semi-Riemannian manifolds and Sasakian semi-Riemannian manifolds in terms of curvature. Moreover, we show that any conformally flat 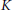$K$-contact semi-Riemannian manifold is Sasakian and of constant sectional curvature 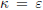$\kappa \,=\,\varepsilon$, where $\varepsilon \,=\,\pm 1$ denotes the causal character of the Reeb vector field. Finally, we give some results about the curvature of a 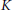$K$-contact Lorentzian manifold.

Keywords

53C5053C2553B30contact semi-Riemannian structuresK-contact structuresconformally flat manifoldsEinstein Lorentzian-Sasaki manifolds
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 2 , 14 June 2014 , pp. 401 - 412
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

Supported by Universitá del Salento and M.I.U.R. (within P.R.I.N. 2010-2011).

References

[1] Baum, H., Twistor and Killing spinors in Lorentzian geometry. In: Global analysis and harmonic analysis (Marseille-Luminy, 1999), Sémin. Congr., 4, Soc. Math. France, Paris, 2000, pp. 35–52.Google Scholar
[2] Blair, D. E., Riemannian geometry of contact and symplectic manifolds. Second ed., Progress in Mathematics, 203, Birkhäuser Boston, Boston, MA, 2010.Google Scholar
[3] Blair, D. E. and Vanhecke, L., Symmetries and ‘-symmetric spaces. Tôhoku Math. J. 39 (1987, no. 3, 373–383.http://dx.doi.org/10.2748/tmj/1178228284 CrossRefGoogle Scholar
[4] Bohle, C., Killing spinors on Lorentzian manifolds. J. Geom. Phys. 45 (2003, no. 3–4, 285–308.http://dx.doi.org/10.1016/S0393-0440(01)00047-X CrossRefGoogle Scholar
[5] Boyer, C. P. and Galicki, K. Sasakian geometry Oxford Mathematical Monographs, Oxford University Press, Oxford, 2008.Google Scholar
[6] Calvaruso, G. and Perrone, D., Contact pseudo-metric manifolds. Differential Geom. Appl. 28 (2010, no. 5, 615–634.http://dx.doi.org/10.1016/j.difgeo.2010.05.006 Google Scholar
[7] Calvaruso, G. and Perrone, D., Erratum to: “ Contact pseudo-metric manifolds, Differential Geom. Appl. 28 (2010), 615–634.”http://dx.doi.org/10.1016/j.difgeo.2010.05.006 Google Scholar
[8] Calvaruso, G. and Perrone, D., H-contact semi-Riemannian manifolds. J. Geom. Phys. 71 (2013, 11–21.http://dx.doi.org/10.1016/j.geomphys.2013.04.001 Google Scholar
[9] Duggal, K. L., Space time manifolds and contact structures. Internat. J. Math. Math. Sci. 13 (1990, no. 3, 545–553.http://dx.doi.org/10.1155/S0161171290000783 Google Scholar
[10] Gomez, R. R., Lorentzian Sasaki-Einstein metrics on connected sums of S2S3. Geom. Dedicata 150 (2011, 249–255.http://dx.doi.org/10.1007/s10711-010-9503-x CrossRefGoogle Scholar
[11] Hatakeyama, Y., Ogawa, Y., and Tanno, S., Some properties of manifolds with contact metric structures. Tohoku Math. J. 15 (1963, 42–48.http://dx.doi.org/10.2748/tmj/1178243868 Google Scholar
[12] Kulkarni, R. S. and F. Raymond, 3-dimensional Lorentz space-forms and Seifert fiber spaces. J. Differential Geom. 21 (1985, no. 2, 231–268.CrossRefGoogle Scholar
[13] Okumura, M., Some remarks on space with a certain contact structure. Tohoku Math. J. 14 (1962, 135–145.http://dx.doi.org/10.2748/tmj/1178244168 CrossRefGoogle Scholar
[14] O’Neill, B., Semi-Riemannian geometry. Pure and Applied Mathematics, 103, Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York, 1983.Google Scholar
[15] Perrone, D., Homogeneous contact Riemannian three-manifolds. Illinois J. Math. 42 (1998, no. 2, 243–256.CrossRefGoogle Scholar
[16] Takahashi, T., Sasakian manifold with pseudo-Riemannian metrics. Tôhoku Math. J. 21 (1969) 271–290.http://dx.doi.org/10.2748/tmj/1178242996 CrossRefGoogle Scholar
[17] Tanno, S., Some transformations on manifolds with almost contact and contact metric structures. II. Tohoku Math. J. 15 (1963) 322–331.http://dx.doi.org/10.2748/tmj/1178243768 Google Scholar
[18] Tanno, S., The topology of contact Riemannian manifolds, Illinois J. Math. 12 (1968, 700–717.10.1215/ijm/1256053971CrossRefGoogle Scholar