Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T03:23:28.622Z Has data issue: false hasContentIssue false
  • English
  • Français

Comparison Geometry With L1-Norms of Ricci Curvature

Published online by Cambridge University Press:  20 November 2018

Jong-Gug Yun
Jong-Gug Yun*
Affiliation:
Department of Mathematics Education, Korea National University of Education, San 7 Darakri Gangnaemyeon, Cheongwongun, Chungbuk 363-791, Korea e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the geometry of manifolds with bounded Ricci curvature in 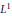${{L}^{1}}$-sense. In particular, we generalize the classical volume comparison theorem to our situation and obtain a generalized sphere theorem.

Keywords

Mean curvatureRicci curvature
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 1 , 01 March 2006 , pp. 152 - 160
Copyright
Copyright © Canadian Mathematical Society 2006

References

[An] Anderson, M. T., Convergence and rigidity of manifolds under Ricci curvature bounds. Invent. Math. 102(1990), 429–445.Google Scholar
[P] Paeng, S.-H., A sphere theorem under a curvature perturbation. II. Kyushu J. Math. 52(1998), 439–454.Google Scholar
[Pe] Petersen, P., Convergence theorems in Riemannian geometry. In: Comparison Geometry, Math. Sci. Res. Inst. Publ. 30, Cambridge, Cambridge University Press, 1997, pp. 167–202.Google Scholar
[PeW] Petersen, P. and Wei, G., Relative volume comparison with integral curvature bounds. Geom. Funct. Anal. 7(1997), 1031–1045.Google Scholar
[S] Sprouse, C., Integral curvature bounds and bounded diamter. Comm. Anal. Geom. 8(2000), 531–543.Google Scholar
[Y1] Yun, J.-G., Mean curvature comparison with L1 -norms of Ricci curvature. Canad. Math. Bull. 47(2004), 314–320.Google Scholar
[Y2] Yun, J.-G., A sphere theorem with integral curvature bounds. Kyushu J. Math. 56(2002), 225–234.Google Scholar
[Z] Zhu, S., The comparison geometry of Ricci curvature. In: Comparison Geometry, Math. Sci. Res. Inst. Publ. 30, Cambridge, Cambridge University Press, 1997, pp. 221–262.Google Scholar